2.1.3. Расчет ускорений

По аналогии с планом скоростей при помощи плана ускорений можно найти ускорения любых точек механизма. При построении планов ускорений надо использовать их свойства:

векторы, выходящие из полюса, означают абсолютные ускорения соответствующих точек в масштабе плана ускорений. Точки на плане ускорений, соответствующие точкам с ускорениями, разными нулю, располагаются в полюсе;

векторы, соединяющие концы векторов абсолютных ускорений, выражают полные относительные ускорения.

Расчет ускорений проводится для двух положений рабочего хода механизма, в которых сила полезного сопротивления не равна нулю. Ускорения определяются подобно скоростям, расчет которых был проделан выше (п. 2.1.2). В данном курсовом проекте рассчитываются линейные и угловые ускорения в положениях механизма №1 и №5.

Первоначально определим ускорение точки А кривошипа. Оно является постоянным и равно произведению квадрата угловой скорости кривошипа на его длину[1,3]:

(2.4)

м/с².

Нахождение ускорений будем производить методом планов, для этого запишем векторное уравнение ускорения точки В[1,3]:

(2.5)

где и -векторы нормальной и тангенциальной составляющей абсолютного ускорения звена АВ соответственно.

Решим уравнение (2.5) графически. Для этого примем масштабный коэффициент плана ускорений , равный:

где мм.

Строим план ускорений согласно направлению векторов:

- направлен из по направляющей от точки А в точку О₁;

- направлен по направляющей из точки В в точку А;

- направлен по линии перпендикулярной звену АВ;

- направление задается направляющей t – t.

Определим значение нормальной составляющей абсолютного ускорения звена АВ [1,3]:

, (2.6)

м/с².

Для построения плана ускорений:

выбираем полюс р_а ;
строим вектор ускорения точки А;
из конца вектора строим луч параллельный звену АВ, и на этом луче откладываем отрезок an равный: ;
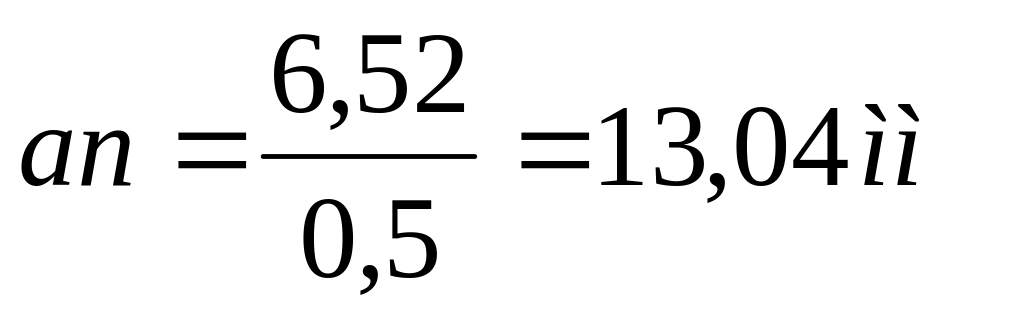
через точку n проводим прямую перпендикулярную АВ, отмечаем точку пересечения ее с направляющей t-t – точка b;
отрезок р_аb – изображает ускорение точки В на плане ускорений.