Расчеты и выводы Контрольные вопросы.

1. Сформулируйте I начало термодинамики по отношению к процессам теплообмена; к процессам, протекающим в калориметре.

2. Какая из предложенных в §3, пункт 1 ситуаций для исследования Вам кажется наиболее приемлемой (самой интересной!)?

3. Назовите возможные систематические погрешности, которые могут вести к искажению результатов полученных в предлагаемых экспериментах.

4. Приведите примеры систем, у которых не монотонно меняются физические характеристики от времени.

Литература:

1. Р.В. Телеснин. Молекулярная физика. М.: Высшая школа, 1973, §64 (Закон охлаждения Ньютона); §65 (Конвекция). !*Обязательно прочесть.

2. В.Ф. Яковлев. Курс физики (теплота и молекулярная физика) М. 1976. §15 (Измерение теплоемкости), §16 (Внутренняя энергия как функция состояния).

3. Энциклопедия и физические энциклопедические словари на слова: теплообмен и теплоотдача.

Определение удельной теплоемкости металлов

Удельной теплоемкостью однородной материальной среды принято называть то количество теплоты, которое необходимо сообщить единице массы системы, чтобы изменить её температуру на единицу.

Для конденсированных сред в большинстве ситуаций (исключая область близкую к критическому состоянию жидкости) мало значимо в сравнении с изменением внутренней энергии Du_х. Следовательно, корректно считать:

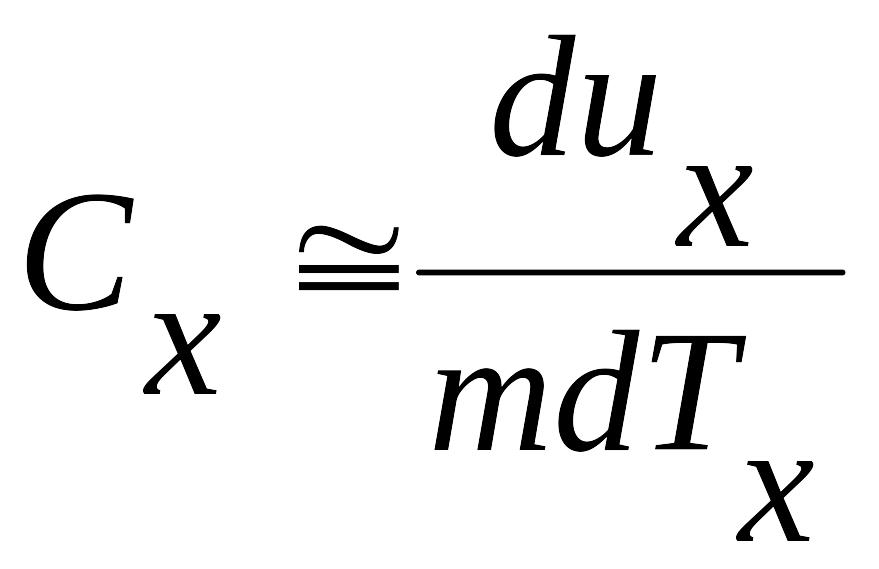
Сравнивая С_V и С_p таких сред, важно отметить, что

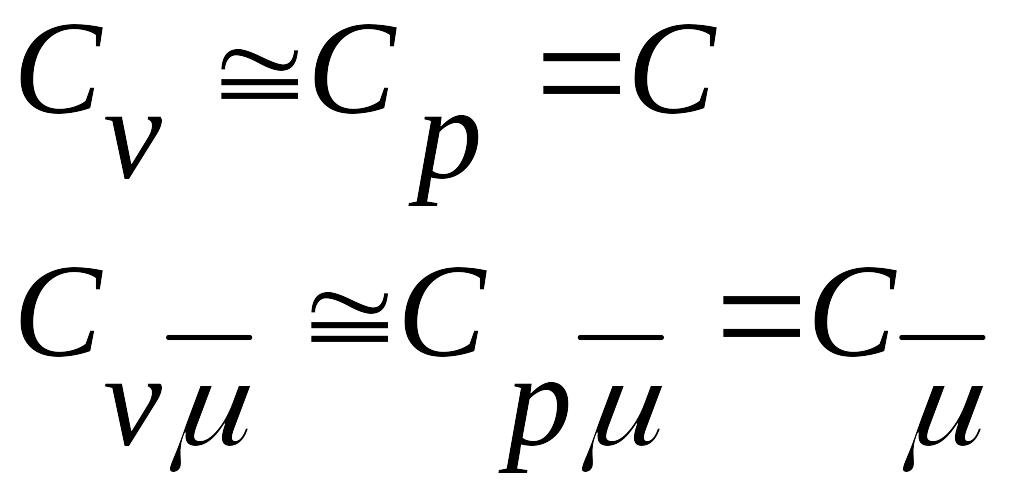
1. Введение: опыт и модельно-теоретические представления о теплоемкости атомных и ионных кристаллов.

§1. Закон Дюлонга-Пти.

К 1819 году французскими учеными Дюлонгом и Пти лабораторно-опытным путем был установлен закон о теплоемкости металлов в твердой фазе: произведение удельной теплоемкости и атомного веса простых твердых тел (атомных кристаллов металлов) является величиной почти одинаковой (таблица 1).

Таблица 1.

В-во характеристика		(сталь)
С Сm	896 24,2	460 25,7	395 25,1	234 25,3	126 26,1	230 27,3

Теоретически обосновать этот закон о молярной теплоемкости атомных кристаллов (металлов и ионных структур типа NaCl, LiF, CaCl₂) удалось только с учетом представлений развитых Л. Больцманом о средней энергии, приходящейся на различные степени свободы хаотического движения микрочастиц (поступательное – пхдм; вращательное – вхдм; колебательное – кхдм). В классическом приближении, когда энергетический спектр разрешенных (дозволенных) значений энергии непрерывен, средняя энергия на одну степень свободы:

• п.х.д.м. и в.х.д.м. -

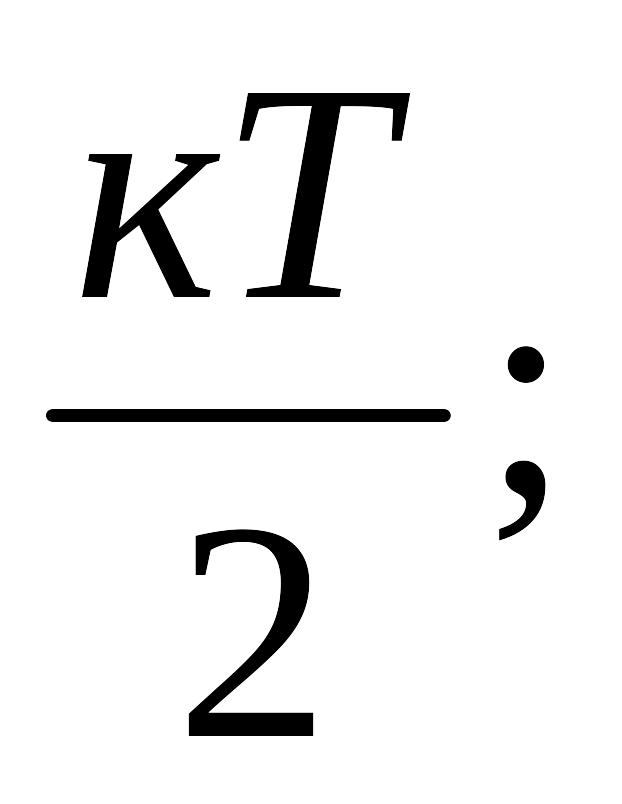
• к.х.д.м. – кТ = (

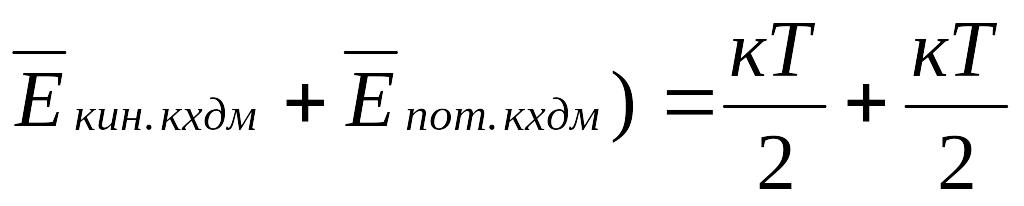
В соответствии с классическим приближением ионы металла колеблются в узлах кристаллической решетки, а, обладая тремя степенями свободы, характеризуются средним значением .

(1.2)

Именно вблизи этого значения и находятся экспериментальные данные, приведенные в таблице 1 и подтверждающие закон Дюлонга – Пти.

*Заключение, аналогичное (1.1) и (1.2) можно сделать и для ионных твердых тел (кристаллы NaCl, LiF, CaCl₂ и др.), если учесть, что каждый ион структуры реализует три степени свободы:

• для двухатомных кристаллов

• для трехатомных

** Об ожидаемом вкладе свободных электронов металлов в удельную теплоемкость.

В классическом приближении электронный газ металлов (свободные электроны) должен давать существенный вклад в теплоемкость. Если допустить, что каждый атом дает один свободный электрон (строго соблюдается в щелочных металлах Na, К, Cs и др.), то внутренняя энергия моля металла должна быть:

(1.3)

; ( - ожидаемая электронная составляющая теплоемкости; - ожидаемая решеточная составляющая).

Однако реальность не подтверждает такого вклада электронов в теплоемкость металлов. В широком температурном интервале этот вклад мал. Только при высоких температурах (близких или превышающих тысячу К) вклад этот становится значимым.