§2. Объяснение теплового расширения.

С точки зрения молекулярно-кинетической теории тепловое расширение конденсированных сред может быть обусловлено только изменением среднего расстояния между структурными микрочастицами (молекулами, атомами, ионами). В свою очередь среднее расстояние между структурными микрочастицами определяется особенностями их взаимодействия и характером хаотического колебательного движения.

Взаимодействие между структурными микрочастицами конденсированной среды всегда имеет две составляющие: притяжение и отталкивание. Разноименные заряды притягиваются (электроны электронной оболочки одной микрочастицы притягиваются к ядру другой и наоборот), а одноименные – отталкиваются (взаимодействие электронных оболочек друг с другом и ядер друг с другом). Итоговое описание взаимодействия двух микрочастиц может быть представлено:

,

Где: r  расстояние между микрочастицами;

А, В, и m  некоторые константы, характерные для типа связи данной конденсированной среды.

а = nА; в = mВ. Первое слагаемое в выражениях (1) и (2) соответствует проявлению сил притяжения, стремящихся уменьшить “r” между частицами ( и противонаправлены); второе – силам отталкивания, сонаправленным с “r”.

Показатели степени “m” и “n” всегда положительные, больше единицы и m > n.

Для ковалентного типа связи атомов в молекуле m = 8, n = 6; (например, в молекулах N₂, H₂, O₂) для полярного взаимодействия m = 68, n = 1 (например, в молекулах NaCl, LiF).

Взаимодействие структурных микрочастиц (молекул, атомов, ионов) в конденсированных средах осуществляется, реализуя такие виды связи:

1. ионную;

2. ковалентную;

3. дипольное взаимодействие молекул с собственными дипольными моментами (например, у молекул воды – Н₂О), взаимодействие молекул с диполями, появляющимися при движении валентных электронов электронной оболочки. Это взаимодействие еще называют молекулярным или ван-дер-ваальсовским (например: между молекулами “сухого льда” – СО₂ в жидком и твердом азоте, кислороде, водороде);

4. Металлический тип связи между положительными ионами жидкости или твердого тела, осуществляемый свободными электронами (рис.1).

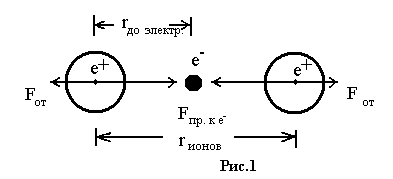
Так проявляется эффект притяжения;

5. водородный тип связи, характерный для водородосодержащих молекул.

В реальных конденсированных средах, как правило, реализуется смешанный тип связи, при котором реализуется несколько механизмов взаимодействия структурных микрочастиц. Для описания такого взаимодействия обычно пользуются приближением Леннарта-Джонса с показателями: n = 6, m =8.

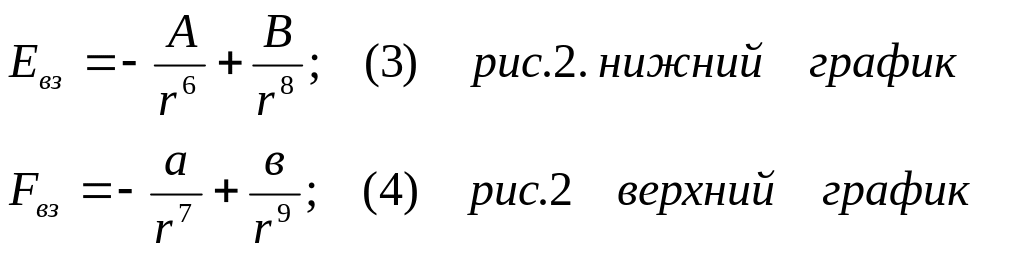
Графически эти функциональные зависимости можно достаточно просто представить, если начало системы отсчета связать с центром одной из взаимодействующих молекул (в дальнейшем эта молекула обозначена цифрой 1).

Воспользуемся графической и аналитической зависимостями Е_вз(r) для объяснения теплового расширения конденсированных сред. С этой целью введем дополнительную систему координат, связанную с минимумом потенциальной энергии взаимодействия (рис.3). Учтем при этом и то важное обстоятельство, что частицы среды в основном осуществляют колебательное хаотическое движение.

В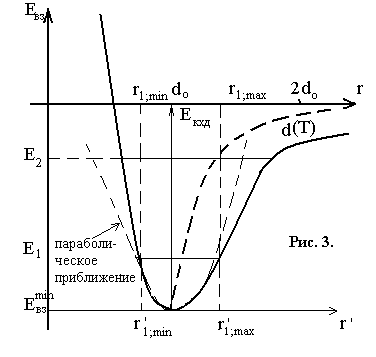 выбранной системе отсчета Е_кхд(r^’) изоэнергетические состояния колеблющейся частицы будут изображаться линиями параллельными осям координат r^’ и r. В классическом приближении по теореме Л. Больцмана средняя энергия на одну степень свободы колебательного хаотического движения:

.

При Е₁ пределы колебания будут от r_{1; min} до r_1;max ( Причем смещение вправо от всегда будет несколько больше (колебания асимметричны в асимметричной “потенциальной яме”). Большему амплитудному смещению на удавление микрочастиц будет соответствовать и большее время пребывания частицы в этих состояниях, чем в состояниях на сближение.

Среднее расстояние между колеблющимися микрочастицами (атомами, ионами, молекулами) будет определяться интегралом:

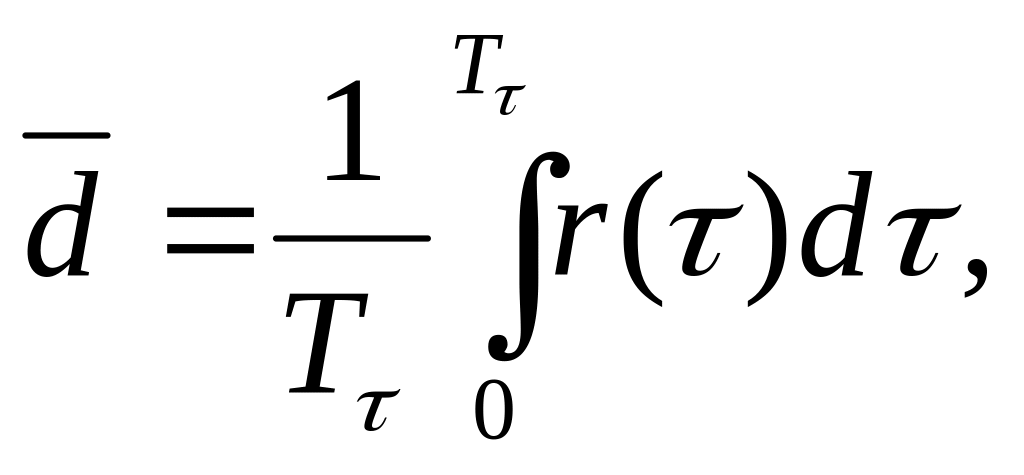
 - время; Т_ - период колебаний. Очевидно, что при асимметричных колебаниях . Чем выше температура, тем больше энергия колебательного движения (Е₂>Е₁), возрастает и фактор асимметрии. Следовательно, с ростом температуры увеличивается , что и обуславливает тепловое расширение конденсированных сред. На рисунке эта зависимость изображена пунктирной линией.

!! В дополнение к изложенному объяснению следует понять и такие важные обстоятельства:

1. При низких температурах (Т0 К) асимметрия “потенциальной ямы” незначительна. А это значит, что при Т0 К коэффициенты теплового расширения уменьшаются и в пределе становится равным 0. (Такой вывод находится в полном соответствии с III началом термодинамики, описывающим свойства систем вблизи абсолютного нуля температур);

2. При колебаниях структурных микрочастиц, когда амплитудное смещение вправо становится больше, чем “r” соответствующее минимуму F_вз(r) (r₀1,14 d₀) асимметрия колебаний резко начинает возрастать. В реальной практике это может соответствовать фазовому переходу “твердое тело-жидкость” (плавлению). У жидкостей коэффициент объемного расширения значительно больше и он растает с температурой.