Федеральное агентство по образованию

Поморский государственный университет имени М.В.Ломоносова

Кафедра общей физики

Лабораторный практикум

по молекулярной физике

Часть III

Архангельск

САФУ 2011

Методические рекомендации для студентов 1-го курса физического факультета ПГУ.

П о с в я щ а ю т с я

сыну и отцу физико-математического факультета

Дубровину

Павлу Васильевичу

(27 августа 1912 – 30 июля 1975)

Автор-составитель и редактор методических рекомендаций:

доцент кафедры общей физики Колпачников Г.Н.

Кафедра общей физики ПГУ имени М.В. Ломоносова.

Лаборатория механики и молекулярной физики.

Г руппа __________ Фамилия И.О. студента ______________

Содержание

Стр

Периодическая система элементов 4

Формулы приближенных вычислений, тригонометрические формулы 5

Лабораторный практикум:

1. Изучение явления теплоотдачи 6

2. Определение удельной теплоемкости металлов 13

3. Диаграммы плавкости металлов и их сплавов 27

4. Определение средних значений коэффициентов линейного 40

и объемного расширения конденсированных сред

5. Газовый термометр: градуировка и измерение температуры 50

Автор-составитель искренне благодарен тем, кто принимал участие в постановке и модернизации работ практикума, в подготовке настоящих методических рекомендаций: Лазаревой О.В., Абикулову И.В., Тюкину Д.А, Михайлову И.Н, Орлову А.В. и др

Формулы для приближенных вычислений.

Если а << 1, то в первом приближении можно принять:

Если угол  мал ( < 5^о или  < 0,1 рад) и выражен в радианах, то в первом приближении можно принять:

Тригонометрические формулы.

sin (x + y) = sin x cos y + sin y cos x sin (x – y) = sin x cos y – sin y cos x

cos (x + y) = cos x cos y – sin x sin y cos (x – y) = cos x cos y + sin x sin y

sin 2x = 2sin x cos y cos 2x = cos²x – sin²x

sin²x = ½(1 – cos 2x) cos²x = ½(1+cos 2x)

sin аx sin bx = ½ cos (a – b)x – ½ cos (a+b)x

sin ax cos bx = ½ sin (a + b)x + ½ sin (a – b)x

Изучение явления теплоотдачи

Цель работы: методом прямых измерений получить зависимость температуры воды, находящейся в сосуде от времени (t^оС(t)) в условиях теплообмена (разного) с окружающей средой; проанализировать полученные данные, выявив аналитическую зависимость температуры от времени.

§1.Элементы теории теплоотдачи

Под теплоотдачей понимают процесс теплообмена между поверхностью нагретого (охлажденного) тела и окружающей средой. Возможные механизмы теплоотдачи: теплопроводность, конвекция и тепловое излучение. Так как в нашей ситуации температура нагретой воды и окружающей среды максимально отличаются только на несколько десятков градусов, то механизм теплопотерь за счет излучения существенной роли не играет. Меняя конвекционные потоки или теплопроводность окружающей среды, можно изменять и скорость процесса теплоотдачи.

Пусть остывающее тело, имеющее площадь поверхности, через которую происходит теплообмен, S и температуру t, находится в среде с температурой t_о(t > t_о).

Теплоемкость окружающей среды, как правило, многократно превосходит теплоемкость остывающего объекта. Поэтому есть основание полагать, что t_о во время такого эксперимента остается постоянной. При длительном эксперименте контроль за постоянством t_о необходим. Если же t_о несколько меняется, то необходимо за температуру среды взять ее среднее значение.

Элементарный процесс теплообмена между остывающим телом и средой можно описать, опираясь на первое \начало термодинамики, двояко:

1. Как процесс понижения температуры объекта исследования. Полагая, что теплоемкость исследуемого тела есть некоторая постоянная величина. Количество внутренней энергии, отданное телом:

(1)

где q – теплоемкость объекта;

знак “-” указывает на то, что процесс теплообмена сопровождается понижением температуры.

2. Как процесс теплоотдачи, когда dQ можно представить в виде:

(2)

где:

α – средний коэффициент теплоотдачи поверхности объекта остывания, имеющего площадь S;

время dt;

t – температура тела;

– температура окружающей среды.

Приравняв правые части равенств (1) и (2), получим дифференциальное уравнение для процесса остывания:

(3^’)

Проведя разделение переменных, и обозначив .

Перейдем от (3^’) к уравнению 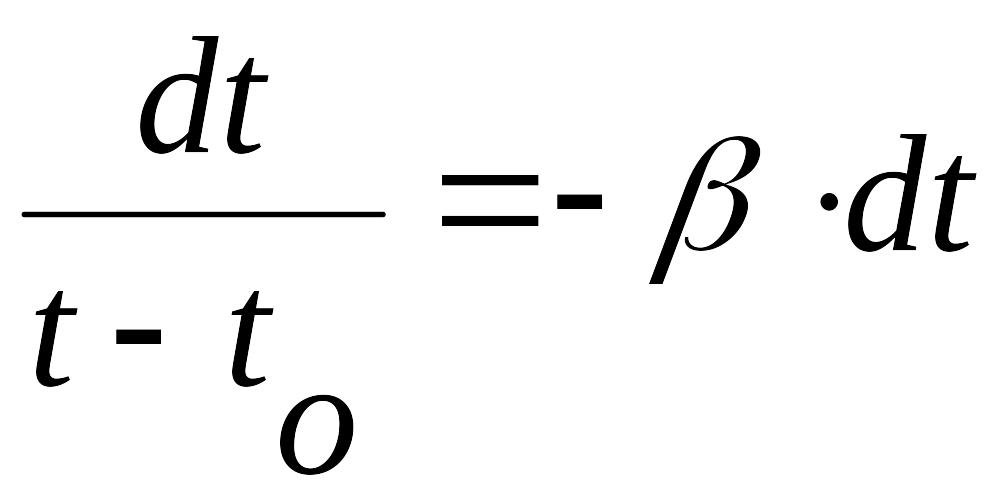(3):

(3)

Решение дифференциального уравнения (3) с учетом начальных условий (t = 0 Þ t_t = t_н – начальная температура остывающего тела) будем иметь:

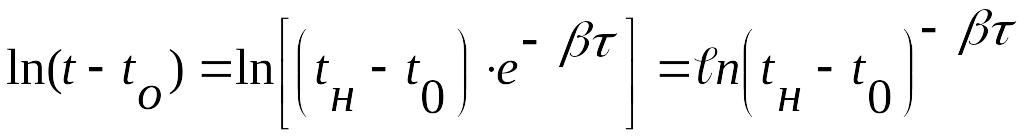(4)

(5)

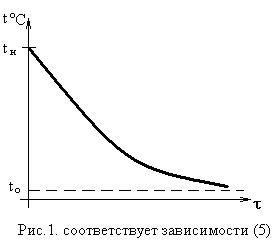
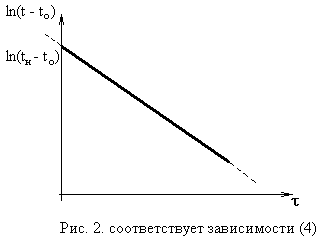
В соответствии с оговоренными условиями температура охлаждаемого объекта должна со временем экспоненциально уменьшаться от начальной температуры t_н(t = 0), стремясь достичь t_о (рис. 1 и 2).

Очевидно, что полученная теоретически фундаментальная зависимость t(t) графически наилучшим образом выявляется, если она представлена в координатах ln(t – t_о) от t - линейная убывающая функция.