4.3. По натеканию воздуха через капилляр в разреженную среду.

Э тот метод предусматривает измерение меняющейся разности давлений Δp на концах капилляра в течение конкретного опыта. Он проще с точки зрения создания и измерения разности давлений между атмосферным давлением и давлением в сосуде 2.

Первичная разность давлений на концах капилляра 1 создаётся насосом Шинца 5 при открытом кране 6. Клапан-наигольник 4 при этом закрыт.

Будьте внимательны: не допускайте разности давлений больше, чем это возможно для показаний манометра.

Перед тем, как начать эксперимент, кран 6 перекрывают. Натекание воздуха будет происходить в установку, когда наигольница снята. Разность давлений на концах шприца с течением времени будет убывать. Фиксируйте одновременно показание манометра и секундомера.

Вывод рабочей формулы.

Пусть за время d объем втекшего в сосуд газа (воздуха) dV. Тогда по формуле Пуазейля (3.1) его можно выразить:

где: Р = Р_о – Р, Р_о – давление атмосферное; Р – давление воздуха в сосуде.

Масса этого газа:

_Г – плотность воздуха.

Разность давлений по уравнению Клапейрона-Менделеева может быть найдена:

П одставив в уравнение (3.6) р из (3.7) будем иметь:

Преобразуем это дифференциальное равенство к виду с разделенными переменными:

Проинтегрируем левую и правую части равенства (3.8):

Придав, полученной зависимости экспоненциальный характер, и учтя, что

обозначено за С_о, получим:

(3.9)

Зависимость (3.9) указывает на то, что разность давлений в сосуде и окружающей среде будет в процессе проталкивания воздуха через капилляр (иглу шприца) экспоненциально убывать со временем.

Данные о разности давлений в сосуде и атмосфере легко манометрически измеряются P₀ – P = р = gh, где h – разность уровней манометрической жидкости с плотностью .

Если разность уровней h измерить в момент запуска секундомера (₁=0) и по истечению времени , то данных об h₁ и h₂ будет достаточно для определения , если известны значения объема сосуда – V, характеристики капилляра, молярная масса воздуха -  и температуру окружающей среды – Т.

Действительно, после логарифмирования (3.9) для двух состояний воздуха в сосуде имеем:

- для ₁=0: (I)

- для ₂: (II)

В ычтем из равенства (I) равенство (II) и учтем, что ₂ - ₁ = :

Это позволяет для коэффициента вязкости получить аналитическое выражение (3.10) через экспериментально измеряемые величины:

(3.10)

Измерения и обработка результатов.

1. Ознакомьтесь с установкой.

2. При закрытой игле откачайте воздух из сосуда 2 с помощью насоса Шинца таким образом, чтобы разность давлений была близка к максимальной. Нижний и верхний уровни манометра не должны доходить до предельного уровня на (710) см.

3. Убедившись, что разность уровней жидкости в коленах манометра установилась (h₁ = const), измерьте её с точностью, которую допускает линейка.

4. Предлагаемый метод не требует отбора интервала падения давления в системе (h₂ может быть, вообще говоря, любым). Однако, давление в системе не следует сводить к значениям, близким к нулю: h₂ = (710) см.

5. Измерения проведите не менее 5 раз. Данные занесите в таблицы. Проведите расчет _сл, h_пр и полной относительной погрешности .

• Объём сосуда V = (25,4 ± 0,1) л

• Диаметр капилляра d = (0,52 ± 0,01) мм

• Длина капилляра l = (4,5 ± 0,1) см

Таблица постоянных данных для установки и условий эксперимента.

		r м	r м	 кг/м3		g м/с2	g	 м	 м	 кг/мольК	

V	V	P0	P0	Т; К	Т; К

Таблица данных о многократных измерениях.

,
, с
, Па·с

Примечания:

1. Как уже отмечалось, в нашем случае течение воздуха происходит по достаточно короткому капилляру и разность давлений ΔP много меньше атмосферного давления P_0, а поэтому есть основание считать газ, проталкиваемый через капилляр, несжимаемым.

2. Ламинарность течения воздуха по капилляру можно (и нужно!) оценить, имея уже полученные данные, по критерию Рейнольдса: R_e = ( 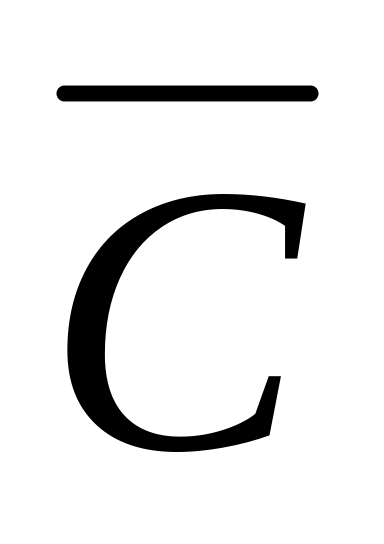rρ_возд)/η ,

где: - среднее значение скорости течения воздуха по сечению капилляра =V_ /(r² )

(Vτ - объём воздуха протекшего через капилляр за время τ);

Таким образом, если R_е<1000, то течение газа через капилляр можно считать ламинарным.

Проверьте правомерность ваших предыдущих расчётов по критерию Рейнольдса и приступайте к оценке средних значений и d_эф молекул воздуха в условиях проведения эксперимента.