§2. Модель явления внутреннего трения в идеальном газе.

Очевидно, что механизм явлений переноса в идеальном газе один и тот же и он обусловлен тепловым хаотическим движением молекул. Именно этот переход молекул из одного слоя в другой и сопровождается передачей импульса направленного движения от слоя к слою.

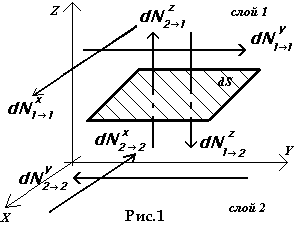1. Рассмотрим тепловое движение молекул в приближении, что все молекулы разделились на 6 одинаковых потоков, параллельных координатным осям (приближение Джоуля). Таким образом, 1/6 всех молекул будет двигаться снизу – вверх, 1/6 – сверху – вниз. Только молекулы этих двух потоков и будут участвовать в передаче количества движения (импульса).

2. Количество молекул, переходящих через площадку dS за время d

из слоя 1 в слой 2:

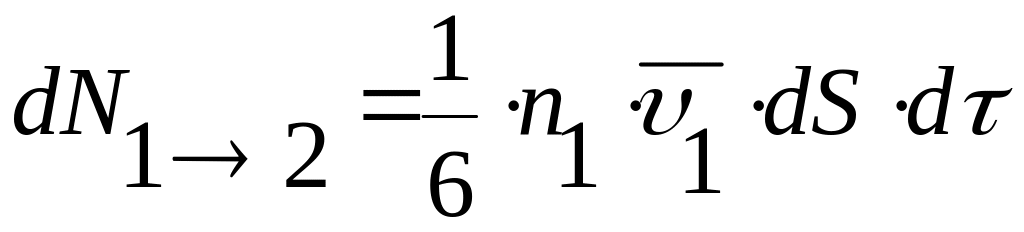
из слоя 2 в слой 1:

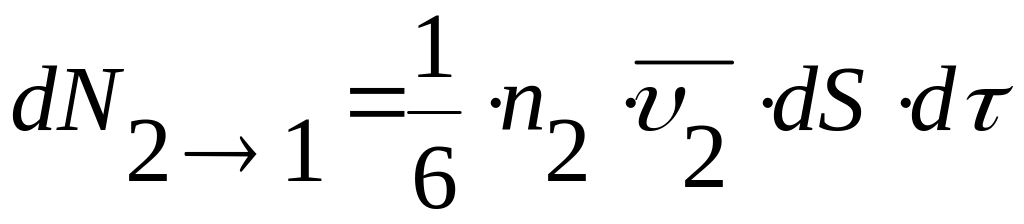
Так как накопления молекул нигде нет, то

где: n и - характеристики газовой среды в месте нахождения площадки dS.

- средняя скорость теплового движения молекул.

4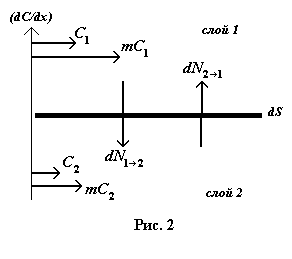 . Молекулы различных слоев движутся с разными скоростями направленного движения. Допустим , что C₁ > С₂. Тогда итоговая потеря импульса слоем 1 через площадку dS за время d будет равен:

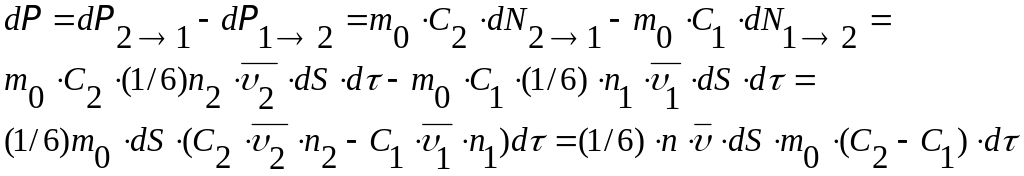
1. Для фиксации скоростей С₁ и С₂ учтём, что С₁ и С₂ надо относить к тем молекулам, которые переходят через площадку dS после последнего столкновения. Т.к. последнее столкновение разные молекулы испытывают на разных расстояниях от площадки dS, то в усредненном варианте это расстояние равно средней длине свободного пробега (рис. 3).

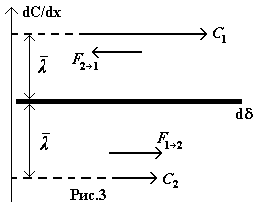« -» указывает на то, что С₂ – С ₁ < 0 и характеристики (dC/dx)>0 и >0

6. Слой с большей скоростью направленного движения ускоряет более медленный слой и наоборот.

С другой стороны по закону Ньютона,

Следовательно: (2.1)

Экспериментальное определение коэффициента внутреннего трения η в газовых средах (в воздухе)

Все установки, предлагаемые в лабораторном практикуме для определения коэффициента вязкости и других характеристик воздуха, основаны на проталкивании газовой среды через капилляр (иглу шприца) с фиксированными значениями длины и сечения путем создания на концах иглы разности давлений - Р.

§3. Вывод рабочей формулы (формулы Пуазейля) для определения коэффициента вязкости .

П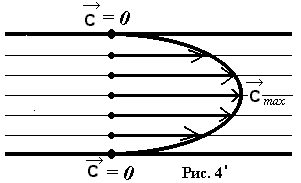 ри установившемся ламинарном течении скорости движения бесконечно тонких слоёв воздуха, на различных расстояниях от оси капилляра, различны.

Е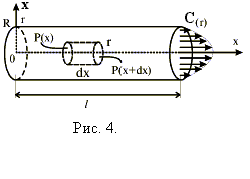 сли считать, что для слоя, прилегающего к стенкам капилляра, имеет место явление прилипания, то скорость этого слоя равна нулю. Наибольшая скорость будет на осевой линии капилляра (рис.4^’). Вследствие различия скоростей слоёв между ними возникнут силы внутреннего трения. При установившемся движении сила вязкости, действующая на элементарный цилиндрический объём и приложенная к боковой поверхности цилиндра, уравновешивается разностью сил давления, действующих на основания этого выделенного цилиндра.

З апишем уравнение установившегося равномерного протекания несжимаемой вязкой среды по трубке длинной dx и радиусом r.

О тметим, что равнодействующая сил давления направлена по потоку (вдоль оси x), а сила вязкого трения, приложенная к боковой поверхности цилиндрического объема - против потока. Произведя сокращение и разделив на dx, получаем для установившегося направленного движения:

Величина градиента давления dр/dx не зависит от радиуса r, т.к. давление p = p(x) и в поперечном сечении (x = const) не меняется. Это позволяет решить дифференциальное уравнение, сведя его к виду:

У равнение (3.2) позволяет рассчитать распределение скоростей, полагая, что у стенок трубы эта скорость равна нулю. После интегрирования получаем:

Параболическое распределение скоростей графически изображено на рисунках 4’ и 4 данного параграфа.

При установившемся ламинарном течении несжимаемой вязкой среды по капилляру радиуса r ее объем, протекший через сечение будет определяться формулой Пуазейля:

(3.4)

где:

V _ -объём воздуха, протекающего через сечение капилляра за время τ;

η- коэффициент динамической вязкости;

Δp- разность давлений в начале и в конце капилляра;

l- длина капилляра.

Так как в нашем случае измерение проводятся при небольших разностях давлений на концах капилляра, то течение воздуха по капилляру можно считать ламинарным, а газ несжимаемым ( ). Следовательно, к расчётам V_ и  применима формула Пуазейля.

(3.5^’)

Учтя, что р = р₁ – р₂ = gh, где ρ - плотность манометрической жидкости (в учебных лабораториях обычно используется вода), будем иметь:

(3.5)