
- •Часть I
- •Содержание.
- •Лабораторный практикум:
- •Измерения, их погрешности и обработка результатов измерений.
- •Обработка результатов прямых измерений.
- •II. Значащие и запасные цифры в числах и вычислительные операции с этими числами.
- •III. Обработка и представление результатов косвенных измерений.
- •Некоторые числа и физические константы, используемые при расчетах:
- •Формулы для приближенных вычислений
- •Некоторые математические формулы и соотношения:
- •Тригонометрические формулы
- •Формулы дифференциального и интегрального исчислений
- •Определение удельной теплоты плавления льда калориметрическим методом
- •§1. Характеристики процессов теплообмена.
- •§2. Энергетика фазовых переходов при плавлении и кристаллизации.
- •§3. Экспериментальные закономерности для процессов плавления.
- •§4. Общие принципы калориметрических измерений.
- •§5. Определение удельной теплоты плавления льда при атмосферном давлении (определяется по барометру и пересчитывается в Па с учетом 3х значащих цифр).
- •Расчеты.
- •Контрольные вопросы:
- •Литература:
- •Теоретическая часть:
- •§1. Основные понятия.
- •§2. Законы изопроцессов и уравнение Клапейрона (уравнение для любых реальных идеальных газов).
- •§3. Уравнение состояния однокомпонентного идеального газа – уравнение Клапейрона-Менделеева.
- •§4. Физический смысл универсальной газовой постоянной.
- •§5. Давление. Разность давлений. Измерение давления и разности давлений.
- •I. Экспериментальное определение r методом откачивание воздуха из сосуда определенного объема.
- •II. Определение r методом впрыскивания в сосуд с воздухом легко испаряющейся жидкости.
- •Результаты эксперимента и обработки данных представлены в таблице №2.
- •Контрольные вопросы:
- •Теоретическое введение
- •§1. Внутренняя энергия идеального газа
- •§3. О воздухе.
- •§4. Адиабатный и политропический процессы.
- •§4А. Постройте графики изопроцессов, включая адиабатный, в различных координатах:
- •§4Б. Политропические процессы при различных “n” и их графическое представление.
- •§6. Экспериментальное определение для воздуха.
- •1. Описание метода Клемана и Дезорма (приближение Клемана-Дезорма).
- •2. Измерения и обработка результатов.
- •Контрольные вопросы:
- •Литература:
- •Определение коэффициента внутреннего трения воздуха.
- •Явления переноса
- •§ 1. Феноменологическое описание явлений переноса
- •§2. Модель явления внутреннего трения в идеальном газе.
- •Экспериментальное определение коэффициента внутреннего трения η в газовых средах (в воздухе)
- •§3. Вывод рабочей формулы (формулы Пуазейля) для определения коэффициента вязкости .
- •§4. Методы экспериментального определения и обработка результатов измерений.
- •4.1. По методу натекания воздуха из атмосферы через капилляр в разряженную среду.
- •4.2. По выталкиванию воздуха через капилляр в атмосферу.
- •Измерения и обработка данных для первого и второго предлагаемых методов.
- •4.3. По натеканию воздуха через капилляр в разреженную среду.
- •§5. Расчёт средней длины свободного пробега ( ) и эффективного диаметра молекулы воздуха
- •Контрольные вопросы:
§3. О воздухе.
Сухой воздух содержит: 78,1 % азота – N2; 21,0 % кислорода – О2; 0,94 % инертных газов – He, Ne и др.; 0,03 % СО2 и в небольшом количестве других газов.
Средняя молярная масса воздуха:
![]()
Среднее число степеней свободы молекул воздуха в широком температурном интервале практически совпадает с числом степеней свободы у жестких 2-х атомных молекул (их в воздухе чуть более 99 %).
![]()
В приведенных соотношениях:
m – масса рассматриваемой системы,
- средняя молярная масса смеси газов,
ni – число молей (количество вещества) i –го газа;
![]() -
общее количество вещества в системе,
выраженное в молях;
-
общее количество вещества в системе,
выраженное в молях;
ii – число степеней свободы у молекул i – го газа;
![]() -
среднее число степеней свободы для
молекул смеси газов (многокомпонентной
газовой системы).
-
среднее число степеней свободы для
молекул смеси газов (многокомпонентной
газовой системы).
Средние значения молярных и удельных теплоемкостей:
![]()
![]()
Тогда в модельном представлении о воздухе, как идеальном газе из жестких молекул, отношение изобарической и изохорической теплоемкостей, обозначаемое g равно:
![]()
Реальный воздух влажный. Он содержит пары воды. Молекулы воды в газообразном состоянии, как пространственные жесткие, обладают 6-ю степенями свободы. При температуре 25оС и влажности 65 % доля молекул воды в воздухе не превышает 1,0 %. В отношении среднего значения степеней свободы у молекул такого воздуха это своеобразная компенсация присутствия в нем примерно такой же доли одноатомных молекул инертных газов (i = 3). Поэтому водяной пар, не конденсирующийся в эксперименте, дополнительно приближает среднее число степеней свободы молекул воздуха к пяти (
 ).
).
§4. Адиабатный и политропический процессы.
Адиабатными или изоэнтропийными процессами называют такие, которые протекают в системах, не обменивающихся с объектами, в систему не входящими, внутренней энергией, т.е. в системах теплоизолированных:
![]()
Работа системы в адиабатном (изоэнтропийном) процессе совершается за счет убыли ее внутренней энергии. Если речь идет об идеальном газе, то:
![]()
К политропическим процессам относят те, для которых теплоемкость системы (в том числе, молярная и удельная) остаются величинами постоянными. Очевидно, что к таким процессам относятся все изопроцессы, включая изоэнтропийный (адиабатный).
Получим уравнения адиабатного и политропического процессов для идеального газа, следуя оговоренным выше условиям теплообмена.
адиабатный процесс
Решение полученного дифференциального уравнения довольно просто.
Воспользовавшись УС идеального газа легко получить уравнение этого процесса и в других координатах:
|
политропический процесс m = m ; Cn = const; Cnm = const
По УС идеального газа
Решение дифференциального уравнения (а) аналогично решению дифференциального уравнения (1) в адиабатном процессе, если
n – показатель политропического процесса (показатель политропы).
В соответствии с (б)
|


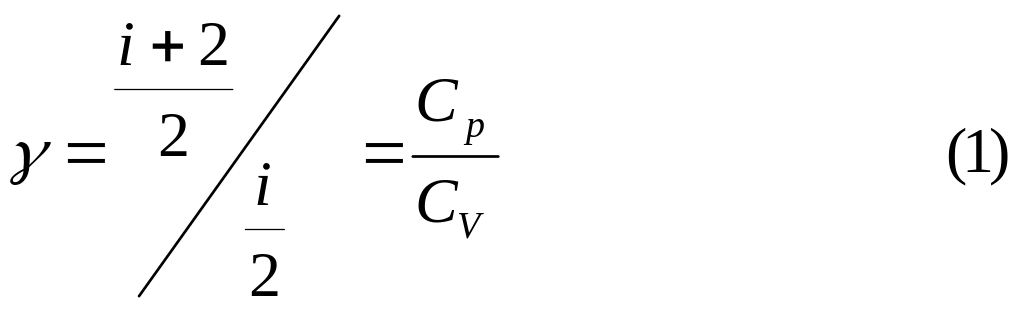
 (в)
(в)