Контрольные вопросы:

1. Графики изопроцессов с реальным идеальным газом в координатах PV, P,T (P, t^оC); V,T (V,t^оC).

2. Построить поверхность, соответствующую УС идеального газа определенной массы m в координатах PVT.

3. Систематические погрешности в предлагаемых методах определения R и возможные методы уменьшения их влияния.

ЛИТЕРАТУРА:

1. Кикоин А. К., Кикоин И. К. Молекулярная физика. М., «Наука», 1976.

2. Сивухин Д. В. Общей курс физики, т. II. М., 1975, §7, 8, 9.

3. Штрауф Е. А. Молекулярная физика. Л.,1949, стр. 138-147.

4. Шубин А. С. Курс общей физики. М., «Высшая школа»,1976.

5. Яковлев В. Ф. Курс физики. Теплота и молекулярная физика. М., «Просвещение», 1976, §7, 8, 9, 10.

Определение отношения изобарической и изохорической теплоемкостей воздуха методом

Клемана и Дезорма.

Цель работы: экспериментально, используя метод Клемана и Дезорма, определить отношение теплоемкостей в изобарическом и изохорическом процессах для воздуха; сравнить полученный результат с ожидаемым из модельно-теоретических представлений; выявить возможные систематические погрешности и попытаться их устранить.

Теоретическое введение

§1. Внутренняя энергия идеального газа

В соответствии с моделью идеального газа изменение расстояния между молекулами при не ведет к изменению энергии взаимодействия. Поэтому внутренняя энергия идеального газа от объема не зависит. Так как потенциальная энергия взаимодействия U_потенц = const, то можно принять ее для идеального газа равной 0. Тогда U идеального газа представить, как сумму 3-х слагаемых:

U = U_п.х.д.м. + U_в.х.д.м. + U_{к.х.д.а.м.}, (1)

где:

U_п.х.д.м. – кинетическая энергия поступательного хаотического движения молекул,

U_в.х.д.м. – кинетическая энергия вращательного хаотического движения молекул,

U_{к.х.д.а.м.} – механическая энергия, связанная с колебательным хаотическим движением атомов в молекулах.

Внутренняя энергия данной массы идеального газа зависит только от температуры. Однако внутренняя энергия одной и той же массы различных газов при одной температуре может отличаться, что определяется числом степеней свободы молекул. Число степеней свободы i – количество независимых координат, задающих положение молекулы в пространстве.

По теореме Больцмана: в условиях термодинамического равновесия средняя энергия, приходящаяся на одну степень свободы п.х.д.м. и в.х.д.м. – кТ/2; на одну степень свободы к.х.д.а.м. – кТ.

Внутренняя энергия некоторой массы идеального газа:

(2)

где N – число молекул данного вида в системе.

Опыт показывает, (объяснение дает квантово-механическая теория), что в широком диапазоне температур молекулы двух- и трехатомных газов можно считать жесткими. Интервалы жесткости основных молекул, входящих в воздух: N₂ – (29¸3300) К; О₂ – (2,1¸3200) К; СО₂ – (300¸2000) К; HСl – (3,0¸3300) К. Обусловлено это свойство молекул тем, что между атомами, в них входящими, реализуется достаточно сильная химическая связь – ковалентная связь.

В этом приближении N молекул однокомпонентного газа обладают внутренней энергией:

(3)

где i – число степеней свободы, приходящихся на поступательное и вращательное хаотическое движение молекулы.

Таблица №1 (для жестких молекул).

Газ	Одноатомный	Двухатомный	Многоатомный
			Линейные молекулы	Пространственные молекулы
i	3	5	5	6

Для моля такого газа:

(4)

Для произвольной массы:

(5)

В ситуации многокомпонентного газа:

(6)

§2. Термическое и калорическое описание изопроцессов (V=const; p=const; T=const).

Если учесть уравнения и условия изопроцессов с идеальным газом и аналитическую зависимость внутренней энергии такого газа от Т, то первое начало термодинамики для произвольного элементарного процесса будет иметь вид:

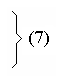
В соответствии с (1) характеристики изопроцессов можно представить в таблице 2.

Термическое и калорическое описание изопроцессов.

Таблица 2.

Процессы	А	Du	Q	Теплоемкость
				Сх	Схm
V=сonst (dV=0) P=cT	0		Qv=Du
P = const (dP = 0) V = сТ
T = const (dT = 0) PV = const		0	Qт = Ат	±¥	±¥