
- •§ 1. Основные формулы комбинаторики
- •Теорема о перемножении шансов
- •Урны и шарики
- •Выбор без возвращения, с учётом порядка
- •Выбор без возвращения и без учёта порядка
- •Выбор с возвращением и с учётом порядка
- •Выбор с возвращением и без учёта порядка
- •1.6. Формула полной вероятности и формула Байеса
- •Повторные независимые испытания
Теорема сложения для совместных событий
Суммой 2-х совместных событий называют событие, состоящее в появлении либо события A, либо события B, либо обоих сразу.
Теорема. Вероятность суммы 2-х совместных событий равна сумме вероятностей этих событий без учета их совместного появления. p(A+B)=p(A)+p(B)−p(AB)
Доказательство:
A+B=AB+AB+AB (сумма несовместных пар)
Тогда p(A+B)=p(AB)+p(AB)+p(AB)
Событие A=AB+AB,
Событие B=AB+AB
p(A+B)=p(A)−p(AB)+p(B)−p(AB)+p(AB)=p(A)+p(B)−p(AB)
Замечание: в этой теореме может существовать 2 различные ситуации.
p(A+B)=p(A)+p(B)−p(A)p(B), где A и B - независимые;
p(A+B)=p(A)+p(B)−p(A)p(B∖A), где A и B - зависимые;
Теоремы о вероятностях. Теоремы сложения несовместных событий.
Суммой 2-х несовместных событий A+B называется событие, состоящее в появлении либо события А, либо события B.
Теорема. Вероятность суммы 2-х несовместных событий равна сумме вероятностей этих событий p(A+B)=p(A)+p(B)
Доказательство.
Если n - общее число всех элементарных исходов;
m1 -- число исходов благоприятных событию A;
m2 -- число исходов благоприятных событию B;
p(A+B)=nm1+m2=nm1+nm2=p(A)+p(B)
Теорема. Вероятность суммы нескольких парно несовместных событий равна сумме вероятностей этих событий.
Доказательство проводится методом математической индукции.
Теорема. Сумма вероятностей событий, образующих полную группу равна 1.
p(A1)+...+p(Ak)=1
Доказательство. Согласно теореме p(A1+A2+...Ak)=p(A1)+p(A2)+...p(Ak).
Так как события Ai образуют полную группу, то сумма событий A1+A2+...Ak есть достоверное событие (хотя бы одно произойдет).
Следовательно, p(A1+A2+...Ak)=1, а потому p(A1)+...+p(Ak)=1.
ЧТД
Теорема. Сумма вероятностей противоположных событий равна 1. p(A)+p(A)=1
Доказательство производится на основании предыдущей теоремы, так как эти события образуют полную группу, несовместны.
Множества и операции над множествами
Напомним основные обозначения, понятия, относящиеся к множествам, которых будем придерживаться дальше.
Начнем с основного понятия, которое встречается практически в каждом разделе математики - это понятие множества.
Множество - это совокупность, набор элементов, объединенных общими свойствами.
Множества
обозначаются заглавными латинскими
буквами 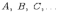 ,
а элементы множества строчными латинскими
буквами
,
а элементы множества строчными латинскими
буквами 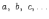 .
.
Запись 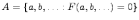 означает,
что есть множество
означает,
что есть множество 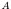 с
элементами
с
элементами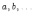 ,
которые связаны между собой какой-то
функцией
,
которые связаны между собой какой-то
функцией 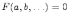 .
.
Замечание. Элементы в множество входят по одному разу, т.е. без повторений.
Основные операции:
Принадлежность элемента множеству:
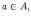
где  --
элемент и
--
множество (элемент
принадлежит
множеству
).
--
элемент и
--
множество (элемент
принадлежит
множеству
).
Непринадлежность элемента множеству:
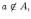
где -- элемент и -- множество (элемент не принадлежит множеству ).
Объединение множеств:
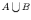 .
.
Объединением
двух множеств
и 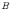 называется
множество
называется
множество 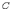 ,
которое состоит из элементов
множеств
и
,
т.е.
,
которое состоит из элементов
множеств
и
,
т.е.
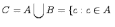 или
или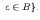
Пересечение множеств:
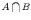 .
.
Пересечением двух множеств и называется множество , которое состоит из общих элементов множеств и , т.е.
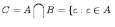 и
и
Разность множеств:
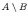 .
.
Разностью двух множеств и , например, множество минус множество , называется множество , которое состоит из элементов множества , которых нет в множестве , т.е.
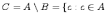 и
и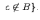
Симметрическая разность множеств:
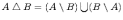 .
.
Симметрической разностью двух множеств и называется множество , которое состоит из не общих элементов множеств и , т.е.
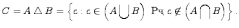
Дополнение множества:
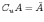 .
.
Если
предположим, что множество
является
подмножеством некоторого универсального
множества 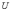 ,
тогда определяется операция дополнения:
,
тогда определяется операция дополнения:
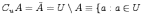 и
и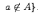
Вхождение одного множества в другое множество:
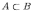 .
.
Если любой элемент множества является элементом множества , то говорят, что множество есть подмножество множества (множество входит в множество ).
Не вхождение одного множества в другое множество:
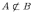 .
.
Если
существует элемент множества 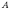 ,
который не является элементом множества
,
который не является элементом множества 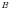 ,
то говорят, что множество
не
подмножество множества
(множество
не
входит в множество
).
,
то говорят, что множество
не
подмножество множества
(множество
не
входит в множество
).
§ 1. Основные формулы комбинаторики
В данном разделе мы займёмся подсчётом числа «шансов». О числе шансов говорят, когда возможно несколько результатов какого-либо действия (извлечение карты из колоды, подбрасывание кубика или монетки). Число шансов — это число способов проделать это действие или, что то же самое, число возможных результатов этого действия.
Теорема о перемножении шансов
Пусть одно действие можно проделать пятью способами, а другое — двумя. Каким числом способов можно проделать пару этих действий?
Теорема
1. Пусть
множество  состоит
из
состоит
из  элементов:
элементов: 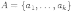 ,
а множество
,
а множество 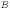 —
из
—
из 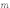 элементов:
элементов: 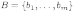 .
Тогда можно образовать ровно
.
Тогда можно образовать ровно 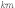 пар
пар 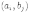 ,
взяв первый элемент из множества
,
а второй — из множества
.
,
взяв первый элемент из множества
,
а второй — из множества
.
Замечание 1. Можно сформулировать утверждение теоремы 1 так: если первый элемент можно выбрать способами, а второй элемент — способами, то пару элементов можно выбрать способами.
Доказательство. С
элементом 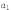 мы
можем образовать
пар:
мы
можем образовать
пар: 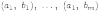 .
Столько же пар можно составить с
элементом
.
Столько же пар можно составить с
элементом 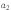 ,
столько же — с элементом
,
столько же — с элементом 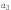 и с любым
другим из
элементов
множества
.
Т.е. всего возможно
пар,
в которых первый элемент выбран
из множества
,
а второй — из множества
.
и с любым
другим из
элементов
множества
.
Т.е. всего возможно
пар,
в которых первый элемент выбран
из множества
,
а второй — из множества
.
QED
Упражнение 1. С помощью теоремы 1 доказать, что:
а)
при подбрасывании трёх монет возможно 2·2·2=8 различных результатов;
б)
бросая дважды игральную кость, получим 6·6=36 различных результатов;
в)
трёхзначных чисел бывает 9·10·10=900;
г)
трёхзначных чисел, все цифры которых различны, существует 9·9·8;
д)
чётных трёхзначных чисел возможно 9·10·5.
Урны и шарики
Есть
урна (ящик), содержащая  пронумерованных
объектов (шаров). Мы выбираем из этой
урны
шаров;
результатом выбора является набор
из
шаров.
Нас интересует, сколькими способами
можно выбрать
шаров
из
,
или сколько различных результатов может
получиться. На этот вопрос нельзя дать
однозначный ответ, пока мы не определимся:
а) с тем, как организован выбор (можно
ли шары возвращать в урну), и б) с тем,
что понимается под различными результатами
выбора.
пронумерованных
объектов (шаров). Мы выбираем из этой
урны
шаров;
результатом выбора является набор
из
шаров.
Нас интересует, сколькими способами
можно выбрать
шаров
из
,
или сколько различных результатов может
получиться. На этот вопрос нельзя дать
однозначный ответ, пока мы не определимся:
а) с тем, как организован выбор (можно
ли шары возвращать в урну), и б) с тем,
что понимается под различными результатами
выбора.
Рассмотрим следующие возможные способы выбора.
1.
Выбор с возвращением: каждый вынутый шар возвращается в урну, каждый следующий шар выбирается из полной урны. В полученном наборе из номеров шаров могут встречаться одни и те же номера.
2.
Выбор без возвращения: вынутые шары в урну не возвращаются, и в полученном наборе не могут встречаться одни и те же номера.
Условимся, какие результаты выбора (наборы из номеров шаров) мы будем считать различными. Есть ровно две возможности.
1.
Выбор с учётом порядка: два набора номеров шаров считаются различными, если они отличаются составом или порядком номеров. Так, при выборе трёх шаров из урны, содержащей 5 шаров, наборы (1, 5, 2), (2, 5, 1) и (4, 4, 5) различны, если порядок учитывается.
2.
Выбор без учёта порядка: два набора номеров шаров считаются различными, если они отличаются составом. Наборы, отличающиеся лишь порядком следования номеров, считаются одинаковыми.
Так, наборы (1, 5, 2) и (2, 5, 1) не различаются и образуют один и тот же результат выбора, если порядок не учитывается.
Подсчитаем, сколько возможно различных результатов для каждой из четырёх схем выбора (выбор с возвращением или без, и в каждом из этих случаев — с учётом порядка или без).
Упражнение 2. Перечислить все возможные результаты в каждой из четырёх схем при выборе двух шаров из четырёх. Например, при выборе с возвращением и без учёта порядка: (1, 1), (1, 2), (1, 3), (1, 4), (2, 2), (2, 3), (2, 4), (3, 3), (3, 4), (4, 4).
