3. Статистическое описание результатов наблюдений для св X
Найдем
значения
и
из 100 чисел, длину разрядов
и границы интервалов
Результаты занесем в таблицу 1.
Таблица 1
Объем выборки |
n = |
100 |
Количество разрядов |
k = |
10 |
Длина разрядов |
h = |
5,4 |
Минимум |
xmin = |
51 |
Максимум |
xmax = |
105 |
Составляем интервальный ряд распределения для СВ Х.
Найдем
числа
значений СВ, попавших в каждый разряд
и частоту
попаданий значений СВ в каждый разряд
Плотность
(х)
частоты попаданий значений СВ в каждый
разряд рассчитаем по формуле
.
Полученные данные занесем в таблицу 2.
Для
определения статистической
плотности вероятности
вычисляем значения
.
Зависимость между h
и
оформим в виде графика: над каждым
интервалом
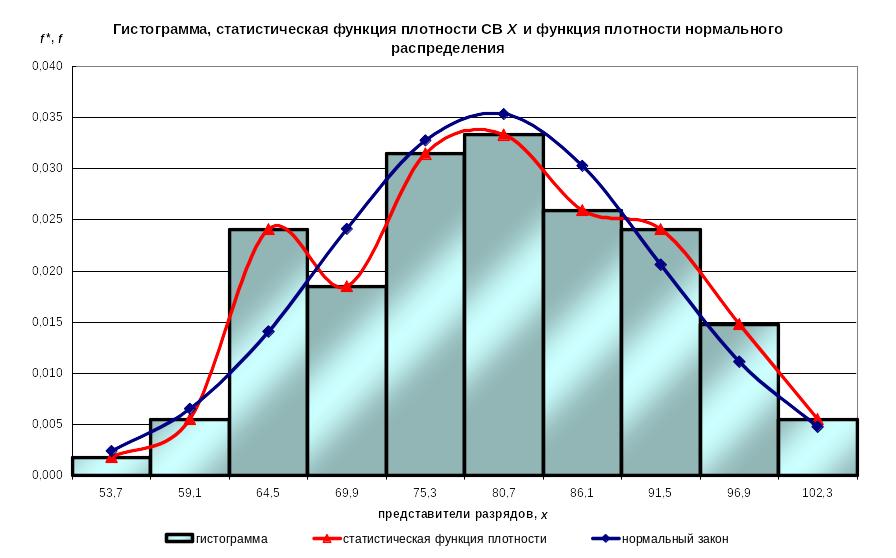
строим прямоугольник, высота которого
равна
.
Такой график называют гистограммой
(см. рисунок 1).
Так как есть разряды, содержащие менее 5 значений, произведем объединение первых трех и последних двух разрядов. Соответствующие значения нанесем на рисунок 1 пунктирными линиями.
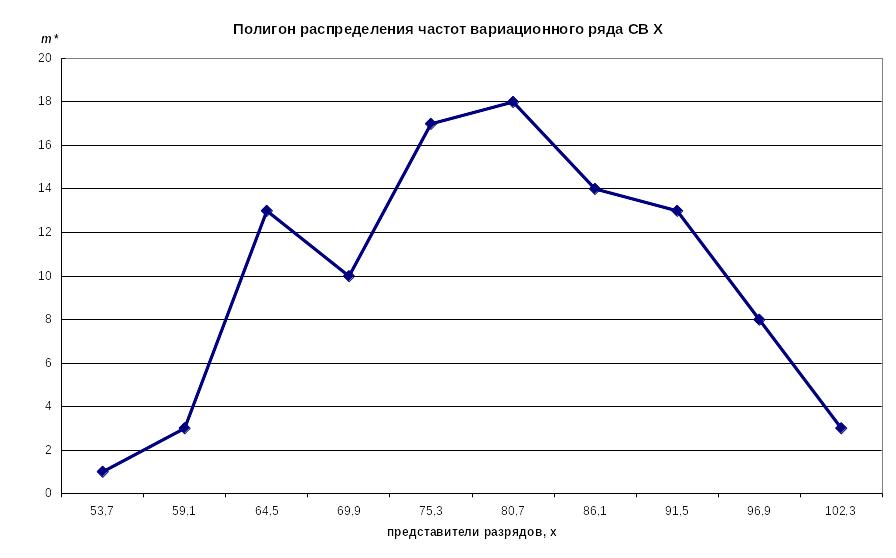
На рисунке 2 приведен полигон частот.
Для
построения статистической функции
распределения F*(x)
(см. рисунок 3) все значения СВ, попавшие
в i-ый
разряд, заменяем одним, совпадающим с
серединой разряда
и считаем, что это значение повторяется
раз.
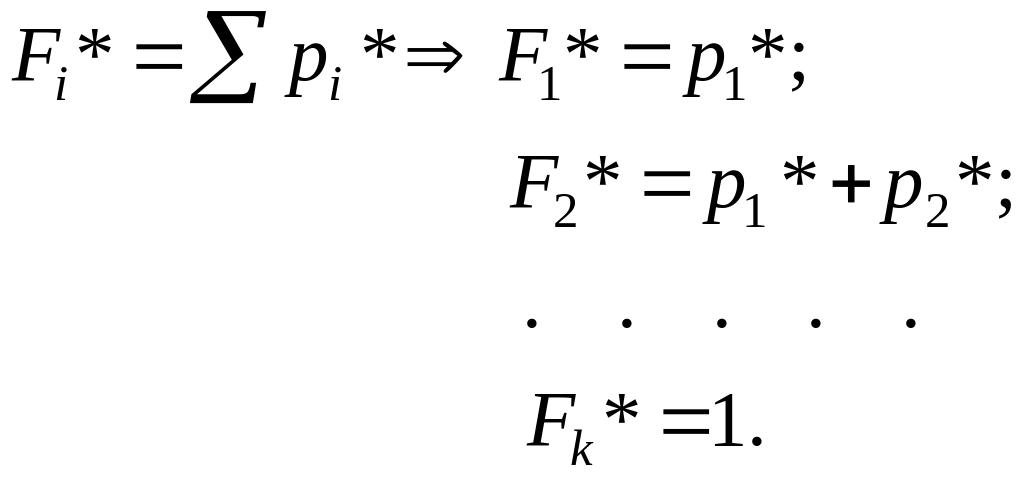
Таблица 2
Границы разрядов |
51 |
56,4 |
61,8 |
67,2 |
72,6 |
78 |
83,4 |
88,8 |
94,2 |
99,6 |
105 |
|
Представитель
разряда
|
53,7 |
59,1 |
64,5 |
69,9 |
75,3 |
80,7 |
86,1 |
91,5 |
96,9 |
102,3 |
|
|
Частота mi* |
1 |
3 |
13 |
10 |
17 |
18 |
14 |
13 |
8 |
3 |
|
100 |
mi* |
53,7 |
177,3 |
838,5 |
699 |
1280,1 |
1452,6 |
1205,4 |
1189,5 |
775,2 |
204,6 |
|
7875,9 |
( )2mi* |
2883,69 |
10478,43 |
54083,25 |
48860,1 |
96391,53 |
117224,8 |
103784,94 |
108839,3 |
75116,88 |
20930,58 |
|
638593,5 |
Накопленные относительные частоты Fi*(х) |
0,01 |
0,04 |
0,17 |
0,27 |
0,44 |
0,63 |
0,77 |
0,9 |
0,98 |
1 |
|
|
Плотности fi*(х) |
0,002 |
0,006 |
0,024 |
0,019 |
0,031 |
0,033 |
0,026 |
0,024 |
0,015 |
0,006 |
|
|
Таблица 4
Границы разрядов |
32 |
34,4 |
36,8 |
39,2 |
41,6 |
44 |
46,4 |
48,8 |
51,2 |
53,6 |
Итого |
Представитель разряда |
33,2 |
35,6 |
38 |
40,4 |
42,8 |
45,2 |
47,6 |
50 |
52,4 |
54,8 |
|
Частота mi* |
1 |
2 |
10 |
8 |
21,5 |
19,5 |
15 |
12 |
8 |
3 |
100 |
|
33,2 |
71,2 |
380 |
323,2 |
920,2 |
881,4 |
714 |
600 |
419,2 |
164,4 |
4506,8 |
( )2mi* |
1102,24 |
2534,72 |
14440 |
13057,38 |
39384,56 |
39839,28 |
33986,4 |
30000 |
21966,08 |
9009,12 |
205319,7 |
Накопленные относительные частоты Fi*(у) |
0,01 |
0,03 |
0,13 |
0,21 |
0,425 |
0,62 |
0,77 |
0,89 |
0,97 |
1 |
|
Плотности fi*(у) |
0,0042 |
0,0083 |
0,0417 |
0,0333 |
0,0896 |
0,0813 |
0,0625 |
0,05 |
0,0333 |
0,0125 |
|
mi*
Р и с у н о к 1
Р и с у н о к 2
Р и с у н о к 3
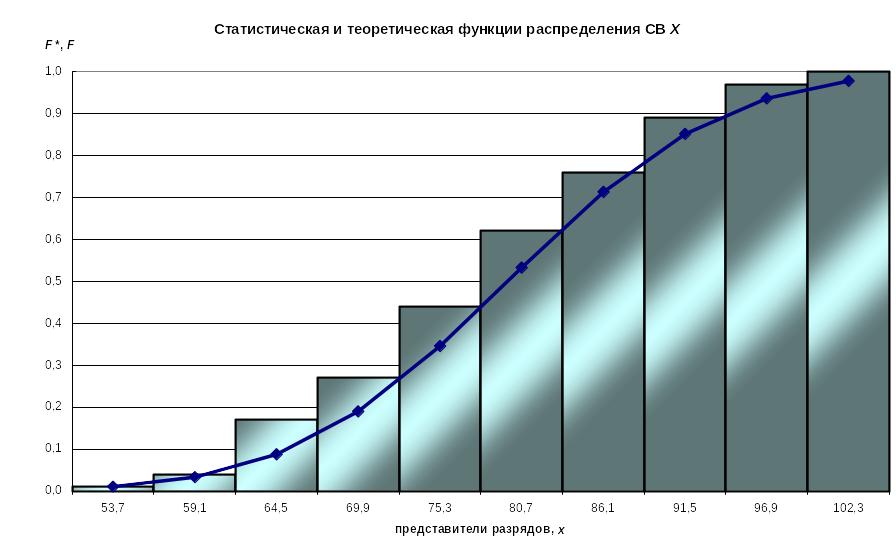
Построим статистическую функцию распределения по значениям предпоследней строки таблицы 2 (см. рисунок 3).