
Математическое моделирование (Барцев) вопросы к экзамену
.pdf
Циклы, которые видны на рис. 2.1, наблюдаются в природе (рис. 2.2). Их можно описать следующим образом: когда количество хищников возрастает, они истребляют жертв и количество

жертв убывает. Когда жертв становится слишком мало, их начинает не хватать для пропитания хищников и количество хищников начинает убывать. Когда хищников становится достаточно мало, они начинают поедать меньшее количество жертв и количество жертв начинает возрастать. Количество пищи для хищников увеличивается, и хищники размножаются. Цикл замыкается, и все начинается сначала. Таким образом, система "хищник–жертва" стабильна: не происходит ни неограниченного роста количества животных, ни полного вымирания.
12.Порядок химических реакций, размерности констант скоростей реакции.
•В зависимости от вида кинетического уравнения, связывающего скорость реакции
с концентрацией реагирующих веществ, различают реакции нулевого,
первого, второго и третьего порядка.
•Если скорость реакции не зависит от концентрации реагирующих веществ, то реакция имеет нулевой порядок. Если скорость реакции зависит от концентрации вещества в первой степени, то это реакция первого порядка; если во второй степени, то это реакция второго порядка и т.д.
•Показатель степени концентрации реагирующего вещества (а, р, 5) в
кинетическом уравнении реакции называется порядком реакции по данному веществу (А, В и D соответственно).
•Общим порядком химической реакции, или просто порядком реакции, называется величина, равная сумме показателей степени концентраций реагентов в кинетическом уравнении реакции. Общий порядок реакции = а + β + σ + ....
•Для реакций нулевого порядка кинетическое уравнение имеет следующий вид:
•Скорость реакции нулевого порядка постоянна во времени и не зависит от концентраций реагирующих веществ. Это характерно для тех процессов, скорость которых меньше скорости доставки реагирующих веществ к месту поведения реакции. Часто это имеет место в гетерогенных реакциях, идущих на поверхности раздела фаз.
•По нулевому порядку идут и реакции, скорость которых лимитируется подачей
энергии, необходимой для активации реагирующих молекул (например,

фотохимические реакции, где определяющим фактором служит, например, количество поглощенного света, а не концентрация вещества). Кроме того, часто в каталитических реакциях скорость определяется концентрацией катализатора и не зависит от концентрации реагирующих веществ.
13.Формула Михаэлиса-Ментен. Условие ее применимости.

Благодаря высокому сродству связывания и образованию ES-комплекса резко возрастает число молекул субстрата, вступающих в реакции.
[Et] – общая концентрация фермента

Определение величины Кm имеет важное значение при выяснении механизма действия эффекторов на активность ферментов и т.д. Константу Михаэлиса можно вычислить по классическому графику Михаэлиса-Ментен. Отрезок на абсциссе, соответствующий скорости, равной половине максимальной, будет представлять собой Кm.
Высокое сродство фермента к субстрату характеризуется низкой величиной Кm и наоборот.

14.Вывод формулы стационарной скорости ферментативной реакции методом графов.
Пользоваться графиком, построенным в прямых координатах зависимости начальной скорости реакции v0 от начальной концентрации субстрата [S0], неудобно, поскольку максимальная скорость Vmax является в данном случае асимптотической величиной и определяется недостаточно точно. Для более удобного графического представления экспериментальных данных Г. Лайнуивер и Д. Бэрк преобразовали уравнение по методу двойных обратных величин исходя из того принципа, что если существует равенство между двумя какими-либо величинами, то и обратные величины также будут равны. которое получило название уравнения Лайнуивера–Бэрка (см. слайд). Это уравнение прямой линии: у = ах + b. Если теперь в соответствии с этим уравнением построить график в координатах 1/v (y) от l/[S] (x), то получим прямую линию, тангенс угла наклона который будет равен величине Km/Vmax; отрезок, отсекаемый прямой от оси ординат, представляет собой l/Vmax (обратная величина максимальной скорости). Если продолжить прямую линию за ось ординат, тогда на абсциссе отсекается отрезок, соответствующий обратной
величине константы Михаэлиса – 1/Кm. Таким образом, величину Кm можно вычислить из данных наклона прямой и длины отрезка, отсекаемого от оси ординат, или из длины отрезка, отсекаемого от оси абсцисс в области отрицательных значений.

15.Алгебра высказываний. Область применимости. Сложные высказывания. Логические операции (связки) и вентильные схемы.
Алгебра высказываний была разработана для того, чтобы можно было определять истинность или ложность составных высказываний, не вникая в их содержание.
В алгебре высказываний суждениям (простым высказываниям) ставятся в соответствие логические переменные, обозначаемые прописными буквами латинского алфавита.
Рассмотрим два простых высказывания:
А = «Два умножить на два равно четырем». В = «Два умножить на два равно пяти».
Высказывания, как уже говорилось ранее, могут быть истинными или ложными. Истинному высказыванию соответствует значение логической переменной 1, а ложному
— значение 0. В нашем случае первое высказывание истинно (А = 1), а второе ложно (В =
0).
В алгебре высказываний высказывания обозначаются именами логических переменных, могут принимать лишь два значения:
«истина» (1) и «ложь» (0).
До сих пор мы рассматривали простые высказывания. На основании простых высказываний могут быть построены составные высказывания. Например, высказывание «Процессор является устройством обработки информации и принтер является устройством печати» является составным высказыванием, состоящим из двух простых, соединенных союзом «и».
Если истинность или ложность простых высказываний устанавливается в результате соглашения на основании здравого смысла, то истинность или ложность составных высказываний вычисляется с помощью использования алгебры высказываний.
Приведенное выше составное высказывание истинно, так как истинны входящие в него простые высказывания.
В алгебре высказываний над высказываниями можно производить определенные логические операции, в результате которых получаются новые, составные высказывания.
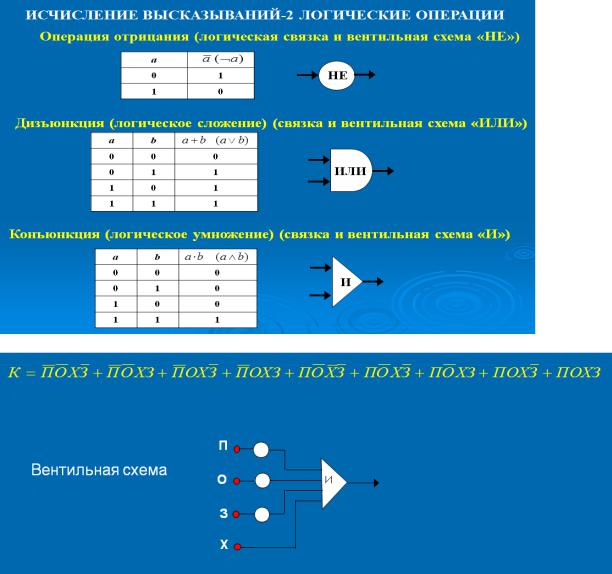
Для образования новых высказываний наиболее часто используются базовые логические операции, выражаемые с помощью логических связок «и», «или», «не».
16.Таблицы истинности формул алгебры высказываний.

Тип задач.
1.Применение метода отражения от биссектрисы к анализу дискретной модели.
2.Нарисовать графики производной и интеграла по графику функции.
3.Погасить вспышки численности в программной модели Лотки-Вольтерра.
4.Вывести формулу стационарной скорости ферментативной реакции методом графов.
5.Проверить эквивалентность формул алгебры высказываний методом таблицы истинности.
6.Нахождение отображения для Числовой Машины.
