Математическое моделирование (Барцев) вопросы к экзамену

6.Логика развития дискретной модели популяции, усложнение динамических режимов, рост адекватности. Использовать фазовый портрет и метод отражения от биссектрисы.

См. документ

7.Понятие производной, графический смысл производной. Свойства производной (производная суммы, произведения, частного функций. Нахождение производных сложных функций). Выявление точек подозрительных на экстремум, определение типа экстремума (минимум, максимум) или его отсутствия (перегиб).

Производная - это предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если таковой предел существует.

Геометрический смысл производной. Производная в точкеравнаx угловому коэффициенту касател

0

графику функцииy = f(x) в этой точке.

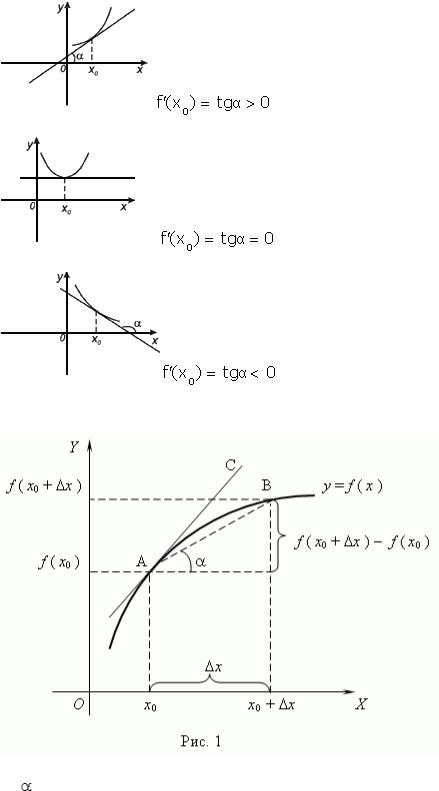
Рассмотримрафикг функцииy = f ( x ):

Из рис.1 видно, что для любыхA иBдвухграфикаточекфункции:f(x0+Δx)−f(x0)Δx где - угол наклона секущейAB.

Таким образом, разностное отношение равно угловому коэффициенту секущей. Если зафиксироватьA иточкудвигать по направлениюB,к тонейxΔxточкунеограниченно уменьшается приближается к 0, а АВсекущаяприближается к касательнойАС.

Следовательно, предел разностного отношения равен угловому коэффициентуA. каса Отсюда следует:

производная функции в точке есть угловой коэффициент касательнойив этойк графикуточке. э

В этом и состоит геометрический смысл производной.

См тетр.

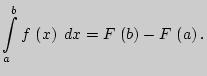
8.Понятие первообразной и интеграла. Свойства интеграла. Неопределенный и определенный интегралы. Формула Ньютона-Лейбница.

Определение: 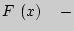первообразная функции 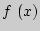, если

.Правила нахождения первообразных:

1. Постоянный коэффициент можно выносить за знак интегрирования:

функции соответствует первообразная .

2. Первообразная суммы функций равна сумме первообразных этих функций:

сумме функций 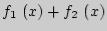соответствует сумма первообразных .

Формула Ньютона - Лейбница (для нахождения значения определенного интеграла):

Геометрический смысл определенного интеграла :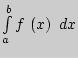

Абсолютная величина значения определенного интеграла равна площади криволинейной трапеции, ограниченной графиком подынтегральной

функции , осью абсцисс и прямыми .

Основное свойство первообразной

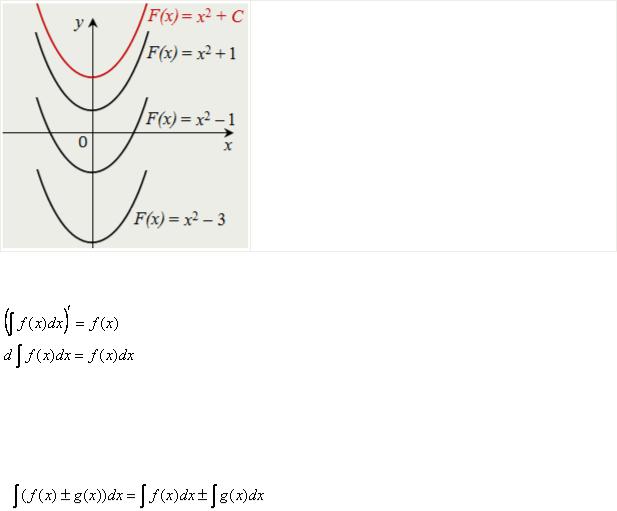
1 Если F(x) — первообразная для функции f(x) на заданном промежутке, то функция f(x) имеет бесконечно много первообразных, и все эти первообразные можно записать в виде F(x) + С, где С — произвольная постоянная.

► Например.

Функция F(x) = х2 + 1 является первообразной для функции f(x) = 2х, так как F'(x) = (х2 + 1)' = 2x = f(x);

функция F(x) = х2 – 1 является первообразной для функции f(x) = 2х , так как F'(x) = (х2 – 1)' = 2x = f(x);

функция F(x) = х2 – 3 является первообразной для функции f(x) = 2х , так как F'(x) = (х2 –3)' = 2x = f(x);

любая функция F(x) = х2 + С, где С — произвольная постоянная, и только такая функция, является первообразной для

функции f(x) = 2х. ◄

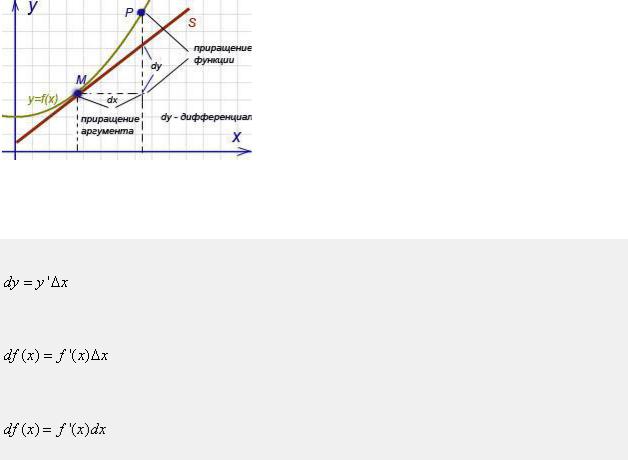
2 Производная от неопределённого интеграла равна подынтегральной функции; дифференциал от неопределённого интеграла равен подынтегральному выражению:

3 Константу можно вынести из-под знака интеграла

То есть, если 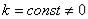, то

4) Неопределённый интеграл от алгебраической суммы функций равен алгебраической сумме интегралов:

Определенный интеграл от функции f(x) в пределах от a до b

вводится как предел суммы бесконечно большого числа слагаемых, каждое из которых стремится к нулю:

9.Дифференциал. Связь производной и дифференциала. Свойства дифференциала. Простейшее дифференциальное уравнение экспоненциального роста (отмирания). Применимость к описанию динамики популяции.

Определение. Дифференциалом функции в некоторой точке x называется главная, линейная часть приращения функции.

Дифференциал функции y = f(x) равен произведению её производной на приращение независимой переменной x (аргумента).

Это записывается так:

или

или же

Геометрический смысл дифференциала. Дифференциал функции y = f(x) равен приращению ординаты касательной S, проведённой к графику этой функции в точке M(x; y), при

изменении x (аргумента) на величину (см. рисунок).

См. тетр.

10.Уравнение Ферхюльста. Смыл входящих в него переменных и параметров. Логистическая функция, как решение уравнения Ферхюльста. Области применения логистической функции.

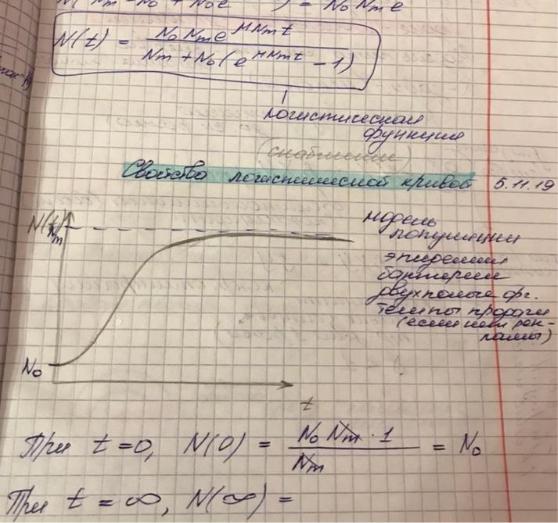
Частым явлением в природе является ограниченность ресурсов (пищевых, территориальных) и, как следствие, внутривидовая конкуренция. Как правило, если численность популяции очень мала, то конкуренция не влияет на удельную скорость роста популяции r. Когда же численность возрастает и приближается к некоторому предельному значению K, удельная скорость роста падает до нуля. Предельное значение K называется емкостью экологической ниши популяции. Величина К соответствует такой численности популяции, при которой фактическая скорость воспроизводства в результате конкуренции настолько снижена, что популяция в целом может только восстанавливать в каждом поколении свою численность. В этот момент количество родившихся особей уравновешивается количеством погибших.

Если начальная численность популяции меньше величины экологической емкости популяции, то с течением времени ее размер будет расти, приближаясь к своему предельному значению K. При этом, если начальная численность составляет менее

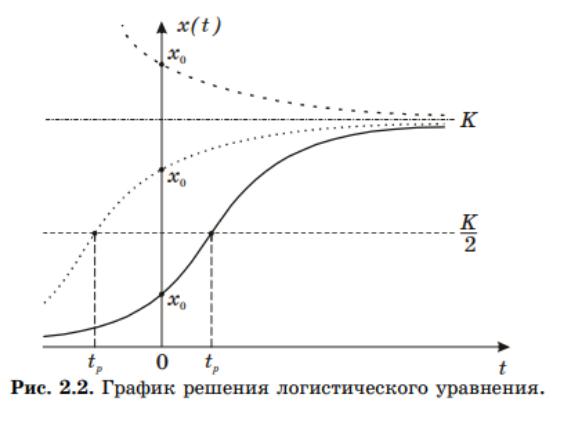
половины емкости экологической ниши, на начальном этапе скорость роста популяции будет возрастать, пока численность не достигнет значения 2 K , а затем начнет снижаться, стремясь к нулю. Если начальная численность популяции составляет более половины емкости экологической ниши, то размер популяции будет увеличиваться, стремясь к значению K, а скорость ее роста будет неуклонно снижаться. Изменение характера развития популяции (переход от возрастания скорости роста к снижению в точке ( ) 2 K x t = ) произошло до того, как исследователь начал за ней наблюдать (т.е. до момента времени t = 0 ). Если же размер популяции в начальный момент времени больше предельно возможного значения, то численность популяции будет снижаться (рис. 2.2).

11.Модель Лотки-Вольтерра. Смысл переменных и коэффициентов. Фазовый портрет системы. Различие свойств уравнений на численность и на биомассу.

Вкачестве примера естественного регулирования процесса внутривидовой конкуренции можно привести правило Лотки–Вольтерры, которое отражает взаимоотношения в пищевой цепи консументов и продуцентов, или хищника и жертвы.

Рост численности и плотности популяций не бесконечен. Рано или поздно возникает угроза недостатка ресурсов среды (корм, убежища, места для размножения, истощение почвы, чрезмерное затенение). У каждой популяции свои пределы ресурсов, называемые емкостью среды. По мере ее снижения усиливается внутривидовая конкуренция. Включаются разные механизмы регуляции численности. У растений начинается самоизреживание и дифференциация растений по размерам и физиологическому состоянию, у животных падает рождаемость, усиливается агрессия, они начинают расселяться на свободные территории, внутри популяций начинаются эпидемии. Реакция у каждого вида на собственное перенаселение разная, но результат для всех один – торможение развития и размножения.

На рис. 5 изображена графическая модель Лотки–Вольтерры. Она позволяет показать основную тенденцию в отношениях "хищник-жертва", которая заключается в том, что колебания численности популяций хищника согласуются с колебаниями численности популяции жертвы. При этом циклы нарастания и спада численности хищников и жертвы по отношению друг к другу 11 смещены. Когда велика численность жертв (пищевой ресурс), увеличивается численность хищников, но не беспредельно, а до тех пор, пока не возникнет напряжение с пищей. Снижение

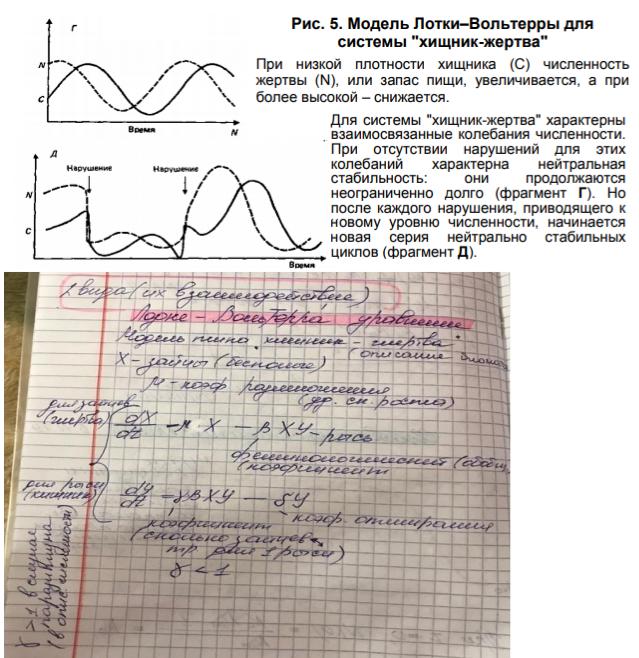
запасов пищи приводит к усилению внутривидовой конкуренции и снижению численности хищника, а это, в свою очередь, вновь приводит к увеличению численности жертвы.