Глава 20. Функции сосудистой системы 499

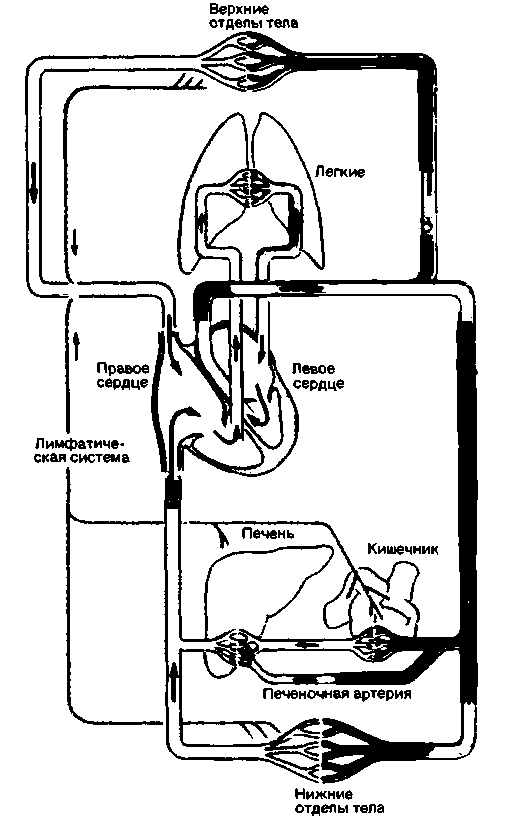
Рис. 20.1. Схема сердечно-сосудистой системы. Сосуды, содержащие насыщенную кислородом кровь, закрашены красным, а сосуды, содержащие частично дезоксигенироеанную кровь,-розовым. Малый и большой круги кровообращения образуют замкнутую цепь. Лимфатическая система (показана серым) осуществляет дополнительную дренажную функцию

крови, то они предъявляют к правому сердцу относительно постоянные требования и выполняют в основном функции газообмена и теплоотдачи. Поэтому для регуляции легочного кровотока требуется менее сложная система.

Кроме системы кровеносных сосудов существует система лимфатических сосудов, собирающих жидкость и белки из межклеточного пространства и переносящих эти вещества в кровеносную систему (рис. 20.1).

20.1. Основы гемодинамики

Движущей силой кровотока служит разность давлений между различными отделами сосудистого русла: кровь течет от области высокого давления к области низкого давления. Этот градиент давления служит источником силы, преодолевающей гидродинамическое сопротивление; последнее широко варьирует как во времени, так и в разных отделах сосудистого русла и зависит от архитектуры этого русла (например, числа, длины, диаметра и степени ветвления сосудов той или иной области) и вязкости крови [2, 4, 5, 15, 19, 20, 33].

Физические основы гемодинамики

Скорость кровотока, давление и сопротивление.

Все факторы, влияющие на кровоток, в конечном счете могут быть приближенно сведены к уравнению, сходному с законом Ома:

О)

Из этого уравнения следует, что объемная скорость кровотока в каком-либо отделе кровеносного русла равна отношению разности среднего давления Ρ в артериальной и венозной частях этого отдела (или в любых других частях) к гидродинамическому сопротивлению R этого отдела.

Объемная скорость кровотока отражает кровоснабжение того или иного органа. Она равна объему крови, протекающему через поперечное сечение сосудов, и измеряется в единицах мл/с. Ее можно вычислить, исходя из линейной скорости кровотока ( ) через поперечное сечение сосуда и площади этого сечения ( ):

(2)

В соответствии с законом неразрывности струи

объемная скорость тока жидкости в системе из трубок разного диаметра (т. е. в системе, подобной кровеносной) постоянна независимо от поперечного сечения трубки. Следовательно, для двух последовательных сегментов (а и б) (рис. 20.2) справедливо равенство

(3)

Таким образом, если через последовательно соединенные трубки протекает жидкость с постоянной объемной скоростью, линейная скорость движения жидкости в каждой трубке обратно пропорциональна площади ее поперечного сечения.

Давление в кровеносной системе (артериальное и венозное) равно отношению силы, с которой кровь действует на стенки сосудов, к площади этих стенок. Поскольку в клинике кровяное давление издавна измеряется при помощи ртутных манометров, его

500 ЧАСТЬ V. КРОВЬ И СИСТЕМА КРОВООБРАЩЕНИЯ

Рис. 20.2. Изменения линейной скорости кровотока и объемная скорость кровотока в последовательно соединенных трубках разного сечения

обычно выражают в миллиметрах ртутного столба, хотя иногда значения приводят в сантиметрах водного столба (1 мм рт. ст « 13,6 мм вод. ст. « « 133 Па; 10 мм вод. ст. « 98 Па). (Пересчет на другие единицы приведен на с. 845.)

Гидродинамическое сопротивление R нельзя измерить непосредственно, однако его можно вычислить из уравнения (1), зная разность давлений между двумя отделами сосудистой системы и объемную скорость.

Гидродинамическое сопротивление обусловлено внутренним трением между слоями жидкости и между жидкостью и стенками сосуда. Оно зависит от размеров сосуда, а также от вязкости и типа течения жидкости.

Гидродинамическое сопротивление в системе трубок. Если трубки соединены последовательно, то их общее сопротивление в соответствии с первым законом Кирхгофа равно сумме сопротивления всех трубок:

R₀ = R₁ + R₂ + .... (4)

Если же трубки соединены параллельно (как, например, сосудистые сети различных органов), то, согласно второму закону Кирхгофа, складываются их проводимости:

С₀ = С₁+С₂ + .... (5)

Поскольку проводимость-это величина, обратная сопротивлению, то

(6) или в соответствии с уравнением (1)

(7)

т.е. при постоянном градиенте давления объемная скорость возрастает пропорционально проводимости.

Учитывая, что проводимость есть величина, обратная сопротивлению, общее сопротивление системы из двух параллельных трубок равно

(8)

Таким образом, общее сопротивление нескольких параллельных трубок одинакового диаметра равно сопротивлению одной трубки, деленному на число трубок; таким образом, это общее сопротивление значительно меньше, чем у каждой отдельной трубки.

Вязкость крови. Если текущая жидкость соприкасается с неподвижной поверхностью (например, при движении жидкости в трубке), то слои такой жидкости перемещаются с различными скоростями. В результате между этими слоями возникает напряжение сдвига: более быстрый слой стремится вытянуться в продольном направлении, а более медленный задерживает его. Показателем, отражающим это «внутреннее сопротивление» жидкости, служит ее вязкость η.

Для многих жидкостей вязкость η-это постоянная величина, зависящая от температуры. Согласно уравнению Ньютона, эта величина равна отношению напряжения сдвига τ (силы, приходящейся на единицу площади) к градиенту скорости между соседними слоями γ (скорости сдвига):

(9)

Из уравнения Хагена-Пуазейля (см. ниже) следует, что на силы, сдвигающие слои жидкости относительно друг друга (т.е. приводящие жидкость в движение и поддерживающие это движение), влияет не только давление, но также радиус и длина сосуда.

Вязкость часто выражают в относительных единицах, принимая вязкость воды при 20 °С (10³Па·с) за 1,0.

Вязкость гомогенных (ньютоновских) жидкостей (например, воды, раствора электролитов, плазмы крови) постоянна. Кровь состоит из плазмы и форменных элементов и поэтому является гетерогенной (неньютоновской) жидкостью; вязкость ее варьирует в зависимости в основном от количества клеток и в меньшей степени от содержания белков в плазме. Кроме того, вязкость гетерогенных жидкостей зависит также от размеров (радиуса и длины) трубок, по которым они текут.

У человека вязкость крови составляет 3-5, а плазмы-1,9-2,3 относительных единиц (рис. 20.3).

Вязкость крови в сосудах. Приведенные выше значения относительной вязкости справедливы лишь для сравнительно быстрого тока крови (т.е. высокого напряжения свита) и нормального состава крови (гематокрит около 40 и содержание белков в плазме 6,5-8,0 г/дл). При низкой скорости кровотока (а следовательно, и при малом напряжении