Венгерский метод.

Используется при решении задач о назначениях. Задача о назначениях заключается в выборе такого распределения ресурсов по объектам, при которых минимизируется стоимость назначений. Предполагается, что каждый ресурс назначается ровно один раз и каждому объекту приписывается ровно один ресурс.

Ресурсы	Объекты	Критерий эффективности
Рабочие	Рабочие места	Время
Грузовые автомобили	Маршруты	Затраты
Станки	Участки	Объем переработанной продукции
Экипажи	Рейсы	Время простоя
Коммивояжер	Города	Товарооборот

Постановка задачи: пусть необходимо выполнить n работ . Для этого используются n исполнителей , каждый из которых в состоянии выполнять любую работу. Известны затраты на выполнение j-ым исполнителем i-ой работы. Требуется назначить каждого исполнителя на одну работу так, чтобы минимизировать суммарные затраты. Введем переменную величину , отражающее фактическое назначение.

, если на i-ю работу назначает j-й исполнитель, – иначе.

при следующих ограничениях:

1. на каждую работу должен быть назначен только один исполнитель

2. каждый исполнитель должен быть назначен только на одну работу

Задача назначения относится к транспортной, если

Если задача о назначениях открытая, то необходимо добавить либо дополнительный ресурс, либо дополнительный объект.

Если задача о назначении ставится при условиях получения максимальной эффективности, то ее необходимо свести к задаче на минимум. Для этого отыскивают

максимальный элемент в каждом из столбцов матрицы и вычитают каждый элемент матрицы из максимального элемента соответствующего столбца.

Алгоритм:

I. Подготовительный этап.

Если задача на максимум, то перевести в задачу на минимум.

В каждой строке находим минимальный элемент, который вычитаем из всех элементов соответствующей строки матрицы. В результате преобразования в каждой строке матрицы появляется хотя бы один нуль. Заканчивается выделением системы независимых нулей.

Для этого в первом столбце матрицы выделяется произвольный нуль и отмечается *. Затем рассматриваются нули второго столбца. Если среди них есть такие, которые находятся не в одной строке с нулем первого столбца, отмеченного *, то один из них отмечается *.

Если число независимых нулей равно n, то задача решена. Если меньше, то переходим к общему шагу.

II. Общий шаг.

Целью каждого последующего шага является увеличение числа независимых нулей.

Перед началом итерации выделяются знаком “+” столбцы матрицы, содержащие 0^*. Устанавливаем, имеется ли среди невыделенных элементов матрицы хотя бы один 0.

Возможны два случая:

1. имеется хотя бы один 0.

2. нулей нет.

1. Проверяем, содержит ли строка с невыделенными нулями 0^*. Если да, то невыделенный нуль отмечаем штрихом и эта строка отмечается справа знаком “+” и снимается знак выделения “+” над столбцом. Если нет, то просто отмечаем штрихом и строим цепочку следующим образом: движение начинается от 0^’ по столбцу к 0^*, потом от 0^* к 0^’ по строке. Цепочка заканчивается всегда 0^’.

2. Выбирается среди невыделенных элементов минимальный, и он вычитается из элементов, расположенных в невыделенных строках и прибавляется к элементам, лежащих в выделенных столбцах.

После построения цепочки 0^’ в цепочке обозначается 0^*, а 0^* в цепочке обозначается просто 0. 0^* вне цепочки остается 0^*, 0^’ вне цепочки – просто 0.

Пример 1.

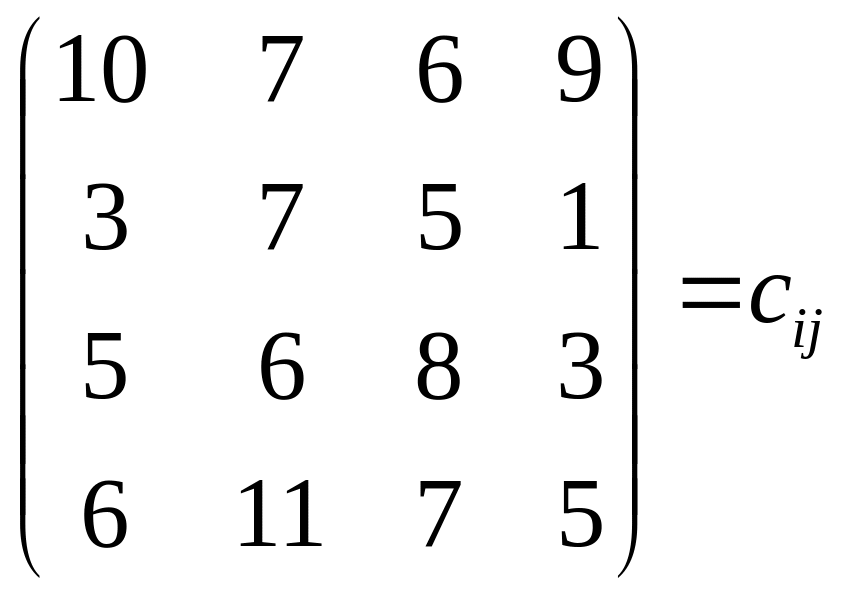max Z

- 4, n=4 => оптимальный план

Ответ:

Пример 2:

max→ переходим на min (умножаем все элементы на -1 и прибавляем число большее максимального элемента в матрице).

выбираем минимальный элемент каждой строки и вычитаем

Вычеркиваем в любом порядке те строки и столбцы, в которых есть нули. Среди невыделенных элементов находят минимум. Его прибавляют к выделенным элементам, а из невыделенных вычитают.

min=3

min=1 min=1

- оптимальный план.