Завдання № 7

Розв'яжіть задачу:

Студентка може витратити на покупку фруктів - апельсинів (X) та яблук

(У)-30 грн. на місяць.

1.Визначте множину наборів фруктів, доступних для студентки, якщо в травні ціна апельсинів становила 5 грн. за кілограм, а яблук - 3 грн.

2.У серпні доход студентки зріс, і тепер вона може витратити на покупку фруктів 60 грн. Яблука подешевшали і коштують 2 грн. за кілограм, а при покупці понад 5 кг апельсинів встановлено знижку, вони продаються за ціною 4 грн. за кілограм.

Визначте, які набори фруктів будуть бюджетно доступними для студентки у серпні. Побудуйте відповідні графіки бюджетного обмеження.

Розв’язання

1) 1.Визначте множину наборів фруктів, доступних для студентки, якщо в травні ціна апельсинів становила 5 грн. за кілограм, а яблук - 3 грн.

Рх = 5 грн/кг

Ру = 3 грн/кг

І = 30 грн.

І = РхQx+PyQy

Нам треба знайти набори товарів х та у, які будуть відповідати бюджету студентки і не перевищуватимуть його. Дані набори товарів визначаємо довільним підбором можливих варіантів починаючи від нуля одиниць першого товару і визначаючи скільки можна придбати іншого і навпаки. Отримані дані вносимо в таблицю і по отриманим координатам побудуємо лінію бюджетних обмежень студентки.

Набори товарів	А	В	С
Х(апельсини), кг	0	3	6
У (яблука), кг	10	5	0

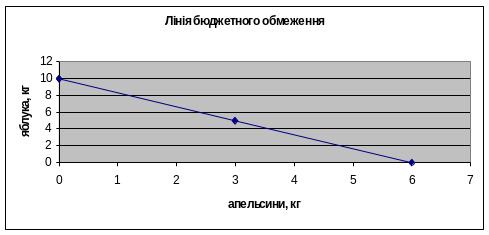
Отже, лінія бюджетного обмеження для студентки на травні місяці побудована.

2) У серпні доход студентки зріс, і тепер вона може витратити на покупку фруктів 60 грн. Яблука подешевшали і коштують 2 грн. за кілограм, а при покупці понад 5 кг апельсинів встановлено знижку, вони продаються за ціною 4 грн. за кілограм.

Дохід студентки зріс вдвічі і становить 60грн. Графічно це відображатиметься переміщенням прямої бюджетного обмеження вверх вправо. Так як маємо подешевшання товару У (яблук) з 3грн./кг до 2 грн./кг то відповідно даного товару можна буде придбати більше ніж вдвічі.

Набори товарів	А	В	С	D	Е
Х(апельсини), кг	0	4	5	6	15
У (яблука), кг	30	20	20	18	0

Для побудови нової лінії бюджетного обмеження визначимо нові контрольні точки але взявши до уваги, що при покупці від 5 кг апельсин, вони коштуватимуть дешевше, а це зобразиться на лінії бюджетного обмеження ще частковим зсувом, який зображено на малюнку нижче.

Отже, як видно з нового графіку, зовнішній вигляд лінії змінився в порівнянні з попередньою. За нового бюджету студентка може вже придбати ту кількість товару, що відображена в таблиці та графічно на новому малюнку.

Завдання № 8

Розв'яжіть задачу:

Фірма збільшує обсяги виробництва продукції у короткостроковому періоді. Заповніть пропуски у наведеній таблиці, обчисливши величини всіх видів продуктів :

Кількість робітників, L	Сукупний продукт, TPL	Граничний продукт, MPL	Середній продукт, APL
3	90	20	30
4	125	105	31,25
5	130	5	26
6	136,5	1,5	22,75
7	136,5	0	19,5

Якщо зафіксувати обсяги використання всіх факторів виробництва, окрім одного (наприклад, праці, обсяг використання якої будемо позначати літерою L), тоді сукупний продукт змінного фактора виробництва (праці — TPL) визначається як обсяг продукції, що виробляє фірма при певному обсязі L використання цього фактора і незмінних обсягах використання всіх інших факторів.

Середній продукт змінного фактора виробництва (праці — APL,) — це відношення сукупного продукту змінного фактора до обсягу фактора, що забезпечив випуск цього продукту:

APL=TPL/L.

Ці показники мають також назву продуктивність праці, продуктивність капіталу.

Граничний продукт змінного фактора виробництва (праці — MPL,) — додатковий випуск продукції, який забезпечується використанням додаткової одиниці ресурсу:

MPL = ATP/AL.

Тут ∆L=L2-L1, - додаткові обсяги ресурсів,

∆ТР=ТР2-ТР1, додатковий випуск, що забезпечується за рахунок ∆L.

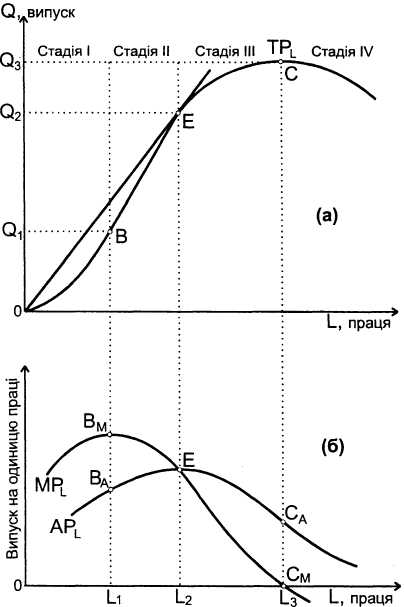
Взаємозв'язок між показниками ГР, АР і МР ілюструє мал., де зображено, як будуть змінюватись криві TPL, APL, MPL при збільшенні обсягу використання праці

Сукупний продукт збільшується разом із збільшенням L до певної межі Q3 у точці С досягає найбільшого зна­чення Q3 при L=L3 а потім зростання припиняється; це є проявом закону спадної віддачі факторів виробни­цтва, згідно з яким при збільшенні обсягу використання певного фактора і незмінних обсягах інших факторів, починаючи з певного моменту (на мал. при L=L1), гранична продуктивність МР цього фактора спадає. Середній продукт зростає, доки L<L2, сягає найбільшого значення у точці Е при L=L2, потім спадає. Граничний продукт зростає, доки L<L1, найбільше його значення досягається в точці Вм при L=L1 потім МР спадає: МРL=0 при L=L3, MPL<0 при L>L3

У залежності від значень МР, АР і ТР, при змінах обсягів праці можна визначити чотири стадії виробництва: стадія І — зростають МР, АР, ТР; ста­дія II — зростають АР, ТР, спадає МР; стадія III — зростає ТР, спадають МР, АР (спадає продуктивність праці, хоча випуск ще збільшується); стадія IV — спадають всі показники.

Закономірним є те, що криві АР та МР на мал. перетинаються в точці Е, де продуктивність праці є максимальною (при L=L2, тобто в цьому випадку досягається найефективніше використання ресурсу. Робимо висновок: якщо гранична продуктивність вища за середню, то продуктивність праці зростає при збільшенні L; якщо гранична продуктивність менша за середню, то продуктивність праці спадає при збільшенні L. Зазначена властивість випливає із загальної властивості співвідношення між середніми та гранич­ними величинами і застосовується для аналізу ефективності використання ресурсів.