5.7. Пример синтеза с минимизацией картами Карно.
В качестве примера использования карт Карно для преобразования неполной таблицы истинности можно рассмотреть реализацию шифратора входных позиционных сигналов «1» в код управления четырехразрядной светодиодной шкалой.
Таблица истинности работы такого шифратора:
-
Входы
Выходы
X4
X3
X2
X1
Y4
Y3
Y2
Y1
0
0
0
0
1
0
0
0
1
0
0
0
1
0
0
0
1
0
0
0
0
0
0
0
1
0
0
0
1
1
0
0
1
1
1
0
1
1
1
1
Таблица, описывающая логику работы шифратора неполная, поскольку содержит только пять строк, соответствующих пяти из 16-ти возможных комбинаций входных сигналов. Это означает, что значения выходных сигналов при неуказанных ситуациях несущественны, так как их не будет на входах.
На Рис.8а, в качестве примера, показана заполненная карта Карно для выхода «Y2.
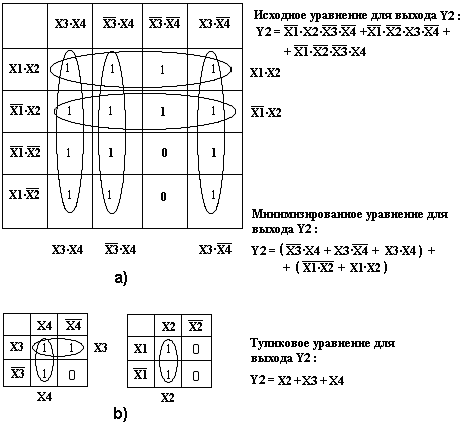
Рис.8
Пять значений пересечений строк и столбцов, заданные таблицей состояний этого выхода, выделены жирным шрифтом.
Остальные значения пересечений, указанные обычным шрифтом, проставлены таким образом, чтобы обеспечить полное «склеивание» выделенных жирным шрифтом значений «1» в своих строках или столбцах. Для этого произведено дополнение этих строк и столбцов значениями «1».
Результат «склеивания» полного столбца проставлен под соответствующим столбцом, а результат «склеивания» полной строки проставлен справа от соответствующей строки.
На Рис.8а «склеиваются» только полные строки и столбцы.
Для дальнейшего преобразования полученного после «склеивания» минимизированного уравнения необходимо использовать или алгебру логики или составить новые карты Карно для составляющих минимизированного уравнения состояний выхода Y2,которые выделены скобками. Эти составляющие имеют только два аргумента.
Преобразовав картами Карно скобки минимизированного уравнения, содержащие пары аргументов, как это показано на Рис.7b, можно получить следующее минимально возможное (тупиковое) уравнение: Y = X2 + X3 + X4.
Вопросы для самопроверки
1. Каковы основные этапы синтеза цифрового комбинационного устройства, и какие условия могут быть поставлены при его синтезе?
2. Каким образом по таблице истинности составляется уравнение состояний выхода цифрового комбинационного устройства в НДФ и НКФ?
3. Каковы два способа минимизации уравнения состояний выхода?
4. Как составляется и заполняется бланк Карты Карно при четном и нечетном числе аргументов уравнения состояний выхода, а также при полной и неполной таблице истинности, описывающей логику цифрового комбинационного устройства?
5. Почему одно и тоже значение «1» в карте Карно может использоваться при «склеивании» нескольких смежных строк и столбцов?
6. Какой результат при преобразовании карты Карно дают следующие строки:
содержащие только значения «1»;
содержащие только значения «0»;
содержащие четное число подряд стоящих значений «1», если остальные значения равны «0»;
содержащие нечетное число подряд стоящих значений «1», если остальные значения равны «0»?
7. Каков простейший вариант реализации логической операции «Исключающее ИЛИ» на базе логических элементов И-НЕ?
8. Какую логику будет иметь схема, соединения в которой соответствуют реализации логической операции «Исключающее ИЛИ» на элементах логических операций И-НЕ (см. Рис.7b), если в ней заменить эти элементы на элементы логических операций ИЛИ-НЕ?