5.6. Пример синтеза цифрового логического устройства.

В качестве примера рассмотрим все пять этапов синтеза простейшего цифрового комбинационного устройства.

Первый этап: словесное описание логики.

Необходимо создать двухвходовое цифровое комбинационное устройство, которое будет сигнализировать о несовпадении сигналов на ее входах, то есть тогда, когда сигналы на его входах имеют противоположные значения. Требуется реализовать устройство с минимальным использованием только логических элементов «И-НЕ».

Второй этап: таблица истинности заданной логики.

Поскольку при словесном описании не задано значение сигнализирующего сигнала, его значением следует задаться перед составлением таблицы истинности.

Например, при сигнализации значением «1» таблица истинности будет иметь следующий вид:

Входы		Выходы
X1	X2	Y
0 1 0 1	0 0 1 1	0 1 1 0

Составленная таблица совпадает с рассмотренной ранее соответствующей таблицей операции «Исключающее ИЛИ».

Третий этап: уравнения состояний выходов.

В примере описывается логика только одного выхода, поэтому таблица состояний устройства описывается одним уравнением.

Для таблицы, составленной на втором этапе, уравнение состояний в виде НДФ для прямого значения функции выхода: .

Для таблицы, составленной на втором этапе, уравнение состояний в виде ^{НДФ для единичного значения функции выхода:} .

^{Можно доказать эквивалентность записи в НДФ и НКФ, преобразовав, например, уравнение в НКФ в уравнение, записанное в НДФ следующим образом:}

.

Четвертый и пятый этапы: преобразование уравнений для выполнения условий синтеза.

В примере поставлены два условия: минимизация и реализация на логических элементах «И-НЕ».

Непосредственный синтез цифрового устройства по уравнениям состояний его выхода, как правило, требует микросхемы, реализующие различные логические операции.

Так, для реализации выхода рассматриваемого в примере устройства по уравнению в виде НДФ потребуется:

• два инвертора для получения инверсных значений входных сигналов;

• две логические двухвходовые логические схемы «И» для реализации произведений прямого значения одного из входных сигналов на инвертированное значение другого входного сигнала;

• одна двухвходовая логическая схема «ИЛИ» для объединения выходов логических схем «И».

На Рис.7а показана функциональная схема устройства, реализованного непосредственно по уравнению состояния его выхода в виде НДФ.

Преобразование этого уравнения может дать многочисленные иные варианты реализации. В частности, можно привести это уравнение к виду, содержащему только логические операции «И-НЕ», что и требуется поставленным заданием.

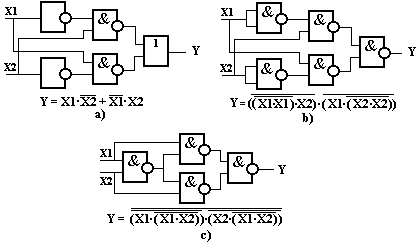
Рис.7

Переход от логической операции сложения к операции умножения (исключить сложение) можно, используя тождество Моргана, следующим образом:

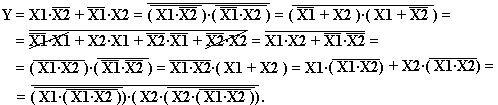
Из полученного в результате преобразования уравнения состояний выхода рассматриваемого в примере устройства следует, что возможны два варианта выполнения поставленного условия реализации на двухвходовых логических схемах «И-НЕ»:

^{- инверсия заменена логической операцией «И-НЕ» над одним и тем же аргументом, на основании тождества X . X = X.}

^{- общая часть, стоящая в скобках и сформированная логической схемой «И-НЕ», одновременно используется для формирования двух инвертируемых произведений, а потому снижает количество требуемых логических схем «И-НЕ».}

На Рис.7b и Рис.7с показаны функциональные схемы, реализующие указанные два варианта использования логических схем «И-НЕ» для реализации логики рассматриваемого устройства.

Рис.7с демонстрирует возможность использования меньшего количества логических схем «И-НЕ», чем в варианте, изображенном на Рис.7b, хотя оба варианта отвечают поставленной задаче.