11.4. Квазистационарные резонаторы

Характерным признаком квазистационарных резонаторов яв­ляется весьма четко выраженное пространственное разделение электрического и магнитного полей у колебания с наименьшей резонансной частотой, т.е. энергия электрического и магнитного полей концентрируется преимущественно в различных частях объема резонатора. Это позволяет рассматривать квазиста­ционарные резонаторы, в которых возбуждается колебание с низшей резонансной частотой, как обычные колебательные кон­туры с сосредоточенными постоянными, причем те части объема, где концентрируется энергия электрического и магнитного полей, эквивалентны соответственно емкостному и индуктивному элемен­там контора. Если величина индуктивного и емкостного сопро­тивлений элементов известна, то резонансная частота квазиста­ционарного резонатора может быть рассчитана по формуле

На рис.11.22 и 11.23 изображены тороидальный резонатор, применяемый в клистронах, и резонатор магнетрона соответственно.

В случае тороидального резонатора электрическое поле почти полностью сосредоточено в зазоре шириной d (рис.11.22). Ем­кость эквивалентного резонансного контура равна емкости зазора между параллельными пластинами резонатора, которая рассчи­тывается по формуле Эта формула является приближенной, так как не учитывает искажение поля на краях конденсатора. Магнитное поле концентрируется преимущественно в боковых полостях резонатора. Если пренебречь неравно­мерностью распределения магнитного поля вдоль оси Z, можно считать, что вектор Н имеет только азимутальную составляющую где /-ток, текущий по боковой поверхности внутрен­него цилиндра, а r-расстояние от оси Z до рассматриваемой точки. Магнитный поток, проходящий через боковые полости резонатора,

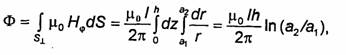
где S_┴ - площадь половины поперечного сечения резонатора, пронизываемая магнитными силовыми линиями. Индуктивность резонатора вычисляется по формуле Зная С_о и Lо, находим угловую резонансную частоту тороидального резонатора:

Аналогично для ячейки магнетронного резонатора {рис.11.23) получаем

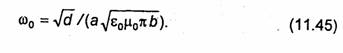
Глава 12

ОБЩАЯ ТЕОРИЯ ЦЕПЕЙ СВЧ

12.1. Понятие об эквивалентной схеме цепи свч. Круговая диаграмма полных сопротивлений

12.1.1. Цепь свч (тракт свч)

Радиосистемы, работающие в диапазоне 30 МГц <f<3000 ГГц, обычно можно представить в виде некоторых устройств, соеди­ненных отрезками линий передачи. Часть такой системы, распо­ложенную между начальным и оконечным устройствами (напри­мер, между антенной и радиопередающим или радиоприемным устройством), называют трактом СВЧ или цепью СВЧ. Подобный тракт осуществляет передачу электромагнитной энергии от пере­датчика к антенне или от антенны к приемнику, обеспечивает тре­буемый режим работы выходных или входных цепей передатчика или приемника, выполняет частотное и поляризационное разделе­ние и объединение передаваемых сигналов и ряд других функций. Отметим, что цепью СВЧ называют также и отдельные части трак­та СВЧ. Наиболее распространенными элементами СВЧ цепей являются отрезки линий передачи, переходные и стыковочные уз­лы между линиями разных типов, согласующие и настроечные элементы, сумматоры, делители и ответвители мощности, поляри­зационные устройства, фильтры, фазовращатели, коммутаторы и переключатели, невзаимные устройства с намагниченными фер­ритами и др. Перечисленные и некоторые другие элементы СВЧ рассмотрены в последующих главах.

Процессы передачи электромагнитных сигналов в цепях СВЧ и в образующих их элементах являются весьма сложными. Их можно было бы проанализировать на основе решения соответст­вующих краевых задач электродинамики. Однако строгая поста­новка и решение таких задач даже для сравнительно простых эле­ментов цепей СВЧ возможны далеко не всегда. А для применяе­мых на практике цепей СВЧ из-за их конфигурационной сложности решение краевых задач в строгой постановке в настоящее время практически невозможно. На практике при анализе сложных цепей СВЧ применяют метод декомпозиции (разбиения): цепь СВЧ разбивается на ряд элементов, которые анализируются независимо. При этом каждый такой элемент рассматривается как независимая электродинамическая система.

Постановка и решение краевых задач, соответствующих от­дельным элементам, существенно проще, чем для всего устройст­ва в целом. Используя или решение электродинамической задачи или результаты экспериментального исследования, если подобное решение получить не удается, для каждого выделенного элемента строят такое описание, которое позволяет находить влияние этого элемента на передаваемые электромагнитные сигналы. Обычно описание элементов цепи представляют либо в виде одной из матриц (матрицы рассеяния, матрицы передачи и др.), либо в виде эквивалентной схемы, состоящей из отрезков эквивалентной ли­нии передачи, в которую тем или иным способом включены сосре­доточенные элементы L, С, R и трансформаторы. Имея подобные универсальные описания всех элементов цепи СВЧ, можно опре­делить все требуемые характеристики цепи (см. 12.3).

Обычно при построении математической модели цепи СВЧ для упрощения анализа отрезки линий передачи, соединяющие входящие в эту цепь устройства, заменяют отрезками эквивалент­ной линии, а устройства рассматриваются как некоторые многополюсники. Электромагнитные процессы в эквивалентной линии опи­сываются скалярными функциями (напряжением 0_т и током i_т), зависящими лишь от продольной координаты z. Эти функции стро­ятся на основе векторных функций Ё_т и Н_т, определяемых для каждой линии из решения соответствующей электродинамической задачи (см. гл.10). Отметим, что указанную упрощенную модель отрезка линии передачи можно использовать лишь в диапазоне частот, где соблюдается одноволновый режим работы линии. Кро­ме того, эта модель непригодна для определения ряда характери­стик цепи СВЧ, например таких, как максимальная мощность, пе­редаваемая по цепи СВЧ, или величина взаимной связи между элементами цепи СВЧ, построенной на отрезках линий передачи открытого типа, и некоторых других.

Рассмотрим переход к эквивалентной линии. Для TЕМ-волн в линиях передачи, структура поля которых в поперечной плоскости имеет потенциальный характер, можно, используя векторы Ё_т и Н_т, однозначно определить соответствующие им напряжение 0_т и ток i_т. При этом для волны, распространяющейся по линии без потерь вдоль оси Z, можно записать

где k- коэффициент фазы рассматриваемой волны.

В гл.10 были определены U_m(z) и l_m(z) для TЕМ-волн в двух­проводной и коаксиальной линиях. Зная функции (12.1), можно вы­числить волновое сопротивление линии Z_B = U_m(z)/i_m{z) и сред­нюю за период мощность, переносимую волной по линии:

Для линии передачи, в которой распространяются Е-, Н- или смешанные волны, напряжение и ток в эквивалентной линии могут быть выражены через контурные интегралы от функций E_m┴ и Н_т┴ соответственно; указанные функции описывают попе­речные составляющие полей в рассматриваемой линии передачи. В отличие от случая TЕМ-волн у Е-, Н- и смешанных волн поле, описываемое функциями Ё_т┴ и Н_т┴ не является потенциальным. Поэтому значения функций U_m(z) и i_m(z) определяются неодно­значно: они зависят от выбора контуров интегрирования. Для уст­ранения этой трудности при переходе к эквивалентной линии за­ранее оговаривают форму указанных контуров. Рассмотрим, как вычисляются напряжение, ток и волновое сопротивление для вол­ны Н₁₀, бегущей вдоль оси Z прямоугольного волновода. Исполь­зуя выражение (10.18) для составляющей Ё_ту волны Н₁₀, опреде­ляем комплексную амплитуду напряжения между точками, лежа­щими на средних линиях широких стенок при х = а/2:

Изменив форму контура либо методику определения напря­жения и тока, можно получить другие выражения для Z_B. Однако во всех случаях формула для имеет вид где А-числовой коэффициент, зависящий от способа вычисления ве­личин Неопределенность в выборе этого коэффи­циента существенного значения не имеет, так как при инженерном проектировании цепей СВЧ важно знать отношение волновых со­противлений соединяемых отрезков линий, а не конкретные значе­ния каждого из них.

На основе изложенного любую линию передачи можно заме­нить эквивалентной длинной линией, в которой распространяются соответствующие волны напряжения и тока. Отметим, что матема­тическую модель в виде эквивалентной линии можно использовать и для линии передачи, в которой могут распространяться несколь­ко типов волн. В этом случае для каждого распространяющегося по линии типа волны с помощью формул, аналогичных (12.3)—(12.5), строится своя эквивалентная линия, т.е. математическая модель образуется несколькими (по числу распространяющихся типов волн) эквивалентными линиями.