Глава 11

ОБЪЕМНЫЕ РЕЗОНАТОРЫ

11.1. Общие свойства объемных резонаторов

11.1.1. Общие сведения

На низких частотах в качестве колебательного контура (резо­натора) широко применяется параллельное соединение сосредо­точенных индуктивности и емкости. Колебательный процесс в та­кой системе возникает, как известно, в результате непрерывного обмена энергией между электрическим полем, сосредоточиваю­щимся в конденсаторе, и магнитным полем, сосредоточивающим­ся в индуктивности. В диапазоне СВЧ создание контуров из сосре­доточенных элементов с малыми потерями и соответственно вы­сокой добротностью практически невозможно. Поэтому в этом диапазоне применяют преимущественно колебательные системы из элементов с распределенными параметрами (отрезки двухпро­водной, коаксиальной линий, волноводов и др.).

Возможность построения таких систем вытекает из уравнений Максвелла. Действительно, согласно этим уравнениям перемен­ное электрическое поле является источником переменного маг­нитного поля, а переменное магнитное поле, в свою очередь, воз­буждает переменное электрическое поле, и т.д., т.е. обмен энерги­ей между электрическим и магнитным полями происходит непре­рывно в любой области пространства. Если каким-либо образом устранить излучение электромагнитных волн из некоторой области пространства и добиться отсутствия тепловых потерь, то обмен энергиями должен протекать сколь угодно долго. Это означает, что в изолированном от внешнего пространства объеме, заполненном средой без потерь, может существовать, как и в обычном резо­нансном контуре без потерь, незатухающий колебательный про­цесс. Подобные резонансные системы получили название объем­ных резонаторов.

Простейшие типы объемных резонаторов представляют собой часть пространства, ограниченную со всех сторон металлической оболочкой. Сюда, в частности, относятся резонаторы в виде короткозамкнутых отрезков коаксиальной линии, полых металлических

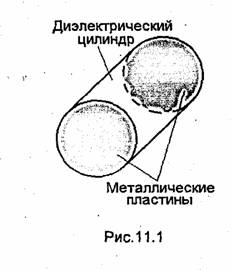
Волноводов и др. По аналогии с направ­ляющими системами резонаторы этого типа называют закрытыми. Можно также почти полностью устранить излучение в окружаю­щее пространство, используя явление пол­ного отражения от границы раздела двух диэлектриков с различными диэлектриче­скими проницаемостями. В качестве приме­ра на рис.11.1 показан объемный резонатор этого типа, представляющий собой отрезок диэлектрического волновода, торцы которого металлизированы. По аналогии с направляющими системами ре­зонаторы, в которых отсутствует замкнутая металлическая обо­лочка, называют открытыми.

11.1.2. Свободные гармонические колебания в объемных резонаторах

Предположим, что в объеме V_o (в произвольном резонаторе) тепловые потери равны нулю и, кроме того, отсутствует обмен энергией между внешним пространством и внутренним объемом резонатора. Уравнение баланса (1.126) при этих условиях име­ет вид

Р^ст =dWldt. (11.1)

Под влиянием источника в объеме V_o возникнут электромаг­нитные колебания. Пусть через некоторое время сторонний источ­ник отключается. При этом за счет запасенной в резонаторе энер­гии колебательный процесс будет продолжаться сколь угодно дол­го и при отсутствии источников. В резонаторе возникнут свободные или, другими словами, не связанные со сторонним источником электромагнитные колебания. При Р^ст = 0 из (11.1) получаем

dWdf = O, (11.2)

т.е. в соответствии с законом сохранения энергии полная энергия, запасенная в изолированном от внешнего пространства объеме, при отсутствии потерь в любой момент времени остается постоян­ной. Однако соотношение величин электрической и магнитной энергий в общей неизменной сумме непрерывно меняется ввиду обмена энергией между переменными электрическим и магнитным полями. В общем случае изменение во времени напряженности электрических и магнитных полей в резонаторе носит негармони­ческий характер. Особый интерес представляет случай, когда свободные колебания являются гармоническими. Пусть, например, Е = Ei sin ω_ot, где E₁ - функция, зависящая от пространственных координат, а ω_о - угловая частота свободных колебаний. В момент t = 0 напряженность электрического поля равна нулю. Равна нулю в этот момент и энергия, запасенная в электрическом поле. Но полная энергия в объеме V_o резонатора, как следует из (11.2), не зависит от времени. Следовательно, в момент t = 0 у рассматри­ваемого свободного колебания вся энергия сосредоточена в маг­нитном поле, что при гармонических колебаниях означает наличие фазового сдвига, равного π/2, между векторами Е и Н, т.е. Н = H₁ cos ω_ot, где Н₁ - функция пространственных координат. Пе­реписывая (11.2) для гармонических колебаний с учетом формул (1.130)-( 1.132), получаем