10.7.6. Световоды

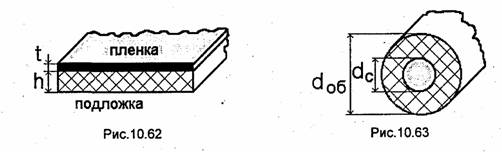
В настоящее время наибольшее применение на практике для передачи оптических сигналов находят пленочные и волоконные световоды. Основу пленочного световода (рис.10.62) составляет диэлектрическая пленка с параметрами ε_пл, μ_о, выращенная на диэлектрической подложке или сформированная методами интег­ральной технологии. Подложка имеет параметры ε₁, μ₀; параметры среды над пленкой ε₂, μ_о- Отметим, что чаще оптические не­магнитные среды описываются с помощью коэффициента прелом­ления п =√ε_r, при этом предполагается, что магнитная прони­цаемость у всех рассматриваемых сред одинакова и равна μ₀. Пленку можно рассматривать как плоский диэлектрический вол­новод (см.10.7.3). Для распространения волн по такому волноводу необходимо, чтобы n_пл>n₁ и п_пл>п₂. Подобные световоды ис­пользуются для передачи света на небольшие расстояния, как правило, в пределах интегральной схемы оптического диапазона.

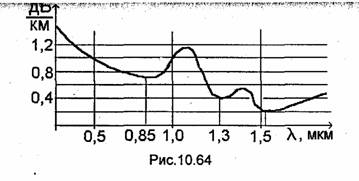
Волоконный световод состоит из диэлектрических сердечника и оболочки, диаметры которых равны d_c и d_oб соответственно (рис. 10.63). Коэффициенты преломления сердечника и оболочки равны п_с и n_о6, причем п_с>п_об. Для защиты от внешних воздействий и повышения механической прочности световода на наружную поверхность оболочки наносят полимерное покрытие (на рисунке покрытие не показано). В данном случае полное внутреннее отражение парциальных волн, распространяющихся в сердечнике, происходит на границе между сердечником и оболочкой. Воз-

никающая при этом поверхностная волна распространяется в оболочке. Поэтому энергия, переносимая волнами по световоду, сосредоточена в сердечнике и оболочке. На оболочку можно наносить поглощающее покрытие, не влияющее на распрост­раняющиеся по световоду волны и поглощающее энергию волн излучения, возникающих в световоде при его возбуждении источ­ником (см. 15.2).

Обычно в качестве диэлектрика, из которого изготавливают сердечник световода, используют стекло, иногда для этой цели применяют различные полимеры. В качестве материала оболочки, как правило, также используют стекло, иногда полимеры [28]. Показатель преломления оболочки постоянен, а показатель пре­ломления сердечника может быть как постоянной величиной, так и функцией поперечной координаты. В настоящее время получены волоконные световоды на основе кварцевого стекла, легиро­ванного германием, фосфором или бором, с достаточно малыми потерями в некоторых областях оптического спектра, называемых окнами прозрачности. На рис.10.64 показана типовая зависимость затухания в таком световоде, выраженная в дБ/км. Как видно из графика, существуют три окна прозрачности для распростра­няющихся по световоду сигналов λ≈0,85 мкм, λ≈1,3 мкм и λ≈1,5 мкм. Эти частотные диапазоны, как правило, и используют для передачи оптических сигналов по световодам.

По волоконному световоду, как по диэлектрическому волно­воду, могут распространяться E-, Н- и гибридные волны. Поскольку критические частоты волн в диэлектрическом волноводе, как следует из результатов, полученных в 10.7.5, зависят не только от величины d_c, но и от разницы коэффициентов преломления

то, выбирая достаточно близкие по величине п_с и n_об,

можно обеспечить одноволновый или близкий к нему режим работы световода при достаточно больших значениях d_c (много больших длины волны): Последнее обстоятельство весьма существенно из-за очень малой длины волны светового излучения

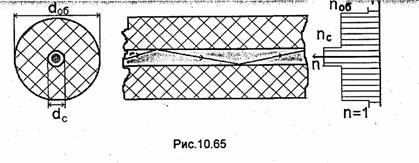
(λ≈1 мкм). Как правило, применяемые на практике одноволновые световоды или, как их называют в литературе, одномодовые световоды, работающие на основной волне диэлектрического волновода, имеют d_c≈ 3...5 мкм и d_Об≈50 мкм, при этом величины п_с и n_об отличаются не более чем на 3%. На рис. 10.65 показаны поперечное и продольное сечения такого световода; на про­дольном сечении изображены парциальные волны, соответст­вующие распространяющейся по световоду волне. На этом же рисунке изображено распределение вдоль радиуса коэффициента преломления сред, образующих световод. Одномодовый световод, как и любой диэлектрический волновод, обладает дисперсией, поскольку и фазовая скорость основной волны зависит от частоты и величина коэффициента преломления стекла является функ­цией частоты. Дисперсия ограничивает полосу передаваемых по световоду частот, т.е. вносит искажения в передаваемые сигналы. Если на вход световода подать сигнал в виде импульса, то по мере распространения этот импульс будет расширяться, причем величина расширения зависит как от степени дисперсии, так и от длины пути, проходимого сигналом по световоду. Расширение импульса эквивалентно сужению полосы пропускания световода и часто оценивается эквивалентной шириной полосы пропускания, выраженной в мегагерцах на километр [МГц/км]. При передаче импульсных сигналов обычно такое искажение сигналов оцени­вается величиной километрического уширения, выраженной в наносекундах на километр [Нс/км]. Расчеты и эксперименты показывают [28], что изготовленные на основе кварцевого стекла одномодовые световоды имеют минимальную дисперсию в об­ласти λ≈ «1,3...1,4 мкм. В этой области такие световоды имеют наибольшую полосу пропускания.

Весьма малые поперечные размеры сердечника одномодовых световодов вызывают достаточно серьезные трудности при их изготовлении, что сильно удорожает производство. Кроме того, малый диаметр сердечника затрудняет эффективный ввод мощ­ности от источника в световод и предъявляет весьма жесткие требования к устройствам соединения таких световодов. Как правило, для возбуждения одномодовых световодов приходится использовать дорогостоящие полупроводниковые лазеры [23]. Поэтому одномодовые световоды применяют в случае, если требуется передавать значительные объемы информации на достаточно большие расстояния (более нескольких сотен или тысяч километров).

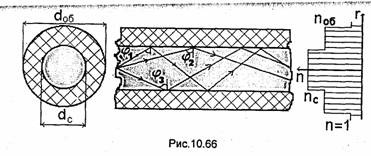
Для передачи небольших объемов информации на не очень большие расстояния (несколько десятков километров) используют многомодовые световоды, имеющие, как правило, d_c≈50 МКМ и d_cб ≈ 120MKM (рис.10.66). Изготовление таких волокон гораздо проще и дешевле. Увеличение диаметра сердечника по сравнению с диаметром сердечника одномодового световода обеспечивает два преимущества: возможность работы таких световодов с достаточно простыми и дешевыми некогерентными источниками излучения (светодиодами) и менее жесткие требования к уст­ройствам соединения световодов. Из-за значительной величины d_c по многомодовому световоду может распространяться множество различных типов волн (порядка 1000), которые и переносят передаваемые по световоду сигналы. Каждую из распростра­няющихся волн можно представить парциальными волнами (лу­чами), движущимися под определенным углом к нормали к границе раздела сердечник - оболочка. На рис.10.66 показаны три луча, соответствующие трем волнам, распространяющимся по волокну,

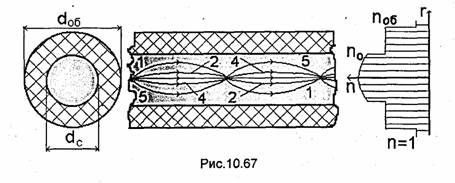
Для сохранения достаточно большого диаметра сердечника (как у многомодового волокна) и одновременного уменьшения величины модовой дисперсии на практике применяют так назы­ваемые градиентные световоды (рис. 10.67). Такие световоды имеют, как правило, d_c ≈50 мкм и d_Oб≈80 мкм. Сигнал по таким световодам передается многими типами волн. Для уменьшения величины модовой дисперсии используют сердечник, коэффи­циент преломления которого является функцией поперечной координаты r и, как правило, описывается формулой

где ∆ = (п₀-п_об)/п₀, п₀ - величина коэффициента преломления на оси сердечника, q- целое положительное число. Коэффициент преломления уменьшается от значения п₀ (на оси сердечника) до значения л_об на границе с оболочкой.

Как следует из законов Снеллиуса, если плоская волна падает на границу раздела двух сред из более плотной среды (n₁>n₂) под углом φ (или под углом 90°- φ к границе раздела), то направление распространения преломленной волны будет составлять с грани­цей раздела угол меньший, чем 90°-φ, поскольку в этом случае θ > φ. Если же падающая плоская волна распространяется в менее плотной среде {п₁<п₂), то направление распространения прелом­ленной волны будет составлять с границей раздела угол больший, чем 90°-φ. На этом основании можно утверждать, что если плоская волна движется в среде с плавно изменяющейся вели­чиной коэффициента преломления под некоторым углом к нап­равлению изменения величины п, то в общем случае направление распространения волны будет плавно искривляться. Поэтому в градиентном волокне траектории лучей, соответствующих различным типам волн и направленных под разными углами к оси сердечника, будут криволинейными (рис. 10.67): чем больший угол с осью составляет направление луча, тем по более длинной траектории он перемещается, и наоборот. Однако луч, распрост­раняющийся по самой длинной траектории, будет иметь самую высокую среднюю фазовую скорость, поскольку его траектория проходит через области сердечника с самым низким значением коэффициента преломления (вблизи оболочки). Напомним, что фазовая скорость плоской волны обратно пропорциональна вели­чине п среды. В свою очередь, луч, распространяющийся вдоль оси сердечника, имеет самую низкую фазовую скорость, поскольку его траектория проходит в области сердечника с самым высоким значением n. Фазовый сдвиг, получаемый каждым лучом при прохождении конечного отрезка волокна, прямо пропорционален длине траектории и обратно пропорционален средней фазовой скорости луча. Поэтому выбором величины q в (10.89) можно в значительной степени уменьшить разность фазовых сдвигов, получаемых разными лучами при прохождении конечного отрезка волокна, т.е. уменьшить разность фазовых скоростей различных волн в градиентном волокне.

Наиболее часто на практике применяют градиентные волокна с q = 2, которые называют параболическими. Такие волокна по сравнению с многомодовыми имеют значительно меньшую вели­чину модовой дисперсии, что приближает их к одномодовым волокнам [23].