7.5.2. Диэлектрик и идеальный проводник

Все выводы данного раздела получены в предположении, что обе среды являются идеальными диэлектриками. Тем не менее полученные выражения позволяют также исследовать случай, когда первая среда - диэлектрик, а вторая - идеальный про­водник. Как уже отмечалось, Z_c для идеального проводника равно нулю. Поэтому для перехода к случаю падения плоской волны из диэлектрика с параметрами ε и μ на плоскую идеально прово­дящую поверхность нужно в окончательных формулах положить Z_c2 = 0. При этом

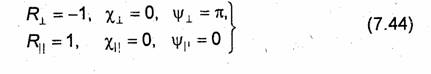
при любом угле падения φ. Следовательно, полное отражение от поверхности идеального проводника имеет место при любых углах падения. Поле во второй среде тождественно равно нулю, а в первой представляет собой направляемую волну, распростра­няющуюся вдоль границы раздела (вдоль оси Z).

На границе раздела (при х = 0) в рассматриваемом частном случае должно выполняться граничное условие Ё_ту ׀_х=0 = 0. Легко убедиться что оно выполняется. Действительно, подставляя (7.44) в (7.37) и полагая n = 0, получаем х₀ = 0. Это означает, что первая плоскость, на которой Е_ту = 0, совпадает с границей раздела.

Фазовая скорость, длина волны Λ и скорость распространения энергии в этом случае такие же, как при полном отражении от границы раздела двух диэлектриков, и определяются формулами (7.30), (7.32) и (7.39) соответственно. Структура поля вдоль оси Х также имеет характер стоячей волны с длиной λ _х, определяемой выражением (7.34).

7.6. Падение плоской волны на границу поглощающей среды

Пусть плоская волна падает под углом φ на плоскую границу раздела двух сред, из которых первая - идеальный диэлектрик, а вторая обладает проводимостью. Общие формулы, определяю­щие поля падающей, отраженной и преломленной волн, можно использовать и в этом случае, если считать в них параметры k₂ и Z_c2 комплексными величинами. Из второго закона Снеллиуса (7.11) следует, что при этом sin 8 становится комплексным, так как k₁ и sin φ - действительные числа, а k₂ = k₂ комплексная величина.

Это означает, что параметр θ нельзя рассматривать как геометрический угол, под которым распространяется прелом­ленная волна. Введем обозначения

и х = const соответственно. Сле­довательно, волна (7.46) явля­ется неоднородной плоской во­лной. Направление распрост­ранения этой волны образует некоторый угол θ_Д с осью X, который называют истинным (или действительным) углом преломления (рис.7.7). Поверх­ности равных фаз представляют собой параллельные плоскости, нормаль к которым образует с осями X и Z углы θд и π/2-θд соответственно. Уравнение,

определяющее такие плоскости, может быть также записано в виде х cos θ_Д + z sin θ_Д = const. Сравнивая это равенство с уравнением (7.47), находим, что

Отметим, что в рассматриваемом случае ПРФ повернуты относительно ПРА на угол θ_Д (см. рис.7.7).

Амплитуды векторов Е и Н экспоненциально убывают в направлении нормали к поверхности раздела (вдоль оси X). Имеется продольная по отношению к направлению распростра­нения преломленной волны составляющая вектора Н (в случае нормальной поляризации) или продольная составляющая вектора Е (в случае параллельной поляризации).

Поле в первой среде складывается из падающей и отра­женной волн и не имеет принципиальных отличий от поля, воз­никающего при отражении волны от границы раздела двух ди­электриков.

Аналогичные результаты можно получить, анализируя случай параллельной поляризации.

Практически важным является случай, когда вторая среда оптически намного плотнее первой:

Это означает, что при любом угле падения ср на поверхность хорошо проводящей среды преломленная волна распространяется практически вдоль нормали к поверхности раздела. Поверхности равных фаз и поверхности равных амплитуд при этом практически совпадают, и волну можно считать однородной. Продольная по отношению к направлению распространения составляющая век­тора Н (или, в случае параллельной поляризации, вектора Ё)будет пренебрежимо мала по сравнению с поперечной состав­ляющей. Можно считать, таким образом, что волна является поперечной, причем векторы Е и Н, в ней сдвинуты по фазе друг относительно друга на угол Иными словами, при анализе плоской волны, возникающей в результате пре­ломления на поверхности хорошо проводящей среды, можно использовать все основные соотношения, полученные в 6.1.4 при исследовании свойств плоской волны, свободно распростра­няющейся в хорошо проводящей безграничной однородной изо­тропной среде.

Подчеркнем, что амплитуды векторов Е и Н преломленной волны в металле быстро убывают с удалением от границы раздела и волна фактически существует лишь в тонком слое вблизи поверхности раздела.