6.1.2. Свойства плоской волны в однородной изотропной среде

Исследуем основные свойства плоской волны, распростра­няющейся в безграничной однородной изотропной среде. Источни­ки, создающие волну, находятся за пределами рассматриваемой области. Поэтому векторы Ё_т и Н_т удовлетворяют однородным уравнениям Гельмгольца (2.33) и (2.34) соответственно. Предпо­ложим, что поле не зависит от координат х и у. Тогда уравнения (2.33) и (2.34) принимают вид

Рассматривая таким же образом фазу напряженности элек­трического поля волны 2), придем к равенству ω∆t=-β∆z. В этом случае положительным ∆t соответствуют отрицательные значения ∆z, то есть волна 2) распространяется противоположно оси Z.

Предположим, что источник, создающий электромагнитное поле, расположен со стороны отрицательных значений z (рис. 6.1). Так как среда считается безграничной и однородной, в рассматри­ваемой области пространства должна существовать только волна, распространяющаяся в положительном направлении оси Z. По­этому в первом слагаемом в формуле (6.4) в соответствии с выбо­ром вида множителя exp(-i kz) следует положить

В среде без потерь и формулы (6.13) переходят в (6.1).

При изменении удельной проводимости от нуля до беско­нечности угол ψ_с увеличивается от нуля до π/4, а модуль Z_c убывает от до нуля. Как видно, наличие потерь приводит к уменьшению абсолютной, величины характеристического сопро­тивления, т.е. к увеличению | Н | при заданном значении | Е |. Это обусловлено тем, что величина Н определяется как током про­водимости, так и током смещения. В среде без потерь существуют только токи смещения. В среде с потерями при тех же значениях Е и ε токи смещения остаются прежними, но к ним добавляются токи проводимости.

Проанализируем полученные результаты. Рассмотрим снача­ла случай, когда вектор. Ё_m имеет лишь одну составляющую, например, Ё_хт. Тогда вектор Н_т также будет иметь одну сос­тавляющую, перпендикулярную Е_т (в рассматриваемом примере Н_ут). Считая вектор Ё_о вещественным (Ё₀=х₀Е₀) и переходя к мгновенным значениям векторов Е и Н из (6:13) получаем

Из полученных формул видно, что поле плоской волны в однородной изотропной среде обладает следующими свойствами.

Волна является поперечной. Комплексные амплитуды (Ё_т и Н_т) векторов Е и Н всегда взаимно перпендикулярны, а в частном случае, когда вектор Ё_о имеет одну составляющую (например, Ё_о =х_оE_о), взаимно перпендикулярны и их мгновенные значения. Более подробно вопрос о перпендикулярности мгновенных значе­ний векторов Е и Н рассмотрен в 6.2. Поверхности равных фаз определяются уравнением z = const и представляют собой се­мейство плоскостей, перпендикулярных оси Z. Амплитуды векто­ров Е и Н экспоненциально убывают вдоль оси Z. Постоянную а называют коэффициентом ослабления. В среде без потерь α= 0 и

амплитуды векторов Е и Н не зависят от координат. При σ≠0 поверхности равных амплитуд (ПРА) совпадают с ПРФ. Волны, обладающие таким свойством, как и волны, амплитуды векторов Е и Н которых не зависят от координат, называют однородными. При

σ≠0 между векторами Е и Н имеется фазовый сдвиг. Вектор Н опаздывает по фазе относительно вектора Е на угол В среде без потерь векторы Е и Н изменяются синфазно. При изменении а от нуля до бесконечности фазовый сдвиг возрастает от нуля до π/4. На рис. 6.2 и 6.3 показаны зависимости мгновенных значений векторов Е и Н от времени tв некоторой фиксированной точке пространства (z = z₀) в среде с σ≠0 (см. рис. 6.2) и в среде без потерь (см. рис.6.3). На рис.6.4 и 6.5 показаны зависимости тех же величин от координаты z в некоторый фиксированный момент

времени t=t₀ для случаев σ≠0 (см.рис.6.4) и σ =0 (см. рис. 6.5).

Фазовая скорость v_ф плоской волны находится так же, как в случае сферической волны (см.5.3). Используя формулу (6.13), рассмотрим перемещение ∆z ПРФ за время ∆t. В результате придем к равенству из которого следует, что при σ≠0

В среде без потерь т.е. равна скорости света в среде с теми же параметрами ε и μ. Так как то v_ф в среде с потерями меньше у_ф в среде без потерь с теми же ε и μ.

Параметр β, определяющий фазовую скорость, называют коэффициентом фазы. Как видно из (6.16), при σ≠0 фазовая скорость зависит от частоты (tg δ =σ/(ωε)): с увеличением пос­ледней она возрастает. Предельное значение v_ф при ω→∞ равно

Кроме того, величина v_ф зависит от проводимости сре­ды: при одинаковой частоте она будет меньше в среде с большей проводимостью.

Она меньше длины волны в среде без потерь с теми же ε и μ. Ее значение зависит от проводимости среды. При фиксированной частоте длина волны λ убывает с увеличением σ; при σ = О длина волны

Распространение волны сопровождается переносом энергии. При σ≠0 комплексный вектор Пойнтинга

содержит как действительную, так и мнимую часть. Это означает, что имеется как активный, так и реактивный поток энергии. Средняя за период плотность потока энергии экспоненциально убывает вдоль оси Z:

При σ≠0 комплексный вектор Пойнтинга является чисто действительным и не зависит от координат:

Как видно, в этом случае имеется только активный поток энергии.

Возникновение реактивного потока энергии в среде с σ≠0 может быть объяснено следующим образом. При распространении электромагнитной волны в среде возникают электрические токи с плотностью j = σЕ, на поддержание которых расходуется часть энергии волны. В свою очередь, возникшие в среде электрические токи, излучают электромагнитное поле: создают вторичную плос­кую волну, которая складывается с первичной, происходит непре­рывный обмен энергией между волной и средой, что и приводит к возникновению реактивного потока энергии.

Скороcть распространения энергии вычисляется по формуле (1.162) и равна фазовой скорости:

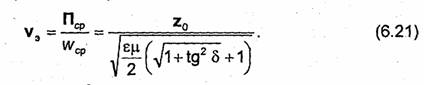
Как видно, при σ≠0 скорость распространения энергии за­висит от частоты. В среде без потерь одинакова при любой частоте.

Характеристическое сопротивление волны Z_c при σ≠ 0 также

зависит от частоты. Модуль Z_c возрастает с увеличением f. Его

предельное значение при f→∞ совпадает с характеристическим сопротивлением волны, распространяющейся в среде без потерь с теми же ε и μ, т.е. равно Аргумент характеристического сопротивления ψ_с изменяется от π/4 (при f→0 ) до нуля (при f→∞).

Из изложенного следует, что свойства плоской волны, рас­пространяющейся в среде с проводимостью и в среде без потерь, различны. Основное отличие состоит в том, что в среде без потерь параметры плоской волны (v_ф, v₃, a, Z_c и др.) одинаковы при любых частотах, а в среде с проводимостью они зависят от частоты. Зависимость свойств волны от частоты называется дисперсией, а соответствующие среды - диспергирующими. Отметим, что среда может быть диспергирующей и при σ = 0, если характеризующие ее параметры е и ц зависят от частоты.

В общем случае вектор Ё_т имеет две составляющие Ё_хт и Ё_ут, между которыми возможен фазовый сдвиг. При этом вектор Н_т также будет иметь две составляющие Н_хт и Н_ут. Если сос­тавляющие вектора E по осям X и Y (Е_х и E_у) изменяются синфазно, то поворотом осей координат X и У вокруг оси Z этот случай сводится к уже рассмотренному, когда вектор Ё_т имеет одну составляющую. При наличии между составляющими Ё_хт и Ё_ут фазового сдвига, не равного n_π, где п - целое число, волна имеет некоторые особенности, например при f→0 мгновенные значения векторов Е и Н не являются взаимно перпендикулярными (см.6.2). Перечисленные выше остальные свойства плоской волны имеют место и в этом случае.

Рассмотрим два частных случая реальных сред: диэлектрики и проводники.