3.5. Постановка и методы решения задач электростатики

3.5.1. Определение поля, создаваемого известными источниками в безграничной однородной среде

Прямая задача электростатики заключается в определении векторов поля по заданному распределению зарядов. При этом область пространства, в которой требуется определить поле, может быть как ограниченной, так и неограниченной.

Наиболее просто такая задача решается в том случае, когда рассматриваемая область представляет собой неограниченное пространство, заполненное однородной изотропной средой, а за­ряды сосредоточены внутри некоторого объема конечных размеров (т.е. отсутствуют заряды в бесконечно удаленных точках). Математически она формулируется следующим образом. Задана объемная плотность заряда ρ как функция координат. Требуется найти функцию и, удовлетворяющую уравнению Пуассона (3.7) и обращающуюся в нуль в бесконечно удаленных точках. Эта задача была рассмотрена в 2.5.2 и 3.2. Ее решением является выражение (3.9). Если заряды распределены на поверхности конечных раз­меров S с плотностью ρ_s, то соответствующий им потенциал опре­деляется формулой (3.10). Если же поле создается зарядами, распределенными с линейной плотностью τ вдоль контура конеч­ных размеров Г, искомая функция и определяется выражением (3.11).

В тех случаях, когда система зарядов не может быть охвачена описанной вокруг начала координат сферой конечного радиуса, т.е. содержит заряды в бесконечно удаленных точках (например, бесконечно длинная заряженная нить), то формулы (3.9)—(3.11) могут оказаться непригодными. Это, в частности, имеет место при решении так называемых плоских задач электростатики, т.е. при одинаковом распределении зарядов (и поля) в любой плоскости, перпендикулярной к некоторой прямой линии, например к одной из осей декартовой системы координат. Такую систему зарядов можно представить как бы состоящей из тонких, равномерно заряженных по длине бесконечно протяженных прямолинейных нитей. Поэтому для определения поля, создаваемого подобной системой зарядов, нужно знать потенциал, создаваемый одной нитью.

Пусть имеется бесконечно тонкая равномерно заряженная с плотностью τ = const нить. Введем цилиндрическую систему ко­ординат τ, φ, z, ось Z которой совпадает с нитью, и рассмотрим поток вектора D через поверхность кругового цилиндра радиуса а и длиной Δl, ось которого совпадает с осью Z (рис. 3.4). Из условия задачи очевидно, что поле должно обладать осевой симметрией, а векторы Е и D должны быть перпендикулярны к боковой поверхности цилиндра. Поэтому поток вектора D через основания цилиндра отсутствует, а поток через боковую поверхность равен D∙2πrΔl. Используя теорему Гаусса (1.40) и учитывая, что полный заряд внутри рассматриваемого цилиндра равен τΔl, получаем

где r₀-орт радиуса-вектора цилиндрической системы координат. Поскольку в рассматри­ваемом случае поле не зависит от переменных φ и z (производные потенциала и по переменным φ и z равны нулю), то из определения электростатического потенциала (3.2) и формулы (3.38) имеем

где В - произвольная постоянная. Обычно постоянную В полагают равной нулю и потенциал нити определяют выражением

Если вместо нити имеется тонкий бесконечно длинный ци­линдр с площадью поперечного сечения ΔS, равномерно заряженный с объемной плотностью ρ, то соотношение (3.39) примет вид

где - расстояние от элемента ΔS, характе­ризуемого координатами ζ£, η, до точки N с координатами х, у, в которой вычисляется потенциал.

От формулы (3.41) нетрудно перейти к выражению для потенциала, созданного произвольным двумерным (не зависящим от z) распределением зарядов с плотностью ρ:

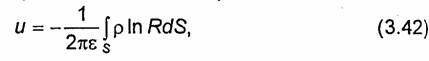
где S - площадь сечения данной системы зарядов плоскостью, перпендикулярной к оси Z (рис. 3.5).

Функцию и, определяемую соотношениями (3.39)-(3.42), при­нято называть логарифмическим потенциалом.

Если поле создается зарядами, распределенными по цили­ндрической поверхности S, образующие которой параллельны оси Z, а плотность поверхностных зарядов не зависит от переменной z, то соответствующий логарифмический потенциал

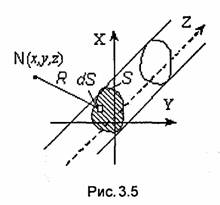
где Г-линия пересечения поверх­ности S с плоскостью, перпендику­лярной оси, Z, a R - расстояние от элемента dl до точки N, в которой вычисляется потенциал (рис. 2.9).

Из формул (3.39)-(3.43) следу­ет, что логарифмический потенциал на бесконечности нельзя принять равным нулю не только в направлении оси Z, но и в перпендикулярных к ней плоскостях. Исключение составляет случай, когда полный заряд системы равен нулю.

Поле, соответствующее потенциалам (3.42) и (3.43), убывает на бесконечности пропорционально 1/r (или быстрее), если по­верхность S (или контур Г) ограничена. Если S (или Г) не огра­ничена, то векторы Е и D на бесконечности могут иметь конечные значения (например, поле равномерно заряженной плоскости).