1.8.4. Уравнение баланса комплексной мощности

Уравнение баланса комплексной мощности может быть по­лучено либо из уравнений Максвелла в комплексной форме, либо непосредственно из теоремы Пойнтинга. Второй путь короче. При этом вывод упрощается, если в качестве исходного использовать уравнение баланса мгновенных значений мощности в форме (1.123). Перейдем от мгновенных значений мощностей, входящих в (1.123), к комплексным мощностям на основе приема, описанного в 1.8.3. Все подынтегральные выражения в (1.123) содержат про­изведения двух векторов. Заменим в этих произведениях первый вектор соответствующим ему комплексным вектором (например,

вектор Е - на Ё), а второй вектор - соответствующим ему комп­лексно-сопряженным вектором (например, j^ст-нa j^ст). Умножая обе части получающегося при этом равенства на 1/2, приходим к соотношению

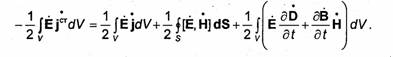
Вычисляя производные по t и учитывая обозначение (1.145), получаем уравнение баланса комплексной мощности:

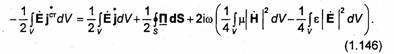
Проанализируем это уравнение. Используя формулы (1.142)—(1.144),

перепишем его в виде

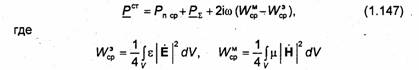
-соответственно средние за период значения энергий эле­ктрического и магнитного полей в объеме V. Из равенства ко­мплексных величин следуют отдельные равенства для их дей­ствительных и мнимых частей. Отделяя в (1.147) действительные части, получаем

Левая часть равенства (1.148) представляет собой среднюю за период мощность сторонних источников, которая равна также средней за период активной мощности сторонних источников. Второе слагаемое в правой части (1.148) равно среднему за период потоку энергии через поверхность S и соответственно среднему за период активному потоку энергии через ту же по­верхность:

Поэтому равенство (1.148) эквивалентно соотношению

Таким образом, уравнение (1.148) представляет собой урав­нение баланса средних за период мощностей. Уравнение (1.148) иногда называют также уравнением баланса активных мощностей.

Из (1.149) видно, что в тех случаях, когда поток энергии в среднем за период выходит из рассматриваемого объема в окружающее пространство. При средний поток энергии отрицателен, т.е. направлен из окружающего пространства в объем V.

Отделяя в (1.147) мнимые части, получаем

Входящие в (1.150) величины 1тР^ст и ImP_Σ; равны соот­ветственно амплитуде реактивной мощности сторонних источников и амплитуде реактивного потока энергии через поверхность S. Поэтому уравнение (1.150) иногда называют уравнением баланса реактивных мощностей.

Реактивный поток энергии изменяется со временем по гармоническому закону с удвоенной круговой частотой 2ω. В течение периода он половину времени имеет положительное значение, т.е. энергия поступает в окружающее пространство, а другую половину - отрицательное, т.е. энергия поступает из ок­ружающего пространства, в объем V. Среднее за период значение реактивного потока энергии равно нулю. Таким образом, из (1.150) следует, что разность между амплитудами реактивной мощности сторонних источников и реактивного потока энергии через огра­ничивающую этот объем поверхность S равна умноженной на 2ω разности между средними за период значениями энергий маг­нитного и электрического полей в объеме V.

Предположим, что объем V представляет собой изолиро­ванную систему (например, ограничен идеально проводящей пове­рхностью). Тогда поток комплексного вектора Пойнтинга через S будет равен нулю, и уравнения (1.149) и (1.150) примут вид

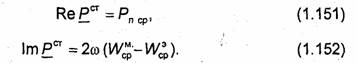
В этом случае в объеме V энергия электрического поля будет периодически преобразовываться в энергию магнитного поля и обратно. Если средние за период значения энергий электрического и магнитного полей равны, т.е.

то этот процесс протекает без участия источников, и мощность сторонних источников оказывается чисто активной (ImР^ст = 0). Ес­ли же , то периодическое преобразование энергии эле­ктрического поля в энергию магнитного поля и обратно возможно только при участии сторонних источников. При этом реактив­ная мощность сторонних источников будет отлична от нуля . Если в изолированной области мощность сторонних источников является чисто активной, то имеет место резонанс. Из изложенного следует, что для резонанса необходимо выполнение условия (1.153). Отношение

где , называют добротностью изолированной сис­темы. Выражение (1.154) можно переписать в иной форме. За­меняя со на 2π/Т, получаем

где ΔW - изменение энергии электромагнитного поля системы за период. Таким образом, добротность изолированной системы - это увеличенное в 2π раз отношение запаса энергии системы W_CP к энергии ΔW, расходуемой за период Т.

Уравнение (1.146) было выведено в предположении, что ε Отметим, что в общем случае, когда.ε уравнение баланса комплексных мощностей также имеет вид (1.147), однако при этом входящие в него величины определяются выражениями