Глава 15

ЭЛЕМЕНТНАЯ БАЗА ВОЛОКОННО-ОПТИЧЕСКИХ ЛИНИЙ СВЯЗИ (ВОЛС)

15.1. Методы реализации элементов волс

Волоконно-оптические линии связи относятся к наиболее пер­спективным средствам передачи информации. В этих линиях в ка­честве переносчика сигналов используются световые волны, пе­редатчиками чаще всего служат полупроводниковые лазеры или светодиоды, а приемниками -фотодиоды. При этом световые вол­ны, модулированные полезным сигналом, передаются по волокон­ным световодам. К основным преимуществам ВОЛС по сравнению с известными системами связи относятся: широкополосность и высокая пропускная способность, малое затухание передаваемых сигналов, высокая защищенность от внешних помех, малые габа­риты и масса [41, 42, 63]. В ВОЛС, в зависимости от их назначения, могут использоваться разные типы волоконных световодов. На­пример, в широкополосных системах дальней связи (дальность более 100 км) применяются одномодовые или градиентные волок­на, а в системах со сравнительно узкой полосой пропускания и дальностью не более 10 км используют градиентные и многомодо-вые волокна.

Подобно СВЧ тракту ВОЛС в дополнение к источнику светово­го излучения, волоконно-оптическому кабелю и фотоприемнику содержит ряд элементов, которые осуществляют требуемую обра­ботку передаваемых сигналов. Наиболее часто используют сле­дующие элементы: разъемные и неразъемные соединители, разветвители, направленные ответвители, переключатели, модулято­ры, устройства, объединяющие оптические сигналы разных частот в общем световоде (мультиплексоры) или разделяющие подобные сигналы (демультиплексоры), полосовые фильтры и др. Хотя по своим функциональным свойствам элементы оптического тракта во многом аналогичны элементам тракта СВЧ (см. гл.13-14), ис­пользование конструкций элементов тракта СВЧ в оптическом Диапазоне практически невозможно. Это связано с весьма малой величиной длины волны оптического излучения.

В оптическом диапазоне решающее значение при создании того или иного элемента имеет выбранная технология изготовления. Многие элементы и узлы изготавливаются по очень сложной технологии и почти на пределе технических возможно­стей, поскольку допуски на геометрические размеры составляют доли длины волны (доли микрометра). Сле­дует отметить, что работа по созданию элементов оптического тракта еще далека от завершения. Поэтому ряд элементов разра­ботан и освоен промышленностью, другие элементы находятся в стадии разработки. В настоящее время многие элементы могут быть реализованы в трех различных конструктивных вариантах, называемых микрооптической, интегрально-оптической или воло­конно-оптической конструкциями.

При создании устройства в микрооптическом варианте исполь­зуют методы и элементы, аналогичные применяемым в техниче­ской оптике. В технической оптике, как правило, имеют дело со световым излучением, распространяющимся в воздушной среде. Обычно электромагнитную волну, переносящую мощность свето­вого излучения, представляют в виде светового пучка, состоящего из ряда лучей. С каждым лучом связывают определенную часть энергии, переносимую волной; направление каждого луча совпа­дает с направлением перемещения световой энергии. Иногда та­кую волну называют лучевой. Как правило, некогерентный источ­ник светового излучения (светодиод) создает на своем выходе све­товой пучок, имеющий приближенно равномерное распределение амплитуд векторов поля в плоскости, перпендикулярной оси пучка. В свою очередь, световой пучок на выходе когерентного источника (лазера) имеет структуру поля, называемую распределением Га­усса, при котором амплитуда вектора Е уменьшается по опреде­ленному закону при увеличении расстояния от осу пучка (рис. 15.2). Такое излучение называют либо гауссовым пучком, либо гауссовой лучевой волной [42]; оно характеризуется величиной наибольшего сужения (талия пучка) 2и/₀ и углом расхождения в дальней зоне 2©о, которые связаны формулой где λ-длина волны излучения в среде, где происходит распространение.

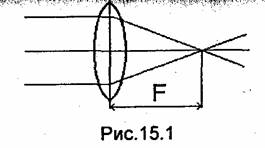
Для обработки световых пучков в технической оптике приме­няют разные элементы: линзы, призмы, зеркала, дифракционные решетки и т.д. Например, с помощью линзы пучок параллельных лучей (рис. 15.1) может быть сфокусирован (плоская электромаг­нитная волна преобразуется в сферическую), а расходящийся пу­чок может быть коллимирован, т.е. преобразован в пучок парал­лельных лучей. Подобная линза преобразует гауссов пучок с тали­ей w₁ в гауссов пучок с талией w₂ (рис.15,2). При этом расстояния

z₁ и z₂ от линзы до плоскостей с наибольшим сужением пучков оп­ределяются по формулам F-фокусное расстояние линзы,причем F>F₀, знаки перед вторыми слагаемыми либо оба положи­тельные, либо оба отрицательные. В оптических трактах, где ис­пользуются волоконные или планарные световоды, поперечные размеры световых пучков весьма малы, поэтому и элементы для их обработки должны иметь малые размеры (порядка миллимет­ра). Вследствие этого конструкция оптических устройств для ВОЛС, состоящая из ряда элементов с малыми размерами, полу­чила название микрооптическая. При изготовлении таких конст­рукций применяют достаточно сложные технологии, обеспечи­вающие необходимую точность изготовления столь малых объек­тов. Весьма не просты сборка и настройка подобных конструкций, поскольку их отдельные элементы должны быть установлены в нужном месте и должным образом ориентированы; кроме того, должна быть обеспечена необходимая жесткость и прочность всей конструкции. Сложность изготовления возрастает при увеличении числа элементов в микрооптической конструкции.

Отмеченные трудности при изготовлении микрооптических конструкций устройств удается отчасти преодолеть при ис­пользовании интегрально-оптических конструкций. В этом случае оптическое устройство или его часть, состоящие из ряда эле­ментов, соединенных отрезками линий передачи, объединяются на общей подложке и изготавливаются одновременно (подобно ин­тегральной схеме). В результате образуется миниатюрная опти­ческая конструкция, обеспечивающая весьма плотную компоновку элементов, высокую прочность и надежность, низкий уровень по­терь при передаче оптических сигналов, поскольку удается ис­пользовать минимально возможные длины соединительных отрез­ков. Как правило, интегрально-оптические конструкции элементов ВОЛС строятся на основе или планарного световода, или разных типов полосковых световодов. Планарную конструкцию должныиметь и все элементы, составляющие оптическую схему. Отсут­ствие в настоящее время полного набора таких элементов зат­рудняет интеграцию на общей подложке достаточно больших и сложных оптических схем. Кроме того, трудности в использовании интегрально-оптических конструкций в ВОЛС состоят в обеспе­чении эффективной стыковки выходов таких схем с волоконными световодами.

Наиболее удобными для использования в оптических трактах ВОЛС являются элементы, имеющие волоконно-оптическую конст­рукцию. Подобные элементы конструируются непосредственно внутри волоконного световода. В настоящее время это наименее разработанная область техники: создано весьма малое количество элементов, имеющих такую конструкцию [42].

Отметим, что, хотя для большинства используемых устройств оптического тракта существует несколько возможных вариантов конструктивной реализации, для каждого конкретного устройства существует оптимальный вариант реализации, при котором обес­печиваются лучшие параметры и технологичность.

Так как фазовая скорость, длина волны, коэффициент осла­бления и другие характеристики электромагнитной волны зависят от свойств среды, то, изменяя диэлектрическую или магнитную проницаемость среды, можно влиять на распространение волны. Это явление используется в управляющих оптических устройствах, таких как переключатели, модуляторы, регулируемые делители сигналов, фазовращатели и др. Параметры некоторых сред изме­няются при приложении к ним постоянного электрического поля (электрооптический эффект), постоянного магнитного поля (магни­тооптический эффект), или механического воздействия (пьезооптический эффект). Наиболее ярко электрооптический эффект про­является в диэлектриках и полупроводниках с кристаллической структурой. Подобная структура придает кристаллам анизотроп­ные свойства (коэффициент преломления п такой среды зависит от направления распространения световой волны). Анизотропия . бывает естественная, проявляющаяся в отсутствии внешнего по­стоянного электрического поля, и наведенная, проявляющаяся только при приложении внешнего электрического поля. В анизо­тропной среде диэлектрическая проницаемость ε_r=п² становится тензором (см.1.2.3). Если оси координат совпадают с главными осями кристалла, то его оптические свойства описываются тремя показателями преломления п_х, п_у, n_z. Влияние такого кристалла на распространение электромагнитной волны учитывают с помощью эллипсоида показателей преломления (рис. 15.3), называемого оп­тической индикатрисой и описываемого уравнением [42] (х/п_х)²+ + (y/n_y)²+(z/n_z)²=1.

Пусть волна распространяется, как показано на рис. 15.3. Плоскость, проходящая через нача­ло координат перпендикулярно вектору Пойнтинга, пересечет эллипсоид по эллипсу с полуосями п₁ и п₂. Если вектор Е волны параллелен полуоси п₂ коэффициент преломления кристалла для такой волны равен п₂. Для волны, вектор Е кото­рой параллелен полуоси п₂, коэффициент пре­ломления равен п₂. Под воздействием внешнего электрического поля изменяются ориентация в

пространстве и величина полуосей эллипсоида показателей пре­ломления. Например, кристалл LiNbO₃ является одноосным [42]. Для него п_х = n_у = п₀, a n_z = n_e; эллипсоид является симметричным относительно оптической оси Z. Приложение постоянного электри­ческого поля Е_о вдоль оси Z не изменяет ориентацию эллипсоида в пространстве, а изменяет лишь величины п₀ и п_e на величину Та­ким образом, коэффициент преломления п волны зависит от ее направления распространения, поляризации и величины внешнего электрического поля Е_о. В общем случае зависимость п от Е_о оп­ределяется формулой где r-линейный электрооптический коэффициент (коэффициент Поккельса), R-квадратичный электрооптический коэффициент (коэффициент Керра). Как правило, при конструировании управляющих опти­ческих элементов используют линейный электрооптический эф­фект, называемый эффектом Поккельса [65] и применяют мате­риалы, где этот эффект наиболее ярко выражен [42]: танталат лития LiTaОз, ниобат лития LINbO₃, арсенид галлия GaAs и др.

Как было показано в гл.14, намагниченный феррит обладает анизотропными свойствами, его магнитная проницаемость стано­вится тензором. При этом величина отдельных компонент тензора изменяется при изменении внешнего магнитного поля Н_о (магни­тооптический эффект). Наибольшее применение на практике при создании элементов ВОЛС находят ферриты типа железоиттриевого граната [41]. Использование подобного материала позво­ляет строить оптические элементы на основе эффекта Фарадея либо использовать ферромагнитный резонанс (оптические вен­тили) (см.14.3).

Акустооптический эффект заключается в изменении пока­зателя преломления вещества при деформациях, вызванных ме­ханическим воздействием, например сжатием или растяжением. Обычно для создания сжатий или разряжений в веществе воз­буждают ультразвуковые колебания (звуковые волны). Наиболее широкое применение на практике находят следующие акустооптические материалы: арсенид галлия (GaAs), плавленый кварц, германий и др [64].