14.3.2. Свойства ферритов в диапазоне свч

Магнитные свойства вещества. Ферриты.Как известно, атомы всех веществ состоят из положительно заряженного ядра и определенного числа отрицательно заряженных электронов. Каждый электрон вращается по некоторой орбите вокруг ядра, одно­временно вращаясь вокруг своей собственной оси. Поскольку электрон заряженная частица, то его перемещение по замкнутой траектории эквивалентно протеканию тока в контуре, поэтому ор­биту каждого электрона можно рассматривать как элементарную рамку с током. Под влиянием тока, протекающего по рамке, в ок­ружающем пространстве возникает постоянное магнитное поле, силовые линии которого перпендикулярны плоскости рамки. Этому магнитному полю соответствует орбитальный магнитный момент электрона М_орб. Кроме этого, при вращении электрона вокруг своей оси возникает спиновый магнитный момент М_сп.

Электрон обладает определенной массой, поэтому каждый электрон может рассматриваться в первом приближении как вол­чок (гироскоп) с массой т, вращающийся вокруг центра атома и одновременно вокруг собственной оси. Это обусловливает нали­чие у электрона двух механических моментов количества движе­ния: орбитального L_орб и спинового L_сп. Теоретические и экспе­риментальные исследования показали, что

где е и т-соответственно заряд и масса электрона. Знак минус, а значит, и антипараллельная ориентация магнитных и механи­ческих моментов обусловлены отрицательным зарядом электрона.

Полный магнитный и механический моменты атома есть гео­метрические суммы соответственно магнитных и механических спиновых и орбитальных моментов всех электронов в атоме. Маг­нитный момент ядра примерно на три порядка меньше магнитного момента электрона, поэтому влиянием магнитного момента ядра можно пренебречь.

Исследования вещества показали, что у большинства атомов наблюдается антипараллельная ориентация спиновых магнитных моментов у любых соседних двух электронов на орбите, т.е. сум­марный магнитный момент этих атомов близок к нулю. Иск­лючение составляют металлы переходных групп (группа железа, палладия, платины и др.), у которых наблюдается параллельная ориентация спиновых магнитных моментов у части электронов на 1 орбите. Например, у атома железа на предпоследней орбите на-I ходятся четыре электрона с параллельными спинами, у атома кобальта-три и т.д. В постоянном магнитном поле атомы этих металлов ведут себя подобно стрелке компаса: их магнитные моменты ориентируются параллельно приложенному полю.

Как будет видно из дальнейшего изложения, принцип действия ферритовых устройств диапазона СВЧ основан на взаи­модействии магнитного поля электромагнитной волны с нескомпенсированными магнитными моментами атомов, чтооы такое взаимодействие стало возможным, электромагнитная волна дол­жна проникать в вещество и распространяться в нем. В провод­ники электромагнитные волны почти не проникают. Эту трудность можно устранить, если использовать не ферромагнитные ме­таллы, а обладающие свойствами диэлектриков химические, сое­динения таких металлов (обычно железа) с другими элементами. Подобные магнитные диэлектрики, называемые ферритами, име­ют достаточно высокое удельное сопротивление - порядка 10⁶...10¹¹Ом/см; их относительная диэлектрическая проницаемость зависит от со­става феррита и обычно равна 5...20.

Состав простейших ферритов, являющихся твердыми раство­рами окислов металлов и Fe₂O₃, описывается следующей хими­ческой формулой: Me⁺²0-Fe₂0₃, где Ме⁺²-ион двухвалентного ме­талла, обычно это Ni, Co, Mn, Cu, Zn и др. Часто применяют так называемые смешанные ферриты, в состав которых входят одно­временно ионы двух и большего числа металлов. Ферро­магнитными свойствами обладает соединение вида Y₃Fe₂(Fe0₄)3, называемое иттриевым феррогранатом. Ферриты могут быть поли­кристаллическими и монокристаллическими. Технология производ­ства поликристаллических ферритов совпадает с технологией производства керамики: из смеси мелко измельченных окислов с пластификатором формируют необходимые образцы ферритовых изделий, которые затем обжигают при температуре 1000-1400 °С. Ферритовые монокристаллы (например, иттриевые феррогранаты) выращивают по технологии, сходной с технологией полупровод­никовых материалов.

Экспериментальные исследования показали, что в ферритах вклад орбитальных моментов в общий момент обычно мал, поэто­му магнитные свойства ферритов определяются в основном спи­новыми магнитными моментами атомов.

Прецессия магнитного момента. Предположим, что электрон с магнитным моментом М_сп и механическим моментом L_сп помещен во внешнее постоянное магнитное поле Ho=z_oHo, направление ко­торого не совпадает с М_сп, (рис. 14.48). Под влиянием внешнего по­ля магнитный момент стремится повернуться и установиться па­раллельно Н_о, причем вращательный момент Т равен {58]:

Т=[М_СП,Н₀]. (14.21)

Однако наличие механического момента L_сп делает электрон подобным гироскопу, ось которого под влиянием действующих сил процессирует (вращается). Поэтому под действием поля Н_о концы векторов L_сп и М_сп начинают прецессировать вокруг Н_о. Траектория движения концов этих векторов изображена на рис. 14.48 сплошной

линией. Скорость перемещения L_сп равна вели­чине вращательного момента T:dL_сп/dt=T= - [М_сп, Но]. Подставив в это равенство значение L_сп из (14.20), приходим к уравнению

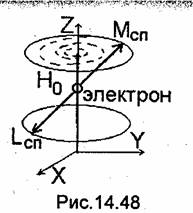
Решение уравнения (14.22), выполненное в [58], показывает, что конец вектора М_сп описывает окружность, вращаясь по часовой стрелке, если смотреть вдоль вектора Н_о (рис. 14.48). При этом кру­говая частота вращения вектора, называемая круговой частотой свободной процессии, вычисляется по формуле

В реальных ферромагнитных средах всегда имеет место по­тери. Поэтому конец вектора М_сп движется по свертывающейся спирали, как показано пунктиром на рис. 14.46. Через время по­рядка 10^-8 прецессия практически полностью прекращается, и вектор М_сп устанавливается параллельно Н_о.

При определенной величине Н_о, зависящей от состава ферритового образца, его формы и некоторых других факторов, прак­тически все нескомпенсированные магнитные моменты ориен­тируются параллельно друг другу и внешнему полю. Феррит на­магничивается до насыщения. В результате вектор магнитного момента единицы объема феррита М_о, равный произведению М_сп на число N некомпенсированных магнитных моментов в единице объема, установится параллельно Н_о:Мо=NМ_сп=z_оМ.

Вектор Н_о оказывает одинаковое влияние на все неском­пенсированные магнитные моменты. Поэтому уравнение (14.22) описывает движение не только магнитного момента отдельного электрона, но и всех магнитных моментов в единице объема, т.е. в (14.22) можно вместо М_сп подставить М_о.

Тензор магнитной проницаемости феррита. Если в намаг­ниченной под воздействием поля Н_о ферритовой среде распро­страняется электромагнитная волна с произвольно ориентиро­ванным вектором напряженности магнитного поля H = H_mcos(ωf), то на магнитные моменты действует суммарное поле с вектором

В этом случае ориентация в пространстве вектора H_s не оста­ется постоянной, ибо длина вектора Н изменяется по гармоническому закону (кроме случая Н||Но , но этот случай не пред­ставляет интереса для рассматриваемых здесь вопросов). Изме­нение ориентации вектора Н вызывает прецессию магнитных моментов. Эта прецессия уже не будет затухающей, так как от­сутствует какое-либо определенное направление внешнего поля, параллельно которому могли бы установиться магнитные мо­менты. Возникает так называемая вынужденная прецессия, час­тота которой совпадает с частотой электромагнитной волны.

Если ||Н_т | |<< Н_о, отклонения вектора Н_Σ от оси Z незначи­тельны, соответственно невелики и отклонения суммарного век­тора магнитного момента единицы объема M_Σ от оси Z. В этом