14.2.3. Реализация эквивалентных схем фильтров свч

В диапазоне СВЧ, как правило, фильтры строят из элементов с распределенными параметрами. .При этом схемы, состоящие из элементов с сосредоточенными параметрами, рассматриваются как эквивалентные схемы. Синтезировав эквивалентную схему фильтра, как было показано выше, выполняют второй этап про­ектирования - реализуют полученную эквивалентную схему. Вна­чале пытаются с помощью элементов с распределенными пара­метрами смоделировать поведение сосредоточенных элементов эквивалентной схемы. Однако такой подход к синтезу конструкции СВЧ фильтра является лишь начальным и весьма грубым при­ближением, поскольку при этом не учитывается ряд важных фак­торов, влияющих на АЧХ синтезированной конструкции: перио­дичность частотных характеристик элементов с распределенными параметрами, дисперсия в отрезках линии, влияние неоднородностей в полученной конструкции и т.д. Поэтому получаемую вначале конструкцию рассматривают как первое или начальное приближение при реализации. Затем для полученной конструкции строят уточненную эквивалентную схему, пытаясь учесть ее осо­бенности (влияние неоднородностей, дисперсию и тепловые поте­ри в отрезках линии и т.д.). Уточненная эквивалентная схема позволяет реализовать конструкцию фильтра во втором прибли­жении и т.д. На практике, как правило, при разработке конструкции фильтров СВЧ используют декомпозицию и параметрический синтез конструкции, полученной в первом приближении (см.12.6).

Фильтр нижних частот на элементах с распределенными параметрами. Наиболее просто эквивалентную схему ФНЧ (рис. 14.23) можно реализовать с помощью коротких отрезков ли­нии передачи, используя эквивалентные схемы таких отрезков, приведенные в табл. 12.1. В этом случае конструкция ФНЧ состоит из каскадного соединения коротких отрезков линии с высоким. Z_BB и низким 2_ВH волновыми сопротивлениями, включенного в разрыв линии передачи с волновым сопротивлением Z_B, т.е. в данном слу­чае R_H=R_r=Z_B. На рис.14.31 показана микрополосковая конструкция ФНЧ. Обычно при синтезе конструкции величины 2_ВВ и 2_ВН выбирают исходя из конструк­тивных особенностей линии, а требуемую величину индук­тивности или емкости элемента обеспечивают подбором длин отрезков. Отметим, что величи­на волнового сопротивления линии должна выбираться из условия

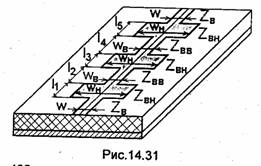
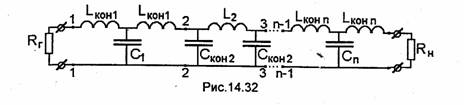
физической реализуемости линии и отсутствия в ней высших типов волн. Поэтому, выбрав величины Z_BB и Z_BH, определяют по формулам синтеза для ис­пользуемой в конструкции линии передачи (см. 10.6) величины w_B и w_H (рис.14.31). В первом приближении длины отрезков l _{1 ,}l_{2 ,…}l _n можно вычислить по формулам табл.12.2. Для определения более точных значений длин отрезков линии строим уточненную эквивалентную схему для нее (рис.14.32). Для этого каждый отрезок линии заменяем полной Т- или П-образной эквивалентной схемой (рис.12.35), величины концевых индуктивностей и емкостей L_K0H и Скон определяем из (12.56) или (12.57) соответственно. Учет влияния дополнительных элементов схемы на конструкцию ФНЧ проводят следующим образом: вначале рассчитывают уточненные значения емкостей, не учитывая концевые индуктивности, т.е. C₁ =C₁-С_конг2 ;Сз=Сз-С_кон2-С_Конз; …;С_п⁼С_п-С_конп-1,по которым рассчитывают длины нечетных отрезков, реализующие, эти емкости. Зная новые длины l _{1 ,}l_{3 ,…}l _n вычисляем с их помощью концевые индуктивности и уточненные значения индуктивностей L₂=L₂-L_KOH1 -1кон2;-;L_n-1'=L_n-₁-L_конn-Lко_{H n-1}, позволяющие наайти новые значения длин четных отрезков l _{2 ,}l_{4 ,…}l _n-1.Процесс на­хождения уточненных длин всех отрезков повторяют до тех пор, пока их значения не начнут приближаться к некоторым фикси­рованным величинам (итерационный процесс).

Уточнением эквивалентной схемы рис.14.32 конструкции ФНЧ (см.рис.14.31) является учет влияния неоднородностей, возни­кающих в местах стыка отрезков линии с высоким и низким вол­новыми сопротивлениями. На рис.14.33, а показаны неоднород­ность в микрополосковой линии, образованная скачкообразным изменением ширины полоски, и ее эквивалентная схема (рис.14.33, б), взятая из [36], где приведены также формулы для вычисления С_а и L_a. Поэтому если в схему рис.14.32 в сечениях

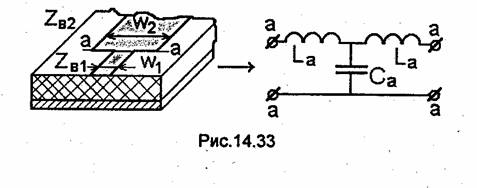
1-1,2-2, ...,п-п добавить эквивалентные схемы неоднородностей (рис.14.33), то образуется более точная эквивалентная схема, позволяющая вычислить уточненные значения индуктивностей и емкостей, а следовательно, и более точные величины длин от­резков конструкции. Аналогично синтезируется конструкция ФНЧ на основе любой полосковой или коаксиальной линии.

Полосовые фильтры на элементах с распределенными параметрами. Включаемые параллельно параллельные контуры эквивалентной схемы полосового фильтра (рис.14.26) сравните­льно просто реализуются в диапазоне СВЧ, например элементы 4 и б из табл. 12.1, выполненные на любой полосковой или коакси­альной линии; резонансная диафрагма в волноводе (см. рис. 12.38); параллельно подключенные к линии реактивные шлейфы опреде­ленной, длины (см.12.1.3); любой объемный резонатор, рабо­тающий в проходном режиме в линии передачи. Однако реали­зация последовательного контура, включенного последовательно в схему (рис.14.26), вызывает затруднения, что связано с необ­ходимостью реализации последовательно подключенной емкости. Казалось бы, что зазор в центральном проводнике коаксиальной линии или в полоске полосковой линии позволяет решить эту задачу. Однако на практике такой зазор используют крайне редко, поскольку для реализации нужных величин емкостей могут потребоваться очень малые зазоры, что создает технологические трудности при изготовлении, кроме того, более точная эквива­лентная схема зазора не последовательная емкость, а П-образная цепь, состоящая из последовательной и параллельных емкостей [36]. Обычно последовательно подключенная емкость реализуется с помощью сосредоточенного конденсатора, выполненного в виде ЧИП и изготовленного методами толстопленочной или тонко­пленочной технологии [36]. Поэтому самое простое решение при реализации последовательного контура схемы рис.14.26-это каскадное соединение отрезка линии с высоким волновым сопро­тивлением, реализующим индуктивность, с сосредоточенным кон­денсатором. Такое решение приемлемо лишь на относительно низких частотах, когда допустимо использовать элементы с сосре­доточенными лишь параллельные контуры, включенные параллельно.

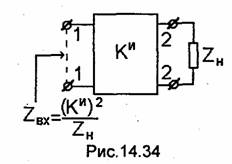
Идеальный инвертор сопротивления (рис.14.34)-это четырехполюс­ник, характеризуемый коэффициентом ин­версии К^и. Инвертор имеет следующие свойства: при подключении к его выходу сопротивления Z_H его входное сопротивление Z_BX= (K^и)²/Zh, а фазовый сдвиг, получаемый волной напря­жения, проходящей с его входа на выход, равен nπ/2, где n- целое нечетное число. Благодаря свойствам инвертора последова­тельный контур, включенный в линию последовательно, имеет та­кое же входное сопротивление, что и параллельный контур, вклю­ченный параллельно с инверторами на каждой стороне. На этом основании эквивалентная схема полосового фильтра с исполь­зованием инверторов имеет вид, показанный на рис. 14.35. Пос­кольку при неизменном Z_H (рис.14.34) величина Z_BX инвертора за­висит от К, то в эквивалентной схеме рис.14.35 по сравнению со схемой рис.14.26 имеются дополнительные степени свободы при реализации - коэффициенты инверсии инверторов. При этом, что­бы АЧХ схемы (рис.14.35) и схемы (рис.14.26) были бы идентичны, должны выполняться соотношения [35]

В сравнительно узкой полосе частот свойствами, близкими к свойствам идеального инвертора, обладает четвертьволновый от­резок линии передачи, волновое сопротивление которого играет роль коэффициента инверсии (12.29). Такие отрезки и применяют при реализации узкополосных полосовых фильтров, имеющих эк­вивалентную схему рис.14.35. Подобные конструкции называют фильтрами с четвертьволновыми связями между резонато­рами. На рис. 14.36 показана микрополосковая конструкция двухзвенного полосового фильтра, реализующая схему рис.14.35. В качестве инверторов исполь­зованы четвертьволновые отрезки МПЛ, волновые соп­ротивления которых вычи­сляются по (14.17) в пред­положении, что все контуры состоят из элементов с оди­наковыми параметрами. Кон­туры реализуются с по­мощью реактивных шлейфов

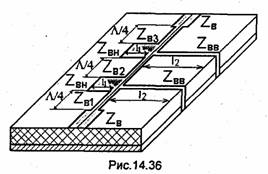
(элемент 4 в табл.12.1). Конст­рукцию (рис. 14.36) можно моди­фицировать, подключив к концу отрезков длиной l₂ вместо ко­роткого замыкания разомкнутый на конце четвертьволновый от­резок. При этом появляется до­полнительное преимущество: через фильтр можно подавать постоянное напряжение смеще­ния в случае, если к его выходу подключено полупроводниковое устройство.

На рис. 14.37 показана трехзвенная конструкция полосового фильтра на основе прямоугольного волновода, соответствующая эквивалентной схеме (рис.14.35). Фильтр выполнен в виде отрезка волновода, в котором на определенных расстояниях друг от друга впаиваются решетки из индуктивных стержней, образующие про­ходные объемные резонаторы с колебанием H₁₀₁, реализующие контуры эквивалентной схемы. Количеством индуктивных стерж­ней и их диаметром обеспечивают требуемую нагруженную доб­ротность каждого резонатора (14.16). Поскольку фаза проходящей через неоднородность волны (в данном случае через решетку стержней) зависит от величины проводимости неоднородности, то длина каждого резонатора l_1, l_{2 ,} l ₃ будет несколько отличаться от Λ/2, и ее можно определить, зная проводимость каждой решетки. По той же причине и расстояния между резонаторами l₁₂ и l₂з бу­дут несколько отличаться от Л/4. Необходимые для расчета фор­мулы можно найти в [33]. Из-за неизбежных при изготовлении кон­струкции погрешностей резонансные частоты резонаторов в фильтре могут отличаться от требуемой. Для устранения этого в каждый резонатор вводится настроечный емкостной стержень, ввинчиваемый через широкую стенку волновода (рис. 14.37).

Отметим, что емкость, включенная в линию последовательно также обладает свойствами инвертора сопротивлений [35]. Поэто­му при реализации эквивалентной схемы (рис.14.35) на полосковых или коаксиальной линии в качестве проходного резонатора используют полуволновый отрезок линии (элемент б в табл. 12.1 в гл.12), а в качестве инвертора - зазор в центральном проводнике линии, эквивалентной схемой которого в первом приближении и является последовательная емкость. На рис. 14.38 показана конст­рукция двухзвенного коаксиального полосового фильтра. Требуе­мые величины коэффициента инверсии обеспечиваются подбором

величины зазоров s_1, s₂ и s₃. При этом длина каждого резонатора l₁ и l₂ будет несколько отличаться от Л/2 из-за влияния проводимостей зазоров. Необходимые формулы для расчета таких фильтров (в литературе они известны как фильтры с непос­редственными связями между резонаторами) можно найти в [35]. В конструкции (рис.14.38), использующей торцевую связь между ре­зонаторами, весьма сложно получить широкие полосы пропус­кания, поскольку для этого необходима сильная связь между резо­наторами (низкая нагруженная добротность резонаторов), а это требует изготовления очень малых зазоров между проводниками. Поэтому обычно для получения сильной связи между резонатора­ми фильтра используют боковую связь между проводниками линии (см.10.6). На рис.14.39 показана конструкция трехзвенного микро-полоскового полосового фильтра с боковой связью между резона­торами. В качестве контуров использованы объемные резонаторы, образованные полуволновыми отрезками линии, разомкнутыми с обеих сторон (см.рис. 11.15). Длины всех резонаторов равны Λ/2, a области связи с подводящими линиями и между резонаторами равны Λ/4. Сделав емкости всех контуров схемы (рис. 14.35) одина­ковыми и определив величину емкости контура по (12.57) для вы­бранного объемного резонатора, можно из (14.17) найти коэффи­циенты инверсии

Волновые сопротивления для четной и нечетной волн в связанных линиях для каждой области ^^связи можно вычислить по формулам [35]:

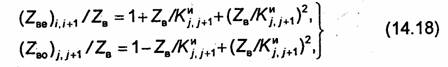
Зная Z_Be и Z_bo, по формулам синтеза связанных линии рм.10.6) определяем геометрические размеры w и s для каждой области связи.

Отметим, что в конструкции полосового фильтра (рис.14.39) можно использовать резонаторы в виде полуволнового отрезка линии, замкнутого с двух сторон. Для уменьшения габаритов кон­струкции (рис.14.39) в качестве объемных резонаторов исполь­зуют четвертьволновые отрезки линии, которые на одном конце разомкнуты, а на другом-замкнуты. При этом образуется весьма малогабаритная конструкция полосового фильтра. На рис. 14.40 показана микрополосковая пятизвенная конструкция полосового фильтра. Подобные фильтры называют в литературе фильтрами на встречных стержнях. Элементы короткого замыкания конст­рукции (рис. 14.40) можно использовать для крепления провод­ников при реализации фильтра на линиях с воздушным запол­нением (например, симметричная или несимметричная полосковые линии). Применение линий с воздушным заполнением поз­воляет уменьшить тепловые потери в полосе пропускания фи­льтра. Как правило, уровень тепловых потерь в полосе пропус­кания фильтра определяет максимальное количество звеньев в схеме фильтра, которое может реализовать та или иная конст­рукция. Методика проектирования фильтров на встречных стерж­нях (рис. 14.40) с помощью фильтра-прототипа изложена в [35].

Отметим, что при использовании объемных резонаторов, об­разованных отрезками линии, разомкнутой на концах (см. рис.11.15), длины отрезков следует выбирать несколько меньше половины длины волны: l=Λ/2-2∆ l. Это связано с концентрацией электри­ческого поля на концах резонатора, что эквивалентно подклю­чению к отрезку эквивалентной линии краевых емкостей. Величину укорочения 2 ∆ l можно рассчитать по следующим приближенным формулам [30]:

для микрополосковой линии

для симметричной полосковой линии 2∆ l ≈О.ЗЗb.

С вопросами проектирования фильтров верхних частот или режекгорных фильтров можно ознакомиться в [35].