Глава 14

ПАССИВНЫЕ УСТРОЙСТВА СВЧ

14.1. Направленные ответвители и мостовые схемы свч

14.1.1. Направленные ответвители на связанных линиях передачи

Направленным ответвителем в технике СВЧ называют че-тырехплечное устройство, или восьмиполюсник (рис.14.1), обла­дающий следующим свойством: при подаче мощности в любое плечо (например, в плечо 1) она не поступает в одно из выходных плеч (плечо 3) и делится между двумя другими плечами (плечи 2 и 4). Коэффициент деления мощности между выходными плечами зависит от конструкции ответвителя. Как правило, такие устройст­ва строятся на основе двух близко расположенных отрезков линий передачи, связанных между собой с помощью тех или иных эле­ментов связи (см.13.2). При этом мощность бегущей волны, рас­пространяющаяся по одной из линий (например, по первой), час­тично ответвляется в другую линию и поступает в одно из ее плеч. Если направление распространения волны в первой линии изме­нить на противоположное, то ответвленная мощность поступит в другое плечо второй линии, т.е. имеет место направленное от­ветвление передаваемой мощности.

Если мощность на входе плеча 1 равна P₁, а на выходах ос­тальных плеч - соответственно Р₂, Рз и Р₄, то основными парамет­рами, характеризующими работу ответвителя, являются: коэффи-

характеризующий согласование на­правленного ответвителя с подводя­щей линией при условии, что к ос­тальным плечам подключены согла­сованные нагрузки, а также диапазон частот, в пределах которого сохраня­ются требуемые значения К, D, N_p и

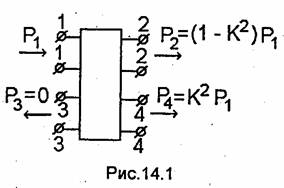
КСВ. В идеальном случае ответвитель полностью согласован с подводящими линиями, не вносит потерь в передаваемые сигна­лы, а мощности на его выходах (см. рис.14.1) зависят от коэффи­циента связи: P₂ = P₁(1-K²), Р₃ = 0, P₄ ⁼ K²P₁. Такой ответвитель описывается матрицей рассеяния [S] (см. §12.3) при N=4, в которой нужно считать S₁₁ = S₂₂ = S₃₃ = S₄₄ = 0, S₁₃= S₃₁ = S₂₄= S₄₂ = 0, |S₁₂| = |S₂₁l = |S₃₄| = |S₄₃| = √1-K², |S₄₁| = |S₁₄| = |S₃₂| = |S₂₃| = K. Аргументы отличных от нуля элементов матрицы рассеяния зави­сят от конструкции направленного ответвителя и от положения плоскостей отсчета фаз в его плечах.

Перейдем к описанию конкретных типов направленных ответвителей. Рассмотрим направленный ответвитель, образованный двумя прямоугольными волноводами с общей боковой стенкой (рис.14.2), работающими в одноволновом режиме. Пусть по пер­вому (основному) волноводу из плеча 1 в плечо 2 распространяет­ся волна Н₁₀. Эта волна через одно отверстие связи в общей узкой стенке создает во втором (связанном) волноводе две волны H₁₀, одна из которых поступает в плечо 3, а вторая - в плечо 4. Чтобы ответвленная часть мощности в связанном волноводе поступала в одно выходное плечо, в общей узкой стенке волноводов прореза­ют два одинаковых отверстия связи на расстоянии l =Λ/4, где Λ-длина волны Н₁₀ на расчетной частоте. При этом к каждому из плеч 3\л 4 будут приходить две волны Н₁₀, возбужденные первым и вторым отверстиями связи (рис.14.3). В плече 4 эти волны склады­ваются синфазно (волны проходят одинаковые пути). В плечо 3 волны, возбужденные первым и вторым отверстиями, приходят в противофазе (в этом случае путь через первое отверстие на Λ/2 короче, чем через второе) и гасят друг друга. Поэтому ответвлен­ная часть мощности из основного волновода поступает в плечо 4, а неответвленная - в плечо 2. На расчетной частоте мощность в плечо 3 не поступает. Если на расчетной частоте в основном вол­новоде волна Н₁₀ распространяется из плеча 2 в плечо 1, то от­ветвленная часть мощности в связанном волноводе поступит в плечо 3 и не поступит в плечо 4.

Коэффициент связи К двухдырочного направленного ответви­теля (рис.14.2) зависит от размеров и формы отверстий, и его

можно определить, используя результаты расчета переходного затухания одиночного отверстия в общей стенке волноводов, при­веденные в [33]. Как показывают вычисления, в двухдырочном ответвителе затруднительно получитъ K_[д_Б]>-5...-8 дБ, что связано с физическими ограничениями на максимальную величину отвер­стий, прорезаемых в общей стенке волноводов. Кроме того, откло­нение рабочей частоты от расчетного значения приводит к умень­шению величин D и N_р ответвителя, поскольку в плече 3 связанно­го волновода ответвленные волны уже не будут полностью гасить друг друга. Для расширения рабочей полосы частот и увеличения реализуемых значений К применяют многодырочные волноводные направленные ответвители, для чего в общей узкой стенке двух прямоугольных волноводов (см. рис.14.2) прорезают п отверстий связи, отстоящих друг от друга на расстоянии l, равном или мень­шем Λ/4. При этом в плече 4 связанного волновода образуется п синфазных волн, а в плече 3-такое же число волн, имеющих оп­ределенный сдвиг по фазе. Вследствие этого мощность суммар­ной волны в плече 4 будет больше, чем в плече 3 связанного вол­новода. Подбирая размеры отверстий и их количество, удается получить практически любое допустимое значение К (даже К _[д_Б]= 0, что соответствует полной связи между волноводами P₄=P₁) и тре­буемые направленность D и развязку N_р в широком диапазоне час­тот. С вопросами проектирования волноводных многодырочных ответвителей можно ознакомиться в [33].

Рассмотрим волноводный многодырочный ответвитель (рис. 14.4), в котором используются связанные через отверстия от­резки волноводов с разной формой поперечного сечения (прямо­угольный и круглый). Предположим, что диаметр круглого волно­вода настолько велик, что в нем возможно распространение не­скольких типов волн (например, Н₁₁, E₀₁. H₂₁, H_O1), причем у одной из этих волн коэффициент фазы равен коэффициенту фазы волны Н₁₀ в прямоугольном волноводе. Прямоугольный волновод рабо­тает в одноволновом режиме. При распространении волны Н₁₀ по прямоугольному волноводу от плеча 1 к плечу 2 каждое отверстие будет возбуждать в круглом волноводе волны разных типов. Однако, в плече 4 синфазно сложатся лишь волны того типа, у которого коэффици­ент фазы совпадает с коэффициентом фазы волны Н₁₀ в прямоугольном вол­новоде. Поэтому ответвленная мощ­ность в круглом волноводе будет пере­носиться преимущественно одним типом волны. Это свойство широко использу­ется для возбуждения какого-либо выс­шего типа в связанном волноводе, например для возбуждения в круглом волно­воде волны Н₀₁. При обеспечении полной связи между волноводами (К_[д_Б]) = 0) образу­ется трансформатор волны Н₁₀ прямо­угольного волновода в волну Н₀₁ крутого волновода.

При конструировании направленных ответвителей на основе коаксиальных, двухпроводных или полосковых линий передачи, работающих на TЕМ-волнах или квази-ТЕМ, применяют отрезки связанных линий (см. 10.6). В этом случае для связи двух линий передачи используется распределенная электромагнитная связь, возникающая в линиях передачи открытого типа между близко расположенными параллельными проводниками. На рис.10.47,а и б были показаны поперечные сечения связанных симметричных полосковых линий и связанных микрополосковых линий с боковой связью полосок; на рис.14.5 приведено поперечное сечение свя­занных симметричных полосковых линий с лицевой связью поло­сок. Конструкция направленного ответвителя на основе связанных микрополосковых линий с боковой связью полосок показана на рис. 14.6. Она состоит из отрезка связанных линий длиной l, имею­щего ширину полосок w и расстояние s между ними. К каждому вы­ходу отрезка связанных линий подключены подводящие линии, имеющие волновое сопротивление Z_B. Для устранения связи меж­ду подводящими линиями использован уголковый поворот на 90° в месте соединения подводящих линий с отрезком связанных линий. Аналогично строятся конструкции направленных ответвителей на основе связанных полосковых линий других типов.

Если в основной линии ответвителя (рис. 14.6) от плеча 1 к плечу 2 распространяется волна, переносящая мощность Р₁ то в связанной линии за счет распределенной электромагнитной связи в отрезке связанных линий также появится волна, переносящая ответвленную мощность Р₃=К²Р₁ в направлении плеча 3; при этом в плечо 4 ответвленная мощность не поступает: Р₄ = 0. В отличие от ранее рассмотренных волноводных направленных ответвите­лей, в направленных ответвителях на основе связанных линий передачи, работающих на ТЕМ-волнах или квази-ТЕМ, ответв­ленная часть мощности в свя­занной линии распространяется в противоположном направле­нии по отношению к направлению распространения мощности в основной линии. В настоящее время нет простого физического объяснения этого явления, строгое

математическое решение для этого случая можно найти в [1]. Поэтому в идеальном случае при обеспечении согласования с под­водящими линиями мощность Р, из плеча 1 делится между плеча­ми 2 и 3, в плечо 4 мощность не поступает. Как показывает анализ [40], величина коэффициента свя­зи К ответвителя (рис. 14.6) зависит как от параметров заполняю­щего диэлектрика, от величин w и s, так и от длины l отрезка свя­занных линий. На рис.14.7 показана зависимость величины К от электрической длины отрезка связанных линий l/Λ. Наибольший коэффициент связи обеспечивается при l=0,25Λ; 0.75Λ и т.д. При l=0,5Λ; 1,0Λ и т.д. К=0, т.е. мощность при этом полностью передается из плеча 1 в плечо 2, не ответвляясь в связанную ли­нию. Обычно длину области связи l выбирают равной 0,25Λ₀, где Λо-длина волны в отрезке связанных линий на расчетной частоте f₀. Этим обеспечивается как наибольшая величина К при фиксиро­ванных w и s, так и минимальные геометрические размеры ответ­вителя. При l=0,25Λ₀ величина К для ответвителя вычисляется по следующей формуле [40]:

позволяющие по заданным К и Z_B определить Z_Be и Z_B0 для отрезка связанных линий, а по ним, используя формулы из 10.6, рас­считать геометрические размеры w и s, т.е. синтезировать кон­струкцию ответвителя.

В рассматриваемом ответвителе сдвиг по фазе между век­торами Е волн на выходах 2 и 3 плеч составляет 90° [40], в связи с этим подобные ответвители иногда называют квадратурными. Отметим, что указанный фазовый сдвиг и идеальная направлен­ность сохраняются на любой частоте при условии, что Z_B, Z_Be и Z_B0 не зависят от частоты. При изменении частоты меняется ве­личина коэффициента связи К ответвителя (рис.14.7), что и опре­деляет его рабочий диапазон.

Отметим некоторые особенности конструирования направ­ленных ответвителей на связанных МПЛ (рис.14.6). В этом случае формулы (14.1)—(14.3) выполняются приближенно, и рассчитанный с их помощью ответвитель, как правило, требует эксперимен­тальной доработки. Однако и после этого, обеспечив требуемый коэффициент связи на расчетной частоте, не удается получить направленность более 12...14 дБ. Кроме того, как показывают экс­перименты, рабочий диапазон ответвителя на связанных микрополосковых линиях получается значительно уже, чем в ответвителях на связанных полосковых линиях с TEМ-волнами. Эти не­гативные явления обусловлены неоднородным диэлектрическим заполнением связанных микрополосковых линий, в связи с чем основными волнами в таких линиях являются четная и нечетная квази ТЕМ-волны, распространяющиеся с разными фазовыми ско­ростями (см.10.6). Это приводит к изменению величины К, а также к появлению ответвленного сигнала не только в плече 3,, но и в плече 4 связанной линии, что уменьшает направленность от­ветвителя. Обычно влияние неоднородного диэлектрического за­полнения на величину К учитывают путем изменения длины об­ласти связи, выбирая l=0,25Λ₀, где Λ_0≈(Λео⁺Λ₀о)/2, Λ_е0=Vф_е/f₀ и Λ₀о ⁼ Vфо/f₀ .Для увеличения направленности и расширения рабо­чего диапазона частот конструкцию микрополоскового ответвителя несколько изменяют, пытаясь уменьшить разницу между фазо­выми скоростями основных волн в связанных МПЛ. С основными конструкциями подобных микрополосковых ответвителей можно ознакомиться в [40]. Наиболее удачной и широко используемой на практике является конструкция (рис.14.8), известная в литературе как ответвитель Ланге. В этом ответвителе используется нес­колько связанных проводников, образующих встречно-штыревую структуру. С помощью металлических перемычек некоторые про­водники соединены между собой. Благодаря такой конструкции Ланге удалось обеспечить Vф_е≈V_ф0 и компенсировать их дисперсию в широкой полосе частот: практиче­ски в октавной полосе частот со­храняются постоянство величины К, хорошее согласование и на­правленность не хуже 24 дБ [30]. Приближенные формулы для син­теза ответвителя Ланге приведе­ны в [30].

В описанных выша полосковых конструкциях ответвителей весьма сложно обеспечить сильную связь, что связано с труд­ностями технологического характеранеобходимо изготовить про­водники с весьма малыми зазорами между ними. Кроме того, на­личие малых зазоров между проводниками снижает электри­ческую прочность ответвителя. Обычно максимально достижимый коэффициент связи в связанных линиях с боковой связью полосок не превышает -3 дБ. Правда, ответвитель Ланге выгодно отли­чается от конструкции, показанной на рис. 14.6, обеспечивая боль­шую величину зазоров между связанными проводниками при оди­наковом К. Поэтому при конструировании направленных ответвителей с сильной связью (К[д_Б] >-3 дБ) используют связанные полосковые линии с лицевой связью полосок (рис.14.5).

Существует иной тип полоскового ответвителя, позволяющий получить сильную связь и имеющий электрическую прочность, ма­ло отличающуюся от прочности подводящих линий. Это шлейфный направленный ответвитель, который весьма прост в изго­товлении на основе МПЛ или СПЛ. С небольшими изменениями его можно реализовать в коаксиальном и волноводном испол­нении. На рис. 14.9 показана микрополосковая конструкция ответ­вителя с двумя соединительными шлейфами, имеющими волно­вое сопротивление Z_вшл. Длина каждого шлейфа равна Λ₀/4, где Λ_о-длина волны в МПЛ, образующей шлейф, на расчетной часто­те f₀. Принцип действия такого ответвителя похож на принцип дей­ствия волноводного двухдырочного ответвителя (рис. 14.2). Для ответвления части мощности из основной линии, имеющей входы 1 и 2 (рис.14.9), в связанную, имеющую входы 3 и 4, используются два четвертьволновых шлейфа, включенные на расстоянии Λ₀/4 друг от друга. При распространении по основной линии волны от входа 1 к выходу 2 часть ее мощности будет проходить на выход 2, часть отражаться обратно в плечо 1, а часть через шлейфы от­ветвляться в связанную линию. Каждый шлейф возбуждает в свя­занной линии по две волны с равными амплитудами и фазами, бе­гущие в направлении плеч 3 и 4. Поэтому на выходах 3 и 4 появ­ляются по две волны, причем фазы векторов Е этих волн на расчетной частоте f₀ на выходе 3 совпадают, а на выходе 4 отли­чаются на я, ответвленная через шлейфы мощность из основной линии будет поступать на выход 3 и не поступит на выход 4. При этом нетрудно заметить, что фаза вектора Е волны на выхо­де плеча 3 отстает на π/2 от фа­зы вектора Е на выходе плеча 2. В полосковом тройнике (рис.13.24), идеальное согласование входа

с выходными плечами, а также деление выходными плечами в требуемом отношении можно обеспечить с помощью соответствующего выбора волновых сопротивлений ли­ний

в выходных плечах (см. 13.4.2). В шлейфном ответвителе ис­пользуются четыре Т-тройника, поэтому для обеспечения согласо­вания и требуемого коэффициента связи К ответвителя соответст­вующим образом подбирают величины Z_вшл и Z_B1. Анализ, выполненный в [27], показывает, что на расчетной частоте f₀ в шлейфном ответвителе обеспечивается заданная величина К, максимальная направленность и согласование с подводящими ли­ниями, имеющими волновое сопротивление Z_B, при Z_B1 = √1-K² Z_B и Например, при равном делении входной мощности между выходными плечами 2 и 3 (К= 0,707 или К[_ДБ] =

Отметим, что приведенные фор­мулы получены в пренебрежении реактивными сопротивлениями в эквивалентной схеме Т-тройников. При конструировании полосковых шлейфных ответвителей с сильной связью (К→1 или К[_ДБ] →0дБ) возникают определенные трудности, поскольку при сильной связи величины Z_B1 и Z_ВШЛ оказываются малыми, что при­водит к недопустимо большой ширине полосок. Напомним, что максимальная ширина полоски МПЛ ограничивается тем значени­ем, при котором в линии возникают высшие типы волн в заданном диапазоне частот (в данном случае-в рабочем диапазоне ответ­вителя). Поэтому для обеспечения сильной связи используют или большее число соединительных шлейфов (например, три) в конст­рукции [40], или применяют каскадное соединение нескольких двухшлейфных ответвителей, каждый из которых имеет физически реализуемый коэффициент связи [30].