12.5. Построение эквивалентных схем простейших цепей свч. Реализация цепей из сосредоточенных элементов в диапазоне свч

Применение метода декомпозиции для анализа сложной цепи СВЧ требует знания или характеристических матриц, или эквива­лентных схем базовых элементов цепи. Кроме того, на практике решается и обратная задача: по заданным функциональным свой­ствам проектируемого устройства вначале выбирают его эквивале­нтную схему, состоящую из сосредоточенных элементов L, С, R и отрезков эквивалентной линии; затем на основе этой схемы строят конструкцию устройства, пытаясь реализовать сосредоточенные элементы с помощью элементов с распределенными параметрами.

Это вызвано тем, что физические размеры сосредоточенных элементов L, С и R с повышением частоты уменьшаются и на час­тотах выше нескольких сотен мегагерц становятся настолько ма­лыми, что их изготовление вызывает серьезные трудности. Кроме того, с повышением частоты на параметры сосредоточенных эле­ментов все большее влияние оказывают тепловые потери в них и потери на излучение. Поэтому, как правило, в диапазоне СВЧ вме­сто подобных элементов используют элементы с распреде­ленными параметрами, например отрезки линий передачи. Под­бором длины и волнового сопротивления отрезков линии стара­ются смоделировать поведение сосредоточенных элементов в со­ответствующей эквивалентной схеме устройства.

Характеристические матрицы базовых элементов определяют или из решения электродинамической задачи, или эксперимен­тально. На основе найденной матрицы строят эквивалентную схе­му элемента. Например, если для взаимного четырехполюсника (рис.12.34) известна матрица || Z || или || У||, то с ним обычно со­поставляют либо Т-образную {рис.12.34) либо П-образную (рис. 12.34) эквивалентные схемы; величины элементов эквива­лентной схемы находят, приравнивая матрицы сопротивлений (для Т-схемы) или матрицы проводимостей (для П-схемы) на требуемой частоте [30]:

для Т-схемы

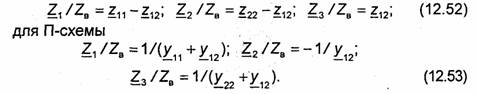
Рассмотрим эквивалентные схемы некоторых базовых элементов.

Эквивалентная схема однородного отрезка линии пере­дачи. Такой отрезок может быть представлен четырехполюс­ником, и его эквивалентная схема выбирается или в виде Т-, или в виде П-схемы (рис.12.34). Величины элементов этих схем можно найти по (12.52) и (12.53), предварительно вычислив эле­менты матриц || Z || и || Y || по (12.48)-(12.48) по известной матрице || S || (рис.12.30):

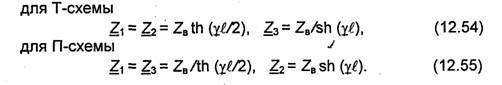
Если длина отрезка l мала, можно пренебречь тепловыми по­терями в нем (α = 0 и γ.= iβ), при этом гиперболические функции в (12.54) и (12.55) перейдут в тригонометрические, эквивалентная схема отрезка будет состоять лишь из реактивных элементов (рис.12.35):

Формулы (12.56) и (12.57) позволяют связать параметры со­средоточенных элементов и элементов с распределенными пара­метрами. Например, для коротких отрезков линии (l<<Λ), учиты­вая, что при малых х можно считать tgx≈sinx≈x, получаем Поэтому, если в разрыв линии с волновым сопротивлением Z_B включить короткий отрезок с намного большим волновым сопротивлением Z_B1, то эквивалентной схемой такой це­пи будет индуктивность, последовательно включенная в разрыв эквивалентной линии (при большой величине Z_B1 из (12.56)-(12.57) следует, что X>>B, т.е. С→0, (рис.12.35)). Аналогично можно по­казать, что если в разрыв линии включить отрезок с намного меньшим волновым сопротивлением, чем у линии, то эквивалент­ной схемой такой цепи будет емкость, параллельно подключаемая в эквивалентную линию. В табл.12.1 приведены некоторые базо­вые элементы цепей СВЧ, состоящие из отрезков полосковых линий передачи (на рисунках в таблице изображены конструкции

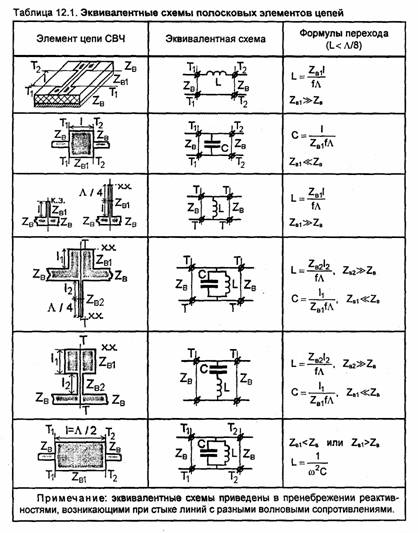
полоски для СПЛ или МПЛ), соответствующие им эквивалентные схемы и формулы перехода. По данным таблицы несложно изо­бразить конструкцию соответствующих элементов на основе коак­сиальной или двухпроводной линии передачи.

Эквивалентные схемы отражающих неоднородностей в волноводных трактах. В таких трактах для реализации сосредо­точенных элементов эквивалентных схем в волновод вводят спе­циальные отражающие неоднородности.

Волноводные диафрагмы. Диафрагмой называют тонкую металлическую пластину, расположенную в поперечной плоскости волновода и частично перекрывающую его поперечное сечение. На рис. 12.36 показана диафрагма, уменьшающая лишь размер широкой стенки прямоугольного волновода. Считаем толщину диафрагмы пренебрежимо малой и не учитываем тепловые потери в ней. Волновод работает в одноволновом режиме. При пост­роении эквивалентной схемы будем руководствоваться следую­щими физическими соображениями: свойства элемента, обладаю­щего способностью концентрировать вблизи себя энергию элект­рического поля W_зл, близки к свойствам конденсатора, вследствие этого такой элемент можно эквивалентно представить в виде реак­тивности емкостного характера; если же элемент концентрирует вблизи себя энергию магнитного поля W_Maг, то его можно эквива­лентно представить в виде реактивности индуктивного характера, а если вблизи элемента концентрируется и та и другая энергия, то при W_эл>W_маг элемент можно эквивалентно представить в виде реактивности емкостного характера, а при W_эл<W_маг-индуктивного

характера.

Рассмотрим диафрагму, изображенную на рис. 12.36. При взаимодействии распространяющейся по волноводу волны Н₁₀ с диафрагмой вблизи последней возникает структура магнитного поля, показанная на рис.12.36, т.е. в данном случае поперечные и продольные токи, текущие по широким стенкам волновода, час­тично замыкаются через пластины диафрагмы, с ними связано до­полнительное магнитное поле, возникающее вблизи диафрагмы. Это приводит к увеличению концентрации энергии магнитного поля в области диафрагмы. Поэтому эквивалентной схемой рассмат­риваемой диафрагмы является индуктивность, подключаемая параллельно в эквивалентную линию (см. рис.12.36). Для тонкой диафрагмы можно считать расстояние между полюсами 1-1 и 2-2 равным нулю. Формулы для расчета величины X_L по заданным размерам диафрагмы d₁ и d₂ можно найти в [33]. Рас­сматриваемая диафрагма (рис.12.36) получила наз­вание индуктивная диа­фрагма.

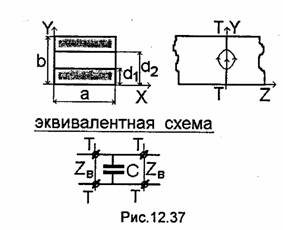
Диафрагма, изображенная на рис. 12.37, частично уменьшающая лишь размер узкой стенки прямо­угольного волновода, называется емкостной диафрагмой. При рас­пространении волны Н₁₀ по волно­воду между кромками диафрагмы концентрируются силовые линии электрического поля, что приводит к увеличению концентрации энергии электрического поля в области диафрагмы. Поэтому эквивалентной схемой рассматриваемой диа­фрагмы является емкость, подключаемая параллельно в эквива­лентную линию. Расчетные формулы для этого случая можно най­ти в [33].

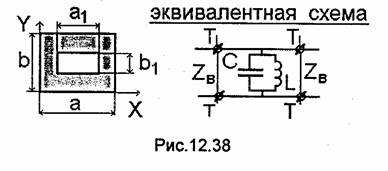
Диафрагма, образованная совмещением в одной плоскости волновода индуктивной и емкостной диафрагм, называется резо­нансной диафрагмой (рис.12.38). Размеры отверстия а₁ и b₁ могут быть выбраны так, чтобы на заданной частоте коэффициент отра­жения волны Н₁₀ от диафрагмы был бы равен нулю [33] (это озна­чает, что в эквивалентном контуре возникает резонанс, т.е. W_эл=W_маг в области диафрагмы).

Реактивный стержень в прямоугольном волноводе -это металлический проводник, установленный параллельно вектору Е волны Н₁₀ и соединенный по крайней мере с одной стороны с ши­рокой стенкой волновода (рис. 12.39). Иногда его называют реак­тивным штырем. Отметим, что аналогичные стержни (штыри) ус­танавливаются и в других линиях передачи. Эквивалентной схемой тонкого (d<<a) реактивного стержня является последовательный контур, включенный в эквивалентную линию параллельно. Индук­тивность связана с токами проводимости, протекающими по стержню, а емкость-с концентрацией электрического поля в зазо­ре между торцом стержня и стенкой волновода. Формулы для рас­чета X_L и Х_с можно найти в [33]. Анализ стержня в волноводе, вы­полненный в [38], показывает, что при длине стержня l≈λ/4 вели­чины X_L≈X_C, при этом сопротивление контура стремится к нулю

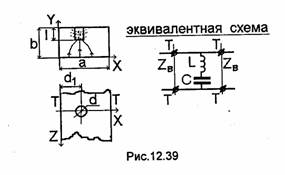
(резонанс), из-за чего вся энергия, переносимая падающей волной в волноводе, полностью отражается от стержня. На практике из-за конечной проводимости металла, модуль коэффициента отраже­ния от стержня несколько меньше единицы. При l<λ/4 реактивное сопротивление контура становится емкостным, а при l>λ/4 - ин­дуктивным.

В настоящее время существует большое число научных работ, посвященных построению эквивалентных схем как для раз­ных неоднородностей в линиях передачи, так и для простейших конструкций элементов тракта СВЧ. Расчетные формулы и экви­валентные схемы для волноводных и коаксиальных элементов можно найти в [33,39]; сведения для полосковых элементов в [36, 40]; данные для элементов оптических трактов в [41,42]. При ис­пользовании тех или иных справочных данных особое внимание следует обращать на границы применимости и обеспечиваемую точность.