12.4. Метод декомпозиции и матричное описание сложных цепей свч

При анализе произвольной цепи СВЧ необходимо определить элементы ее матрицы рассеяния на любой частоте из требуемого диапазона, что позволяет найти электрические характеристики цепи. Элементы матрицы ||S|| находятся или из решения соответствующей электродинамической задачи или измеряются экспе­риментально. Предпочтение следует отдать первому, так как в этом случае объем и качество получаемой об объекте ин­формации существенно выше, если решение задачи проведено с достаточной точностью. Однако нахождение решений уравнения Максвелла для сложных цепей СВЧ, когда граничные условия за­даются на поверхностях сложной конфигурации, даже при исполь­зовании ЭВМ встречает серьезные трудности, связанные главным образом с огромным объемом вычислений. Как правило, необхо­димые решения удается получить для ограниченного числа доста­точно простых элементов цепи СВЧ (индуктивные и емкостные диаграммы, реактивные штыри, несложные разветвления и т.д.). Поэтому одним из наиболее широко применяемых на практике ме­тодов расчета электрических характеристик сложных СВЧ цепей является декомпозиция (расчленение) сложного устройства на ряд более простых, поддающихся электродинамическому анализу. Эти простые устройства называют базовыми элементами. Матрицы рассеяния базовых элементов определяются без учета взаимо­действия между ними. Затем, с помощью специальных алгоритмов рассчитывают элементы матрицы рассеяния для объединения двух и более базовых элементов, т.е. всей сложной цепи. Следует отметить, что структура цепей СВЧ, как правило, благоприятствует , подобному расчленению, так как обычно они состоят из отдельных относительно простых элементов, соединенных друг с другом от­резками линий передачи. При составлении библиотеки базовых элементов используют одну из двух возможностей.

В первом случае каждый элемент цепи заменяют эквива­лентной схемой, состоящей, из сосредоточенных элементов L, С, R и отрезков эквивалентной линии. При этом решение электроди­намической задачи для базового элемента представляется в виде эквивалентной схемы, в виде приближенных формул и справочных ' данных, определяющих связь величин элементов эквивалентной схемы с геометрическими размерами базового элемента,, длиной волны и параметрами диэлектрического заполнения. В этом слу­чае большое количество базовых элементов цепей СВЧ может быть сведено к небольшому числу элементов эквивалентных схем. Преимуществами такого подхода является универсальность, воз­можность разумной идеализации эквивалентных схем, а недос­татками - потеря точности при использовании упрощенных эквива­лентных схем и трудности в количественной оценке погрешностей расчета.

Во втором случае на основе решения электродинамической задачи для каждого базового элемента аналитически или численно находится характеристическая матрица. При этом удается вы­полнять расчеты с любой требуемой точностью. Однако такой подход менее универсален и требует значительно большего объема вычислений. Отметим, что оба подхода не имеют глубоких прин­ципиальных различий.

Анализ каскадного соединения четырехполюсников. Рас­смотрим частный случай цепи СВЧ, достаточно часто встре­чающийся на практике,-каскадное соединение четырехполюс­ников, т.е. выход предшествующего элемента цепи соединяется со входом последующего и т.д. (рис. 12.29). Анализ каскадного сое­динения значительно упрощается, если описывать четырехпо­люсники не матрицей || S ||, а специальной матрицей передачи

|| А ||, которая связывает полные нормированные напряжения и токи на входе u_п1, i_п1 и на выходе u_п1, i_п1 четырехполюсника:

Для определения физического смысла элементов матрицы || A || рассмотрим некоторые частные случаи работы четырех­полюсника. Пусть сигнал от генератора подается на вход четы­рехполюсника (полюса 1^1), а выходные полюса его (2-2) оста­ются разомкнутыми. При этом i_п2=0 и из (12.50) следует, что А₁₁= u_п1/ i_п1. А₁₁ обычно называют коэффициентом передачи че­тырехполюсника по полному напряжению при размыкании его вы­ходных полюсов, т.е. A₂₁-нормированная проводи­мость четырехполюсника при размыкании его выходных полюсов. Если подать сигнал от генератора на вход четырехполюсника, а его выходные полюсы замкнуть накоротко, то при этом u_п2 = 0 и из (12.50) следует, что т.е. А₂₂-коэффициент пере­дачи четырехполюсника по полному току при КЗ на его выходе, а т.е. A₁₂ - нормированное сопротивление четырех­полюсника при КЗ на его выходе.

Нетрудно показать с помощью (12.50), что матрица передачи ||А|| четырехполюсника , образованного каскадным соединением двух четырехполюсников, имеющих матрицы передачи ||A₁|| и ||А₂||,

вычисляется по формуле ||А|| = || А₁||∙|| А₂||(рис.12.29). Это свой­ство матрицы передачи распространяется на любое число каскадно соединенных четырехполюсников.

Из (12.50) и (12.42), используя (12.9), получаются формулы, связывающие элементы матриц || S| | и ||А||, для произвольного четырехполюсника: S_U=(A_U+A₁₂-A_2i-A₂₂)/D,

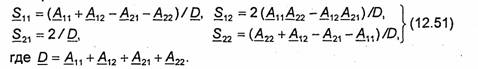
Итак, анализ каскадного соединения четырехполюсников сво­дится к вычислению на заданной частоте матрицы || А || для каждо­го элемента цепи, перемножению матриц отдельных элемен-тов, что определяет матрицу || А || всей цепи, нахождению элемен-тов

матрицы S всей цепи по формулам (12.51).

Характеристические матрицы эквивалентных схем неко­торых базовых элементов. При декомпозиции цепей СВЧ наибо­лее часто встречаются базовые элементы, имеющие следующие эквивалентные схемы.

1. Отрезок эквивалентной линии передачи (рис.12.30) длиной l является двухплечным устройством и может быть пред­ставлен четырехполюсником. Матрица ||S || для него имеет вид (12.43) при N=2. Пренебрегая тепловыми потерями в отрезке ли­нии и исходя из физического смысла элементов ||S||, получаем Из (12.51) находим элементы матрицы А через элементы матрицы || S ||. На рис.12.30 выписаны матрицы ||S|| и ||А||. Для получения матриц ||S || и ||А || отрезка эквивалентной линии с учетом потерь следует в выражениях для элементов матриц (рис. 12.30) заменить

2. Стык двух линий передачи с разными волновыми со­противлениями -двухплечное устройство (рис.12.31), которое можно представить четырехполюсником. Причем расстояние между плоскостями отсчета в плечах равно 0.

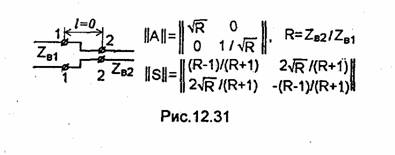
Матрица || S || имеет вид (12.43) при N=2. В плоскости стыка равны полные ненормиро­ванные напряжения и токи:U_п1 = U_п2 и i_п1 = -i_П2. Знак минус в по­следнем равенстве учитывает тот факт, что за положительные на­правления для тока на каждом входе выбраны направления внутрь четырехполюсника (см. рис. 12.28, б). Переходя в записанных ра­венствах к нормированным напряжениям и токам, согласно (12.39) получаем что позволяет найти элементы матрицы || А|| а по (12.51) и элементы || S|| (рис.12.31).

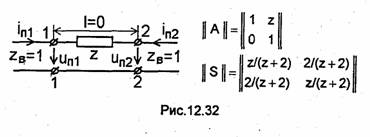
3. Четырехполюсник, образованный последовательно включенным сопротивлением Z в линию с волновым сопро­тивлением Z_B (рис. 12.32). Считаем расстояниеl между полюсами 1-1 и 2-2 равным нулю. В данном случае можно записать сле­дующие выражения, связывающие нормированные напряжения и токи на входе и выходе: Сравнивая это с (12.50), получаем из (12.51) находим элементы матрицы ||S|| (рис.12.32).

4. Четырехполюсник, образованный параллельно вклю­ченной проводимостью У в линию передачи с волновым соп­ротивлением Z_B (рис.12.33). Считаем расстояние l между полю­сами 1-1 и 2-2 равным нулю. Используя законы Кирхгофа для рассматриваемой цепи, запишем связь между нормированными напряжениями и токами на полюсах: где это позволяет определить элементы матрицы || А ||, а из (12.51) найти элементы матрицы || S || (рис.12.33).

Анализ произвольной цепи СВЧ. В этом случае цепь рас­членяется на базовые элементы, для которых заранее опреде­лены характеристические матрицы. Матрицы рассеяния некоторых часто встречающихся базовых элементов можно найти в [29,33]. Затем на ЭВМ с помощью специально составленной вычисли­тельной программы рассчитывают матрицу рассеяния всего уст­ройства. Основу алгоритмов для разработки таких программ со­ставляют формулы для расчета элементов матрицы ||S|| со­единения двух многополюсников с известными матрицами || S., || и || S₂||. Явные формулы для вычисления || S || через || S, || и || S₂|| приведены в [29,43]. Далее к полученному многополюснику при­соединяется третий базовый элемент с матрицей || S₃ J и нахо­дится матрица рассеяния для нового соединения, и так далее до тех пор, пока не будут присоединены все базовые элементы рас­сматриваемой цепи. В результате последовательного применения описанной процедуры может быть построена матрица рассеяния любого сложного соединения произвольного числа базовых эле­ментов. Варианты алгоритмов вычисления матриц рассеяния про­извольных линейных и пассивных цепей СВЧ по известным матри­цам рассеяния базовых элементов, отличающиеся организацией процесса вычисления ||S|| приведены в [36,43].