12.3. Матричное описание цепей свч

При построении математических моделей сложных цепей СВЧ обычно используют характеристические матрицы. Достаточно об­щую конструкцию произвольной цепи СВЧ можно представить в виде сочленения, образованного N линиями передачи, которые могут быть как одного, так и разных типов. На рис. 12.26 показано такое устройство, содержащее четыре подводящих линии (N=4). Линии передачи используются либо для подвода энергии от генератора к устройству, либо для подключения к нему внешних оконечных устройств (полезных нагрузок, поглощающих нагрузок, короткозамыкающих поршней и т.д.). Для построения математи­ческой модели рассматриваемого сочленения в каждой подводя­щей линии выбираем поперечное сечение, расположенное на некотором расстоянии от места сочленения. Проводим через эти сечения плоскости Т₁,Т₂.....T_N (рис.12.26), которые в дальнейшем будем называть плоскостями отсчета фаз элементов характе­ристических матриц. Предположим, что расстояние от плоскостей отсчета до сочленения выбрано так, что в этих плоскостях можно пренебречь амплитудами нераспространяющихся волн, которые могут возникать в месте сочленения линий. Рассмотрим уст­ройство, образовавшееся между плоскостями отсчета. Оно имеет N плеч, образованных отрезками линий передачи. Причем каждый свободный конец этих отрезков линии служит или входом, через который энергия вводится в устройство, или выходом, через который энергия выводится из него. Поскольку каждый отрезок линии может быть представлен отрезком эквивалентной линии, имеющей два входных зажима (полюса) на входе, то рассмат­риваемое устройство возможно представить эквивалентным многополюсником (рис.12.27). Причем если в каждом из N плеч устройства распространяется лишь один невырожденный тип вол­ны, то эквивалентный многополюсник имеет 2N полюсов, обоз-

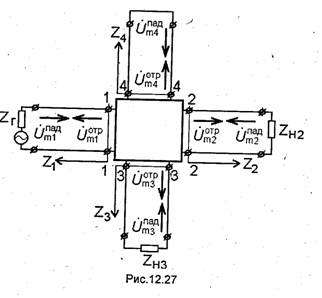
начаемых 1-1,2-2, ...,N-N. Рассмотрим случай, когда в одном или в нескольких плечах устройства будут распространяться несколько типов волн, т.е. линия, образующая такое плечо, ра­ботает в многоволновом режиме, или линия работает в одноволновом режиме, но по ней распространяются вырожденные волны (например, распространяющаяся по круглому волноводу волна H₁₁ с круговой поляризацией вектора Е в центре волновода может быть представлена суммой двух вырожденных распро­страняющихся волн H₁₁ с линейными взаимно перпендикулярными поляризациями векторов Е). При этом каждое плечо, в котором может распространяться несколько типов волн, следует пред­ставить в эквивалентном многополюснике несколькими входами или выходами по числу распространяющихся волн в плече; при этом многополюсник будет иметь 2n полюсов, где п >N.

Заменив линии передачи эквивалентными линиями, а гене­раторы, оконечные нагрузки, короткозамыкающие поршни их экви­валентными представлениями, получаем для рассматриваемого устройства (рис. 12.26) эквивалентную схему (рис. 12.27), при этом в каждой эквивалентной линии могут распространяться соответ­ствующие падающие и отраженные волны напряжений (токов). Поскольку мощность, переносимая волной напряжения (тока) по эквивалентной линии, зависит не только от амплитуды напряжения (тока) волны, но и от волнового сопротивления линии (12.2), обычно при рассмотрении свойств многополюсника, ко входам которого могут подключаться линии с разными значениями волнового сопротивления, вводят нормированные напряжение u(z) и ток i(z), распространяющиеся в каждой эквивалентной линии и связанные с напряжением U_m(z) и током i_m(z) с формулами

где Z_B - волновое сопротивление эквивалентной линии.

Величины u(z) и i(z) имеют одинаковую размерность √Вт, поэтому нормированное волновое сопротивление z_B эквивале­нтной линии, в которой распространяются нормированные нап­ряжение и ток, будет безразмерной величиной, равной 1:

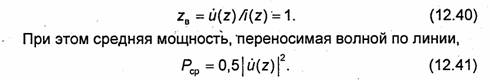
Введем в каждой линии передачи (см. рис. 12.26) соответ­ствующую систему координат так, чтобы продольная ось была направлена от сочленения, а ее начало было расположено в плоскости отсчета фаз рассматриваемой линии. При этом начало

отсчета продольных осей Z₁Z₂.....Z_N в эквивалентной схеме (рис.12.27) совмещено с соответствующими полюсами 1-1,2-2, ...,N-N. Будем называть волны, распространяющиеся в плечах в сторону многополюсника, падающими, а волны, распространяю­щиеся от многополюсника,-отраженными. Пусть генератор соз­дает в линии 1, подключенной к плечу 1 многополюсника, па­дающую волну напряжения..Эта волна, дойдя до сочленения, будет частично отражаться, вызывая в линии 1 отраженную волну, а частично, пройдя через многополюсник, поступит на выходы остальных плеч, вызывая в подключенных к ним линиях отра­женные волны напряжений. Эти волны, в свою очередь, рас­пространяясь по линиям, подключенным к плечам 2, 3,..., N много­полюсника, будут в общем случае частично поступать в оконечные нагрузки, а частично отражаться от них, вызывая в линиях па­дающие волны напряжения. В свою очередь, падающие волны в линиях, подключенных к плечам 2, 3.....N, будут на входах много­полюсника частично отражаться от сочленения, а частично про­ходить через него, вызывая отраженные волны в линиях, под­ключенных к плечам многополюсника, и т.д. Таким образом, в каждой плоскости отсчета устройства (см. рис.12.26) или на входах каждой пары полюсов в эквивалентной схеме (см. рис.12.27) будут действовать падающая и отраженная волны, которые будем характеризовать нормированными функциями и_j^пад и u_j°^тр, где j=1, 2, ...,N(рис.12.28,а). Каждая из указанных волн представляет

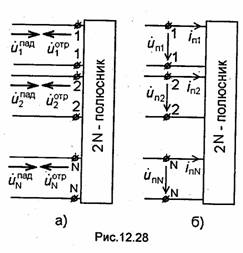
собой суперпозицию волн, соз­данных как непосредственно генератором, так и оконечными нагрузками линий, подключен­ных к выходам устройства. Сог­ласно (12.9) и (12.10) в плос­костях отсчета или на полюсах многополюсника можно ввести полные нормированные напря­жения u_п1, u_п2, ..., u_nN и токи (рис. 12.28, б).

В общем случае режим ра­боты каждого входа много­полюсника можно описать с

помощью двух комплексных величин, например, для j-го входа это могут быть или

Поэтому можно ввести несколько различных описаний много­полюсника, считая в каждой выбранной паре одну из величин независимой, а вторую зависимой. Наибольшее применение в технике СВЧ при описании свойств многополюсников нашла волновая матрица рассеяния || S ||, устанавливающая связь между нормированными напряжениями отраженных и падающих волн во всех плоскостях отсчета устройства или на всех полюсах его эквивалентной схемы.

Если рассматриваемое N-плечное устройство является пас­сивным и линейным (содержит лишь линейные среды), то в силу линейности уравнений Максвелла нормированное напряжение отраженной волны u_j°^тр в плоскости отсчета j-го плеча (на полюсах j-j многополюсника) можно рассматривать как суперпозицию волн_, образовавшихся под воздействием падающих волн в плоскостях отсчета всех плеч устройства (на всех полюсах многополюсника при n = N):

где безразмерные комплексные ве­личины, не зависящие от нормированных напряжений падающих и отраженных волн. Систему из N уравнений (12.42), устанав­ливающую связь между напряжениями падающих и отраженных волн на входах многополюсника, удобно записать в матричном виде:

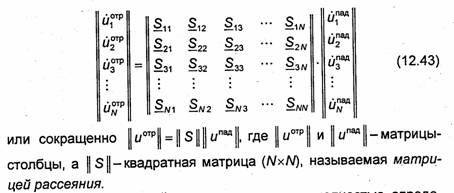
Передаточные свойства многополюсника полностью опреде­лены, если известна его матрица ||S ||, записанная для выбранной системы плоскостей отсчета в каждом плече на заданной частоте. Вид матрицы не зависит от подключаемых к многополюснику устройств. Определиим физический смысл элементов S_jq матрицы рассеяния. Для этого рассмотрим частный случай работы многополюсника (рис.12.28, а): пусть к полюсам j-j подключен генератор, а к полюсам всех остальных плеч подключены сог-

S_qj-коэффициент передачи по нормированному напряжению от полюсов j-j к полюсам q-q многополюсника (от плоскости отсчета в плече q к плоскости отсчета в плече q устройства) при заданных выше условиях.

Рассмотренная выше матрица рассеяния называется нор­мированной, поскольку она устанавливает связь между нормиро­ванными напряжениями. Иногда вводят [33] ненормированную матрицу || S||, связывающую ненормированные напряжения отра­женных и падающих волн в плоскостях отсчета каждой линии. В дальнейшем будут рассматриваться лишь нормированные мат­рицы. Для таких матриц согласно (12.44) и (12.41) что совпадает с

коэффициентом передачи по мощности из плеча j в плечо q устройства при условии, что мощность (P_j^пад)_Cp подается на вход плеча j ,а во всех остальных плечах падающие волны отсутствуют. Поэтому для всех элементов матрицы рессеяния выполняется условие | S_qj| ≤1. Для ненормированной матрицы величина | S_qj |зависит не только от отношения мощностей (P_q^отp)_cp и(Рj^пад)_ср, но и от волновых сопротивлений линий, подключенных к полюсам j-j и q-q многополюсника.

Кроме матрицы ||s|| в технике СВЧ используют матрицу * сопротивлений и матрицу проводимостей. Матрица сопротив­лений ||z|| устанавливает связь между полными нормированными напряжениями и токами на всех входах многополюсника (см. рис. 12.28, б):

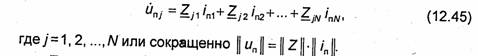
Последнее соотношение напоминает описание цепи с по­мощью матрицы сопротивлений в классической теории цепей [28]. Это позволяет с заданным многополюсником сопоставить неко­торую цепь, называемую эквивалентной схемой, имеющую такую же матрицу сопротивлений. Следует отметить, что переход от многополюсника к эквивалентной схеме неоднозначен, так как имеется множество схем с одинаковыми матрицами сопро­тивлений. Эквивалентность между многополюсником и цепью, строго говоря, существует только на одной частоте, однако в некотором приближении можно рассматривать и узкую полосу частот вблизи этой частоты. Матрица проводимостей ||Y|| уста­навливает связь между полными нормированными токами и напряжениями на всех входах многополюсника (рис. 12.28, б):

где j = 1,2,'...,N, или сокращенно || i_п || = || У || • || и_п ||. Хотя по аналогии с низкочастотными цепями можно определить физический смысл элементов матриц || Z|| и || У||, как сделано в [16], однако в общем случае в диапазоне СВЧ элементы этих матриц имеют фор­мальный смысл, поскольку формальный смысл имеют и нормиро­ванные напряжения и токи в произвольной линии передачи. Напротив, элементы матрицы ||S|| имеют выясненный выше фи­зический смысл в любом случае.

Матрицы ||Z|| и || У|| обычно более удобны при анализе пос­ледовательного или параллельного соединения многополюсников

[33]. Используя (12.9) и (12.10), легко установить связь между матрицами [34]:

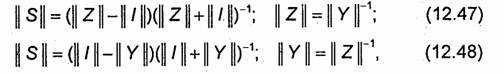
где ||/|| -единичная квадратная матрица порядка N, а (|| Z|| +||/||)^-1-матрица, обратная матрице (|| Z|| + || /|).

Изменение положения плоскостей отсчета в плечах мно­гополюсника. Характеристические матрицы многополюсника оп­ределяются для выбранного заранее положения плоскостей от­счета в каждом плече Т₁Т₂, ...,T_N (см. рис.12.26). На практике очень часто при экспериментальном определении элементов матриц многоплечных устройств бывает затруднительно, а иногда и невозможно измерить те или иные величины в поперечных сечениях линий, где расположены плоскости отсчета. Как правило, между измерительной аппаратурой и поперечным сечением, где расположена плоскость отсчета, оказывается включенным допол­нительный отрезок линии передачи. Из-за этого измеренные величины относятся к новым плоскостям отсчета, сдвинутым в ту или иную сторону вдоль линии передачи относительно старых плоскостей отсчета. Поэтому возникает необходимость преобра­зования известной матрицы устройства относительно введенных новых плоскостей отсчета. Наиболее просто такое преобразование выполняется для элементов матрицы || S ||. Пусть в каждом плече j (j = 1,2.....N) на расстоянии ∆z_j, от старой плоскости отсчета Тj) (см. рис. 12.26) введена новая плоскость отсчета Tj, причем при ∆z_j>0 новая плоскость расположена дальше от сочленения, а при ∆z_j<0-ближе к сочленению относительно старой плоскости. Матрицу рассеяния устройства относительно новых плоскостей

Отсюда следует, что при смещении плоскостей отсчета изменяются аргументы элементов матрицы ||S ||из-за изменения

путей, проходимых падающими и отраженными волнами в плече устройства. Кроме того, из-за наличия затухания в линиях передачи изменяются и модули элементов матрицы. При малых ∆Zj можно пренебречь потерями в отрезках линий (α_j≈0) в этом случае смещение плоскостей отсчета в плечах устройства при­водит лишь к изменению аргументов элементов матрицы || S ||.

Основные свойства характеристических матриц. 1. Пас­сивный многополюсник, выполненный на основе изотропных материалов, является взаимным; в этом случае S_jq = S_qj для любых jи q. Для такого многополюсника матрица || S || будет симметрической, т.е. ||S| |= ||S|^T, где || S||^т-транспонированная матрица |S||. Матрицы ||Z|| и || У ||также будут симметрическими. Многополюсник, содержащий анизотропный материал (например, намагниченный постоянным магнитным полем феррит), является невзаимным, его характеристические матрицы не будут сим­метрическими (S_jq ≠S_qJ).

2. Матрица рассеяния || S || многополюсника без потерь (с изотропным или анизотропным заполнением) является унитарной, для нее справедливо || S* ||^т • || S || = || /1||, где || S* ||^т - комплексно-сопряженная транспонированная матрица || S ||; это равенство является следствием закона сохранения энергии. Действительно, на его основе можно записать

Элементы матриц ||Z|| и || У|| для многополюсника без потерь

будут чисто мнимыми величинами. Более подробно с характе-, ристическими матрицами можно ознакомиться в [32, .33].