12.1.3. Полное эквивалентное сопротивление линии передачи

Процесс распространения волн в линии передачи, нагру­женной на произвольное сопротивление Z_H, может характери­зоваться с помощью полного эквивалентного сопротивления линии Z_n(z), которое в заданном сечении линии равно отношению

комплексных амплитуд полного напряжения и полного тока в этом сечении. Используя (12.9) и (12.10), запишем формулу, связы­вающую полное сопротивление с коэффициентом отражения в произвольном сечении линии:

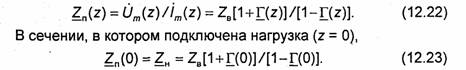
Из (12.23) следует формула, которая позволяет определить модуль Г_о и аргумент щ коэффициента отражения по известной величине Z_H:

Подставляя в (12.22) выражение (12.14) и учитывая равенство (12.24), запишем формулу для вычисления полного эквивалент­ного сопротивления в произвольном сечении линии:

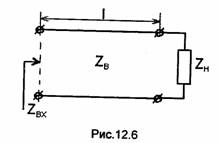
Отметим, что полное сопротивление в произвольном сечении линии называют эквивалентным, поскольку если линию рассечь в этом сечении, то входное сопротивление образовавшегося справа от сечения отрезка линии, нагруженного на Z_H (рис. 12.6), будет равно полному сопротивлению линии в этом сечении, т.е. Z_BX=Zn(z).

Часто при вычислении сопротивлений (полных, входных и т.д.) используют их нормированные значения, т.е. отнесенные к некоторому нормировочному сопротивлению Z_BH; например, нор­мированное полное сопротивление Z_n(z) = Z_n(z)/Z_eH, нормиро­ванное волновое сопротивление линии Z_B = Z_B/Z_BH, нормированное сопротивление нагрузки z_H=Z_H/Z_BH. Как правило, для рас­сматриваемой линии (см. рис.12.1,а) выбирают Z_BH=Z_B, при этом z_B = 1. Однако в некоторых случаях, например если цепь СВЧ включает каскадное соединение нескольких отрезков линий с разными волновыми сопротивлениями, в качестве Z_BH для всей цепи выбирают Z_B одного из них.

В ряде случаев удобно оперировать не полным эквивалент­ным сопротивлением в произвольном сечении линии, а полной эквивалентной проводимостью в этом сечении:

или нормированной полной эквива­лентной проводимостью: y(z)=1/z_n(z).

Полное эквивалентное сопроти­вление в заданном сечении линии зависит от расстояния между этим сечением и нагрузкой. Поэтому отре­зок линии длиной l (см.рис.12.6) можно использовать для трансформации (преобразования) величины сопротивления нагрузки Z_H. Например, при α = 0 входное сопротивление Z_BX отрезка линии длиной l равно полному сопротивлению, рассчитываемому по (12.26) при z=l Аналогично по (12.25) при z=l можно рассчитать входное сопротивление отрезка с учетом тепловых потерь в нем. Как следует из (12.26), при Z_H=Z_B входное сопротивление отрезка равно Z_B при любой его длине l и любой рабочей частоте.

Рассмотрим некоторые частные случаи трансформирующих отрезков.

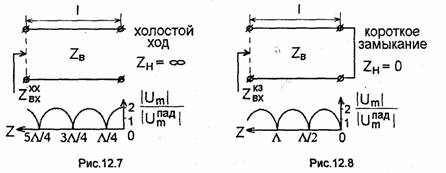
1. Короткозамкнутые и разомкнутые на конце отрезки линии (реактивные шлейфы). На рис.12.7 и 12.8 показаны отрезки эквивалентной линии, называемые реактивными шлей­фами, на конце которых или режим холостого хода (XX) при Z_H = ∞

(рис.12.7) или режим короткого замыкания (КЗ) при Z_H = 0 (рис. 12.8). Волновое сопротивление отрезков линии равно Z_B. Из (12.24) следует, что в случае XX на конце линии Г(0) ⁼ 1> т.е. Г_о = 1, ψ_о = О; а в случае КЗ Г(0)⁼-1. т.е. Г_о = 1, ψ_о = π. Падающая волна, распространяющаяся по реактивному шлейфу, полностью отража­ется от его конца; при этом в шлейфе устанавливается режим стоячей волны. Входное сопротивление шлейфов при а = 0 можно определить из (12.26), подставляя zl.

Как видно, входное сопротивление чисто реактивное, т.е. либо индуктивное либо емкостное, и зависит от длины отрезка и рабочей частоты.

Из формул (12.28) следует соотношение позво­ляющее по известным (например, измеренным) входным сопро­тивлениям отрезка в режимах КЗ и XX определить волновое сопротивление отрезка.

Отметим, что режим КЗ для отрезков реальных линий можно осуществить, поместив в конце металлическую пластину, располо­женную перпендикулярно продольной оси линии и имеющей конконтакт с ее стенками.

В полосковых линиях режим, близкий к режиму короткого замыкания, можно обеспечить, соединяя полоску с экранирующими пластинами с помощью металлического провод­ника (перемычки). В случае линий с ТЕМ-волной, поперечные размеры которых достаточно малы по сравнению с длиной волны, режим, близкий к режиму XX, можно обеспечить путем обрыва линий. В линиях с волнами Е или Н такой режим обеспечить не удается.. Отрезок любого волновода, открытый на конце, при распространении по нему Е- или Н-волн имеет эквивалентную схему, показанную на рис.12.6, поскольку часть мощности, пере­носимая падающей волной, будет излучаться в открытое прост­ранство, а оставшаяся часть будет отражаться от открытого конца отрезка обратно, т.е. в этом случае Г_о< 1.

2. Четвертьволновый отрезок линии передачи. Если длина отрезка l=Λ/4, величина βl=π/2, при этом входное сопротивление отрезка

Такой отрезок называют четвертьвол­новым трансформатором или инвертором сопротивления, пос­кольку его входное сопротивление пропорционально проводи­мости нагрузки, подключенной к его концу. Для четвертьволнового реактивного шлейфа из (12.28) следует, что Поэтому в линиях с TЕМ-волнами режим КЗ в конце линии можно обеспечить либо закоротив проводники, либо подключив к концу линии четвертьволновый отрезок, разомкнутый на конце. Хотя второй способ выглядит менее привлекательно, при проектиро­вании устройств на основе полосковых линий его применяют намного чаще. При этом не нарушается плоская форма конст­рукции и не требуются дополнительные технологические операции для установки металлической перемычки между полоской и экра­нами, как в первом случае.

3. Полуволновый отрезок линии передачи. Для отрезка линии длиной l=Λ/2 (см. рис.12.6), называемого полуволновым трансформатором, величина βl=π; его входное сопротивление Z_BX=Z_H, т.е. такой отрезок при любом Z_B на расчетной частоте трансформирует сопротивление нагрузки само в себя.