Лабораторная работа №5 Марковские случайные процессы с конечным множеством состояний и непрерывным временем.

Теоретические сведения. Функционирование системы можно рассматривать как последовательное изменение во времени её состояний. Если количество возможных состояний системы X_j j= конечно, а переход из одного состояния в другое может происходить в любой момент времени, то такие процессы называются СП с конечным множеством состояний и непрерывным временем. Расчёты таких процессов значительно упрощаются, если СП являются марковскими.

Пусть имеется случайный процесс, протекающий в системе с возможными состояниями X₀ ,X₁ ,…X_i ,…X_j ,…. Обозначим условную вероятность того, что в момент t=t₀+ система будет в состоянии X_j , если в момент t₀ она находилась в состоянии X_i через P_ij(t₀, ) . СП называется марковским, если эта вероятность P_ij(t₀, ) зависит только от i, j, t₀ ,, то есть только от того, в каком состоянии система была в момент t₀ и в какое состояние она перейдёт через время .

Для описания поведения системы в классе марковских дискретных процессов с непрерывным временем необходимо:

1. Ввести понятие состояния системы.

2. Указать все состояния, в которых может находится система.

3. Составить граф состояний, то есть указать пути возможных непосредственных переходов системы из состояния в состояние.

4. Для расчёта переходных процессов в системе указать, в каком состоянии находится система в начальный момент времени.

5. Для каждого возможного перехода на графе указать интенсивность _ij потока событий, переводящих систему из состояния X_i в состояние X_j . Обычно интенсивности _ij определяются экспериментально.

Исчерпывающей характеристикой марковского процесса является совокупность вероятностей P_j(t) того, что процесс в момент времени t будет находится в состоянии X_j j= . Эти вероятности определяются на основе решения системы дифференциальных уравнений:

(1)

(2)

Система (1) определяет переходной процесс в предположении, что начальное состояние – Р₀.

Если число состояний системы n – конечно и из каждого состояния графа можно перейти в любое другое состояние, то такая система будет иметь предельный стационарный режим. Так, система рис.1а имеет стационарный режим, а система рис.1б – не имеет.

а) б)

Рис.1

С практической точки зрения представляет интерес определение вероятностей состояний системы в предельном стационарном режиме.

Для их расчёта используется система алгебраических уравнений, получающаяся из (1) путём приравнивания нулю производных:

(3)

Система (3) является линейно зависимой, поэтому её следует дополнить условием:

(4)

Постановка задачи. Система с конечным множеством состояний X_j j= и непрерывным временем задана графом состояний и переходов. Заданы также интенсивности переходов _ij и начальное состояние системы – Х_k. Требуется рассчитать переходной процесс в системе P_j(t) j= , а также вероятности состояний P_j j= в предельном стационарном режиме.

Методика решения задачи.

1. Для заданного графа состояний и переходов составляется система дифференциальных уравнений:

2. Полученная система является линейно-зависимой. Поэтому в ней исключается одна из переменных и соответствующее ей дифференциальное уравнение. Вместо него используется связь:

Например, для определённости в системе уравнений исключим Р₀(t) подстановкой

Тогда получим:

3. Переходной процесс в системе может быть рассчитан методом Эйлера. При этом расчетные соотношения будут иметь вид:

где g=0,1,2,3… - номер итерации;

- шаг квантования по времени. Начальные условия задаются в соответствии с исходными данными, то есть

Переходной процесс рассчитывается до тех пор, пока вероятности Р_j^g практически перестанут изменяться.

4. Вероятности Р_j состояний системы в предельном стационарном режиме определяются путём решения системы алгебраических уравнений, которая получается приравниванием нулю производных в системе дифференциальных уравнений:

(5)

Указание. Граф состояний и переходов, интенсивности переходов _ij и шаг квантования задаются преподавателем.

Пример:

Задан следующий граф:

Начальное состояние – Х₂, ∆t = 0,05.

1. Для заданного графа состояний и переходов система дифференциальных уравнений имеет вид:

2. В системе уравнений исключаем подстановкой:

И система примет вид:

3. Переходной процесс выполним методом Эйлера (вычисления следует выполнять программно, так как g может принимать большие значения).

4. Вероятности Р_j состояний системы в предельном стационарном режиме определим, решая систему алгебраических уравнений:

Листинг программы, написанной в среде Matlab 6.1.:

clear;

g=1;

p1(g)=0; %начальные значения

p2(g)=1;

p3(g)=0;

p0(g)=1-p1(g)-p2(g)-p3(g);

dt=0.05; %шаг

for i=1:200

p1(g+1)=p1(g)+dt*((-0.7-0.4-0.5)*p1(g)+0.3*(1-p1(g)-p2(g)-p3(g))+0.2*p2(g));

p2(g+1)=p2(g)+dt*((-0.2-0.8)*p2(g)+0.5*p1(g)+0.3*p3(g));

p3(g+1)=p3(g)+dt*(-0.3*p3(g)+0.7*(1-p1(g)-p2(g)-p3(g))+0.4*p1(g));

p0(g+1)=1-p1(g+1)-p2(g+1)-p3(g+1);

g=g+1;

end;

x=0:200;

p0=1-p1(g-1)-p2(g-2)-p3(g-3);

disp(' # p0 p1 p2');

[x' p1' p2' p3']

[p0 p1(g-1) p2(g-2) p3(g-3)]

a=[1 1 1 1; 0.3 -1.6 0.2 0; 0 0.5 -1 0.3; 0.7 0.4 0 -0.3]; %матрица коэффициентов состояний системы в предельном стационарном режиме

b=[1; 0; 0; 0];

p=a\b %решение системы

sum(p) %сумма вероятностей

Результат работы программы:

# p0 p1 p2

0 0 1.0000 0

1.0000 0.0100 0.9500 0

2.0000 0.0193 0.9027 0.0016

3.0000 0.0279 0.8581 0.0046

4.0000 0.0359 0.8160 0.0089

5.0000 0.0433 0.7762 0.0144

6.0000 0.0501 0.7387 0.0209

7.0000 0.0563 0.7033 0.0282

8.0000 0.0620 0.6700 0.0363

9.0000 0.0672 0.6386 0.0451

10.0000 0.0720 0.6090 0.0545

11.0000 0.0763 0.5812 0.0644

12.0000 0.0802 0.5550 0.0747

13.0000 0.0836 0.5304 0.0853

14.0000 0.0868 0.5072 0.0963

15.0000 0.0895 0.4855 0.1074

16.0000 0.0920 0.4651 0.1187

17.0000 0.0942 0.4459 0.1301

18.0000 0.0960 0.4279 0.1416

19.0000 0.0976 0.4110 0.1531

20.0000 0.0990 0.3952 0.1646

21.0000 0.1002 0.3804 0.1760

22.0000 0.1011 0.3665 0.1874

23.0000 0.1019 0.3535 0.1987

24.0000 0.1024 0.3414 0.2099

25.0000 0.1028 0.3300 0.2209

26.0000 0.1031 0.3194 0.2317

27.0000 0.1032 0.3095 0.2424

28.0000 0.1033 0.3002 0.2529

29.0000 0.1031 0.2916 0.2632

30.0000 0.1029 0.2835 0.2733

31.0000 0.1026 0.2760 0.2832

…

177.0000 0.0616 0.1943 0.5454

178.0000 0.0616 0.1943 0.5454

179.0000 0.0616 0.1943 0.5455

180.0000 0.0616 0.1943 0.5455

181.0000 0.0616 0.1943 0.5455

182.0000 0.0616 0.1943 0.5455

183.0000 0.0616 0.1944 0.5455

184.0000 0.0616 0.1944 0.5455

185.0000 0.0616 0.1944 0.5455

186.0000 0.0616 0.1944 0.5455

187.0000 0.0616 0.1944 0.5455

188.0000 0.0615 0.1944 0.5455

189.0000 0.0615 0.1944 0.5455

190.0000 0.0615 0.1944 0.5455

191.0000 0.0615 0.1944 0.5455

192.0000 0.0615 0.1944 0.5455

193.0000 0.0615 0.1944 0.5455

194.0000 0.0615 0.1944 0.5455

195.0000 0.0615 0.1944 0.5455

196.0000 0.0615 0.1944 0.5455

197.0000 0.0615 0.1944 0.5455

198.0000 0.0615 0.1944 0.5455

199.0000 0.0615 0.1944 0.5455

200.0000 0.0615 0.1944 0.5455

[p0 p1 p2 p3] =

0.1986 0.0615 0.1944 0.5455

p =

0.1986

0.0615

0.1944

0.5455

sum(p)= 1

Вероятности переходного процесса (Рис.1) при g > 200 стремятся к вероятностям предельного стационарного режима работы системы. Следовательно, вычисления были сделаны верно.

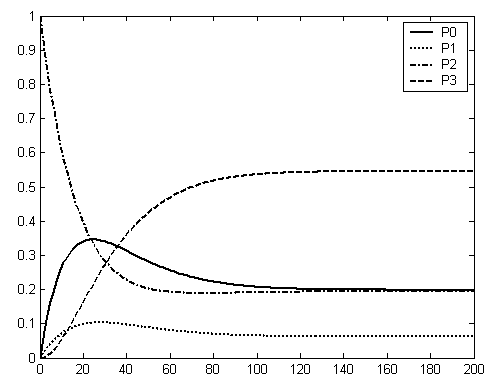
Рис.1. График сходимости метода Эйлера