Лабораторная работа №4 Параметрическая оптимизация динамической системы по критерию «сигнал/шум» на ее выходе

Т еоретические сведения. В реальных условиях полезный сигнал, поступающий на вход информационно-управляющей системы, часто оказывается зашумленным. Другими словами, входной сигнал системы представляет собой сумму полезного сигнала a(t) и случайного процесса (шума) X(t):

Y(t) = a(t) + X(t)

Если динамическая система линейная, то ее выходной сигнал Z(t) также будет состоять из двух составляющих: реакции системы на полезный сигнал a´(t) и на шум X´(t):

Z(t) = a´(t)+ X´(t)

Оптимизационная задача состоит в определении таких значений параметров системы, при которых энергетическое отношение «полезный сигнал/шум» на выходе системы будет максимальным. Таким образом, критерий оптимизации представляет собой выражение:

(1)

Чтобы конкретизировать задачу (1), необходимо задать: математическую модель системы, модель полезного сигнала a(t) и модель помехи на входе X(t).

Модель линейной системы обычно задается в виде дифференциального уравнения:

(2)

Модель полезного сигнала a(t) представляет собой явную функцию времени и может быть задана либо аналитически, либо графически.

Модель помехи X(t) есть СП и определяется своими характеристиками: корреляционной функцией или спектральной плотностью. Распространенной моделью помехи является так называемый «белый шум» - СП, имеющий постоянную спектральную плотность - const на любой частоте.

Для большинства практических задач критерий I конкретизируется следующим образом. Энергия полезного сигнала на входе системы принимается равной квадрату уровня a´(t) в определенный момент времени t₀ , т.е.

(3)

Обычно t₀ - это момент времени, когда уровень выходного сигнала a´(t) максимальный. Выражение для a´(t) получается путем решения дифференциального уравнения (2).

Для вычисления дисперсии помехи на выходе D[X´(t)] используются соотношения:

(4)

(5)

и - спектральные плотности входного и выходного СП соответственно; - квадрат модуля частотной характеристики системы.

Постановка задачи. Линейная динамическая система по каналу «вход-выход» описывается дифференциальным уравнением второго порядка:

(6)

k, T₁, T₂ – параметры.

На вход системы действует полезный сигнал a(t) вида:

а также помеха типа «белый шум» со спектральной плотностью .

Требуется исследовать зависимость критерия (1) (отношение «сигнал/шум» на входе системы) от одного из параметров системы - k, T₁, T₂. В выражении (1) принять Т = t₀. Сделать выводы.

Методика решения задачи.

1. Сформируем выражение для реакции системы на входное воздействие a(t) = A на интервале времени 0Т. При нулевых начальных условиях решение уравнения (6) имеет вид:

Для момента времени t₀ = T уровень полезного сигнала на выходе равен:

(7)

2. Найдем дисперсию шумов на выходе системы D[X´(t)] по выражениям (4) и (5). Для этого предварительно найдем модуль частотной характеристики системы. Передаточная функция системы (6):

Частотная характеристика получается заменой p на jω:

Модуль частотной характеристики равен:

Квадрат модуля:

С учетом того, что , выражение для спектральной плотности шумов на выходе согласно (4) имеет вид:

Дисперсия шумов на выходе системы согласно (5) равна:

(8)

3. С учетом (7) и (8) составляется выражение для критерия (1):

4. Для исследования зависимости I от параметра системы θ необходимо построить график функции I(θ) и выполнить его анализ. Здесь θ – один из параметров системы - k, T₁, T₂.

Указание. В качестве исходных данных должны быть заданы:

- А,Т – параметры входного сигнала a(t);

- S₀ – параметр помехи „белый шум”;

- значения двух из трех параметров системы.

Пример:

Заданы следующие значения параметров:

A = 0,5; T =10; S₀ = 0,2; k = 2; T₁ = 1,5.

Т₂ – неизвестный параметр.

По формуле (7) имеем:

По формуле (8) имеем:

Тогда критерий (1) примет вид:

Чтобы исследовать зависимость критерия (1) от неизвестного параметра системы, построим график зависимости I(T₂):

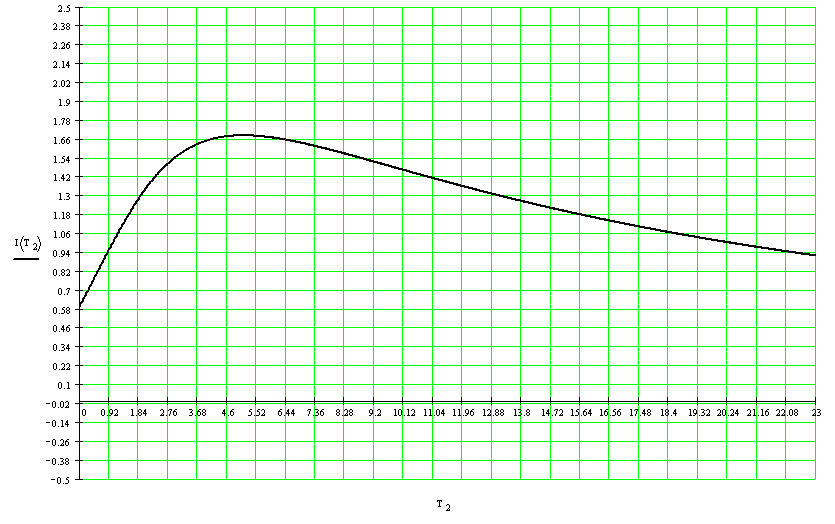
Рис.1. График зависимости I от Т₂

Выводы: Параметр I принимает оптимальное значение, равное 1,685, при T₂ равном 5,06.