Лабораторная работа №3 Преобразование характеристик ссп линейной динамической системой

Т

Система

еоретические сведения. Пусть на вход динамической системы поступает случайный процесс X(t) с известными характеристиками.

Е

X(t)

Y(t)

сли оператор (математическая модель) системы известна, то можно определить характеристики выходного сигнала Y(t),

который будет также представлять собой СП. Эта задача может быть решена с помощью различных подходов в зависимости от вида СП X(t) на входе системы и вида ее математической модели. В частном случае, когда X(t) представляет собой стационарный случайный процесс ССП, а оператор системы – линейный, решение задачи определения характеристик Y(t) (который также является ССП) может быть основано на использовании известного соотношения:

, (1)

где - модуль амплитудно-частотной характеристики системы; - спектральные плотности ССП X(t) и Y(t).

Для линейной системы частотная характеристика может быть непосредственно получена из ее дифференциального уравнения:

В операторной форме:

Для получения частотной характеристики системы в передаточной функции

оператор дифференцирования p заменяется на мнимую величину (jω):

Для определения других характеристик выходного сигнала Y(t), кроме соотношения (1) используются также преобразования Фурье:

(2)

(3)

Постановка задачи. На вход линейной динамической системы, описываемой дифференциальным уравнением, поступает ССП X(t), заданный реализацией на интервале 0÷Т. Требуется определить оценку корреляционной функции и спектральной плотности реакции (выхода) системы Y(t). Построить их графики.

Методика решения задачи.

1. Непрерывный ССП на входе системы X(t) представляется в виде m последовательных равноотстоящих отсчетов с шагом . Опытные данные, таким образом, преобразуются в одномерный массив X_j .

2. Определяется оценка корреляционной функции входного сигнала по формуле:

- оценка математического ожидания ССП X(t).

3. Определяется оценка спектральной плотности ССП X(t) по известной с помощью (3):

- шаг квантования по частоте.

4. По дифференциальному уравнению системы определяется ее частотная характеристика W(jω), а затем квадрат ее модуля . Для линейной системы квадрат модуля частотной характеристики будет представлять собой отношение полиномов частоты, т.е.:

5. По формуле (1) определяется оценка спектральной плотности выходного сигнала Y(t):

6. По формуле (2) преобразования Фурье определяется оценка корреляционной функции ССП Y(t):

7. Строятся графики:

Указание: непрерывная реализация ССП X(t) на интервале 0Т, дифференциальное уравнение линейной системы, а также параметр задачи m задается преподавателем.

Пример:

Дана следующая непрерывная реализация ССП X(t) на интервале 0Т (Т = 30):

дифференциальное уравнение линейной системы:

параметр задачи m = 30

1. По данному графику сделаем m замеров значений ССП X(t):

2. Найдем характеристики ССП X(t):

Математическое ожидание:

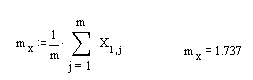
Оценка корреляционной функции:

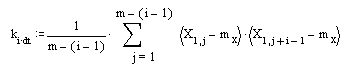
Оценка спектральной плотности:

3. По дифференциальному уравнению системы определим ее частотную характеристику W(jω):

,

а затем квадрат ее модуля :

,

где модуль комплексного числа вычисляется по формуле:

4.Определим необходимые характеристики выходного сигнала Y(t):

4.1. Оценка спектральной плотности

Строим графики:

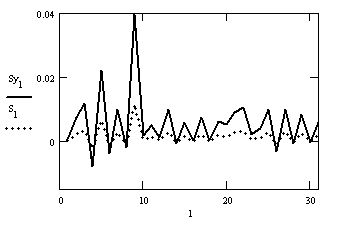
Рис.1. Оценки спектральной плотности ССП X(t) и Y(t)

Оценка корреляционной функции ССП Y(t)

Строим графики:

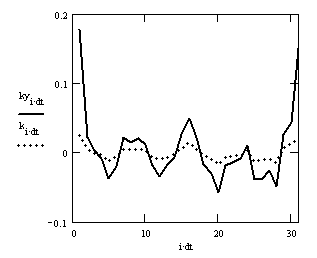
Рис.2. Оценки корреляционных функций ССП X(t) и Y(t)