Лабораторная работа №1 Определение характеристик случайных функций по опытным данным

Теоретические сведения. При решении прикладных задач наиболее часто используются следующие характеристики случайных функций (СФ):

1. Математическое ожидание СФ X(t) есть неслучайная функция m_X(t), равная для каждого значения аргумента t математическому ожиданию соответствующего сечения СФ – m_X(t)=M[X(t)].

2. Дисперсия СФ X(t) есть неслучайная функция D_X(t), равная для каждого значения аргумента t дисперсии соответствующего сечения СФ – D_X(t)=D[X(t)].

3. Корреляционная (автокорреляционная) функция СФ X(t) есть неслучайная функция двух аргументов K_X(t,t´), равная для каждой пары своих аргументов корреляционному моменту соответствующих сечений СФ – .

4. Для оценки взаимной связи (статистической зависимости) двух СФ X(t) и Y(t) используется характеристика – взаимокорреляционная функция. Это есть неслучайная функция двух аргументов R_XY(t,t´), равная для каждой пары своих аргументов корреляционному моменту соответствующих сечений СФ X(t) и Y(t´), т.е.

.

Постановка задачи. На интервале изменения аргумента (0Т) получены n реализаций СФ X(t) и Y(t). По этим опытным данным выполнить оценку характеристик СФ X(t) – m_X(t), D_X(t), K_X(t,t´), и Y(t) – m_Y(t), D_Y(t), K_Y(t,t´), а также взаимокорреляционной функции и построить их графики.

Методика решения задачи.

1. Диапазон изменения аргумента t разбивается на m равноотстоящих отсчетов t_j с шагом . Тогда непрерывные реализации СФ X(t), Y(t) необходимо представить в виде двумерных массивов: X_ij , Y_ij , где - номер отсчета, - номер реализации.

2. Определяется оценка математического ожидания СФ X(t) по формуле:

3. Определяется оценка дисперсии СФ X(t) по формуле:

и есть одномерные массивы размером m.

4. Определяется оценка автокорреляционной функции СФ X(t) по формуле:

5. Определяется оценка взаимокорреляционной функции СФ X(t) и Y(t) по формуле:

и есть двумерные массивы размером , - симметрична относительно главной диагонали.

Указание: непрерывные реализации СФ X(t) и Y(t), а также параметры задачи n, m задаются преподавателем.

Пример:

Даны следующие непрерывные реализации СП X(t) и Y(t) на интервале 0Т (Т = 30), n = 3, m = 30:

По данному графику сделаем m замеров значений СФ X(t) и Y(t).

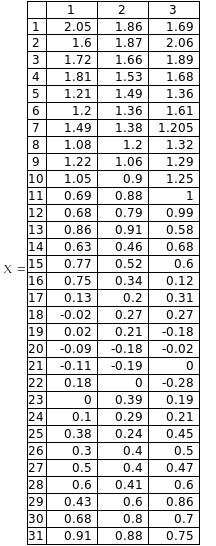
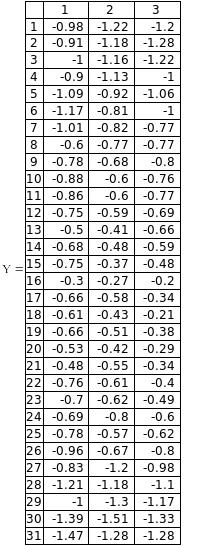
1. Вычислим оценки математических ожиданий СФ X(t) и Y(t).

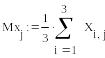
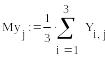
2. Вычислим оценки дисперсий СФ X(t) и Y(t).

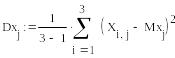
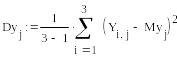
3. Вычислим оценки автокорреляционных функций СФ X(t) и Y(t).

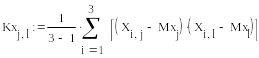
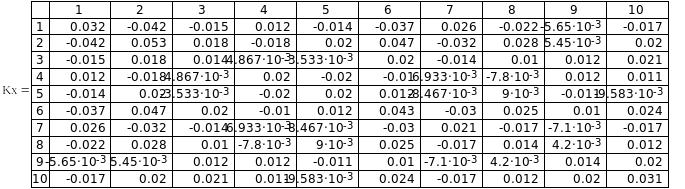
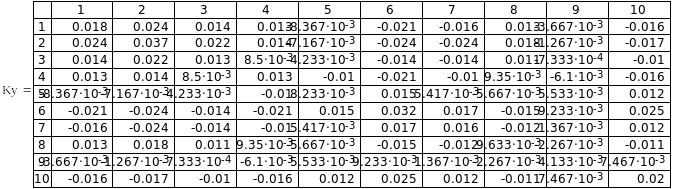
Полученные оценки автокорреляционных функций – симметричные относительно главной диагонали матрицы размером , на главной диагонали которых расположены дисперсии. То основные свойства автокорреляционной функции выполняются. Значит, вычисления были сделаны верно.

4. Вычислим оценку взаимокорреляционной функции СФ X(t) и Y(t)

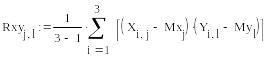
Матрица оценки взаимокорреляционной функции - несимметричная матрица размером , что соответствует общему случаю. Она не является диагональной, т.е. СФ X(t) и Y(t) зависят друга от друга.

5. Построим графики вычисленных оценок.

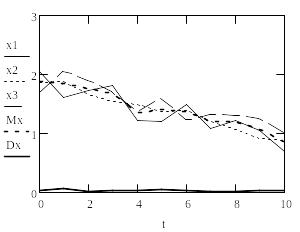
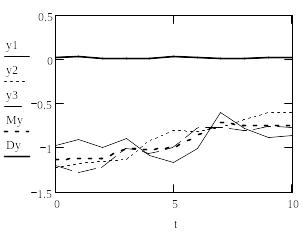
Рис.1. СФ X(t), ее математическое ожидание и дисперсия

Рис.2. СФ Y(t), ее математическое ожидание и дисперсия

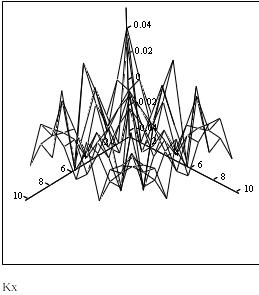
Рис.3. Автокорреляционная функция СФ X(t).

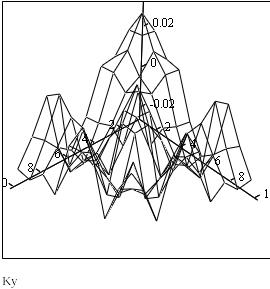
Рис.4. Автокорреляционная функция СФ Y(t).

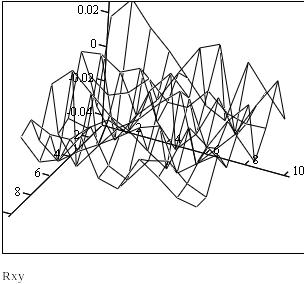
Рис.5. Взаимокорреляционная функция СФ X(t) и Y(t).