4. Метод зейделя

Метод Зейделя представляет собой модификацию МПИ (5) решения СЛАУ, при котором для подсчета i-й компоненты (k+1)-го приближения используются уже найденные на этом, т.е. (k+1)-м шаге, новые значения первых (i-1) компонент. Т.е., если система (1) тем или иным способом сведена к системе (3) с матрицей коэффициентов  и вектором свободных членов , то приближения к ее решению по методу Зейделя определяются системой равенств:

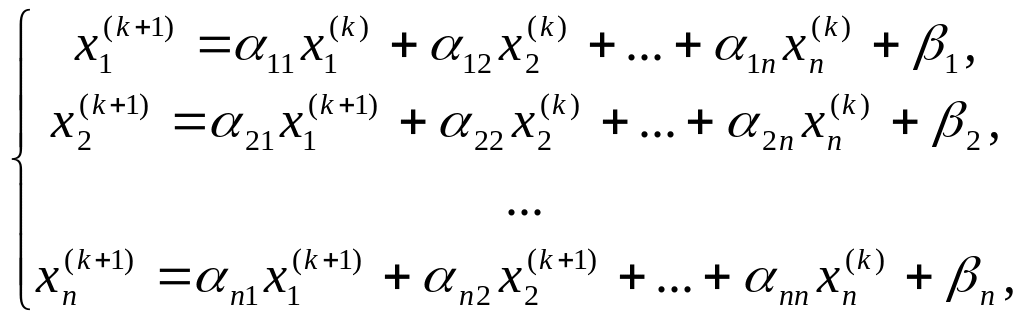(8)

где k = 0, 1, 2, …;

x_i⁽⁰⁾ – компоненты выбранного начального вектора.

Сформулированная выше Теорема 1 о сходимости МПИ остается верной и для метода Зейделя. Выбор начального приближения осуществляется по тому же принципу, что и в МПИ.

Пример 3.

Решим систему примера 2 методом Зейделя.

Итерационный процесс метода Зейделя запишется следующим образом:

х ₁^(k+1) = -0,36х₂^(k) - 0,197х₃^(k) + 2,71

х₂^(k+1) = -0,4х₁^(k+1) + 0,27х₃^(k) + 1,92

х₃^(k+1) = -0,167х₁^(k+1) + 0,208х₂^(k+1) + 2,333,

Начиная процесс вычислений с того же начального приближения x⁽⁰⁾ = 0, последовательно получаем:

х ₁⁽¹⁾ = 2,71

х₂⁽¹⁾ = -0,42,71 + 1,92 = 0,84

х₃⁽¹⁾ = -0,1672,71 + 0,2080,84 + 2,333 = 2,06

х ₁⁽²⁾ = -0,360,84 - 0,192,06 + 2,71 = 2,02

х₂⁽²⁾ = -0,42,02 + 0,272,06 + 1,92 = 1,67

х₃⁽²⁾ = -0,1672,02 + 0,2081,67 + 2,333 = 2,34

х ₁⁽³⁾ = -0,361,67 - 0,1972,34 + 2,71 = 1,65

х₂⁽³⁾ = -0,41,65 + 0,272,34 + 1,92 = 1,89

х₃⁽³⁾ = -0,1671,65 + 0,2081,89 + 2,333 = 2,45

х ₁⁽⁴⁾ = -0,361,89 - 0,1972,45 + 2,71 = 1,54

х₂⁽⁴⁾ = -0,41,54 + 0,272,45 + 1,92 = 1,96

х₃⁽⁴⁾ = -0,1671,54 + 0,2081,96 + 2,333 = 2,48

Истинная ошибка приближения x⁽⁴⁾ метода Зейделя

.

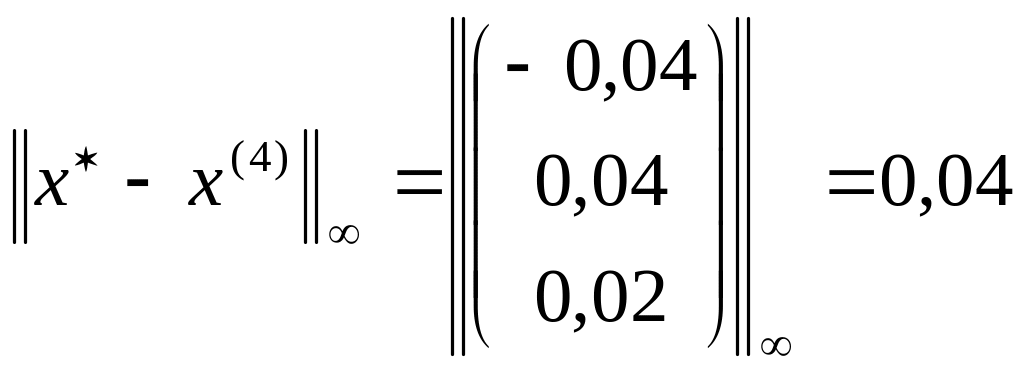Она меньше в 3 раза истинной ошибки метода простых итераций.

Заметим, что обычно метод Зейделя сходится к решению быстрее МПИ.

5. Задание на лабораторную работу

Написать программу, реализующую алгоритмы:

1. метода простых итераций;

2. метода Зейделя.

с точностью  = 10^-12.

В программе требуется:

1. предусмотреть приведение СЛАУ к виду, пригодному для итераций;

2. организовать проверку условия сходимости методов;

3. выбрать начальное приближение;

4. сделать априорную оценку количества шагов и подсчитать реальное количество шагов для достижения заданной точности указанных методов;

5. подсчитать апостериорные оценки методов.

Провести сравнительный анализ метода простых итераций и метода Зейделя.

Варианты заданий на лабораторную работу

1. ; .

2. ; .

3. ; .

4. ; .

5. ; .

6. ; .

7. ; .

8. ; .

9. ; .

10. ; .

11. ; .

12. ; .

13. ; .

14. ; .

15. ; .

16. ; .

17. ; .

18. ; .

19. ; .

20. ; .

21. ; .

22. ; .

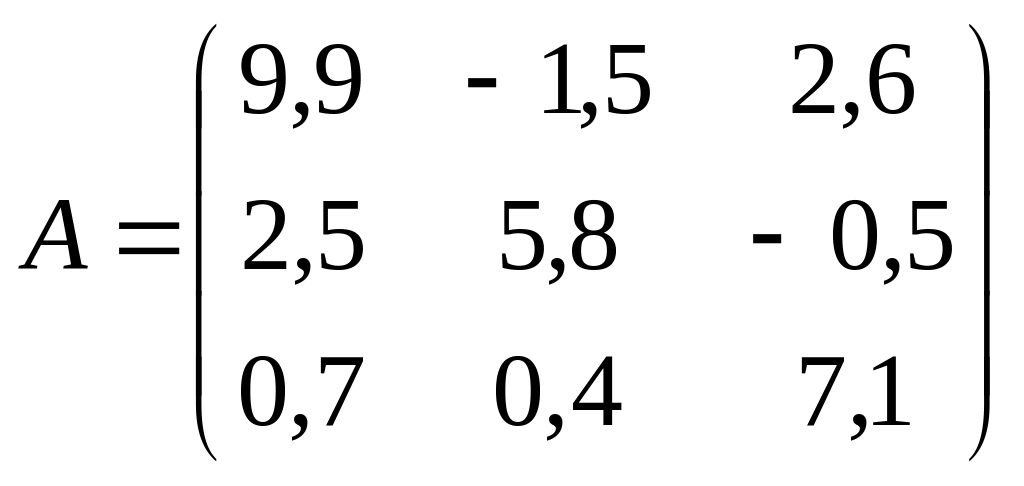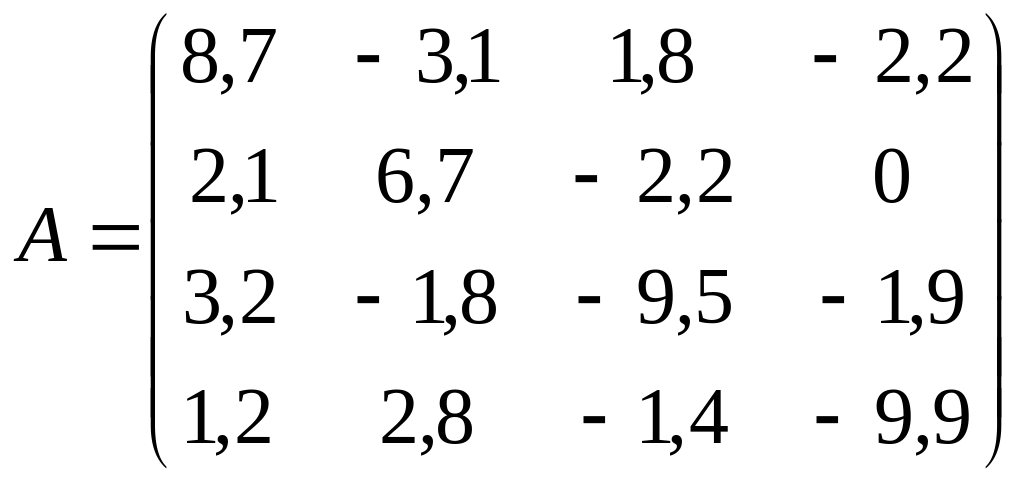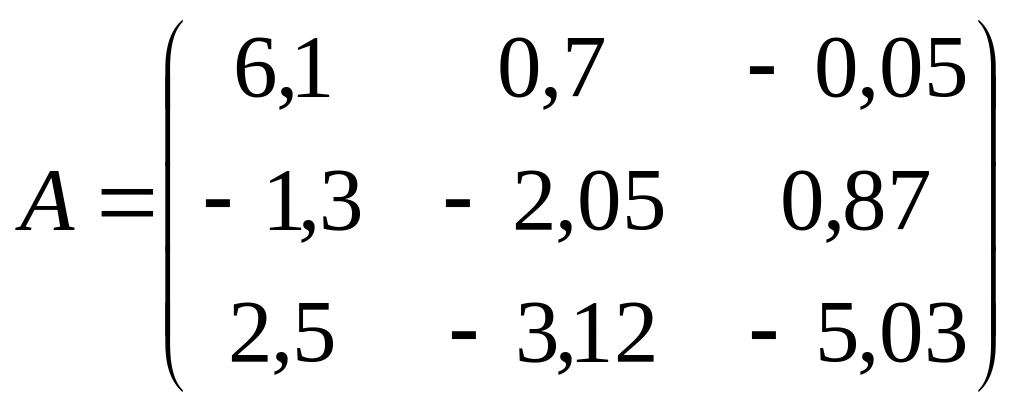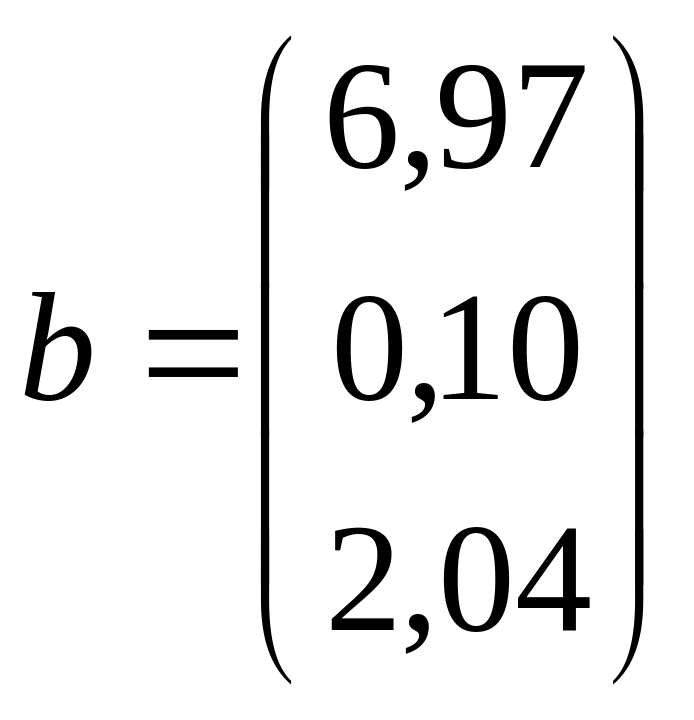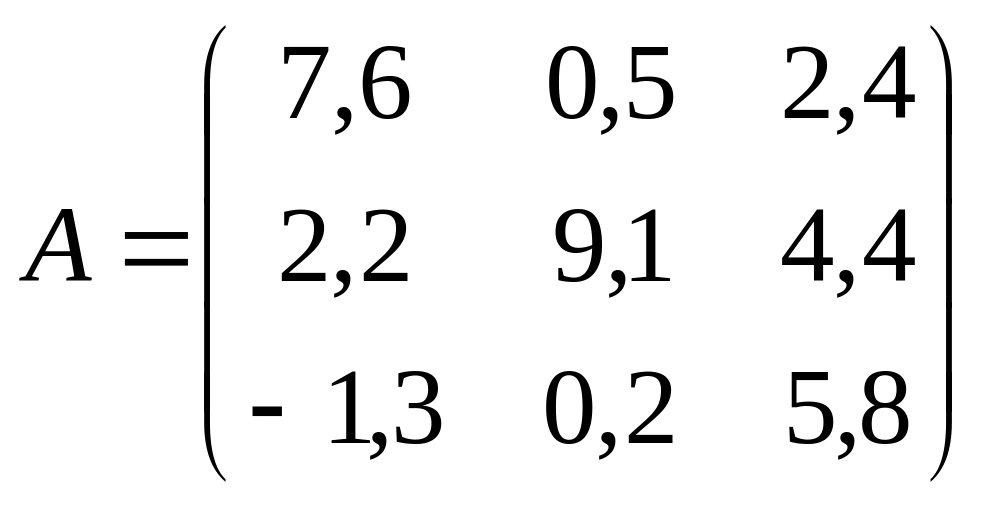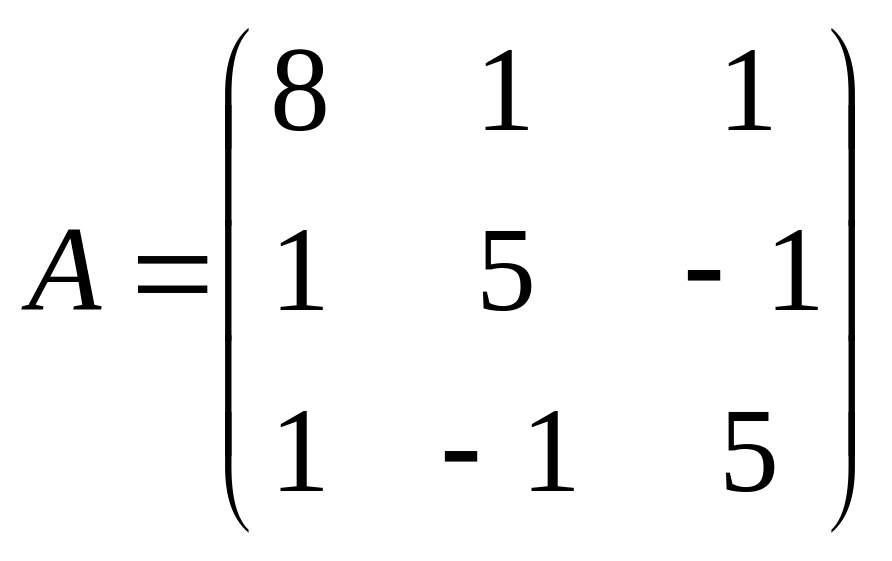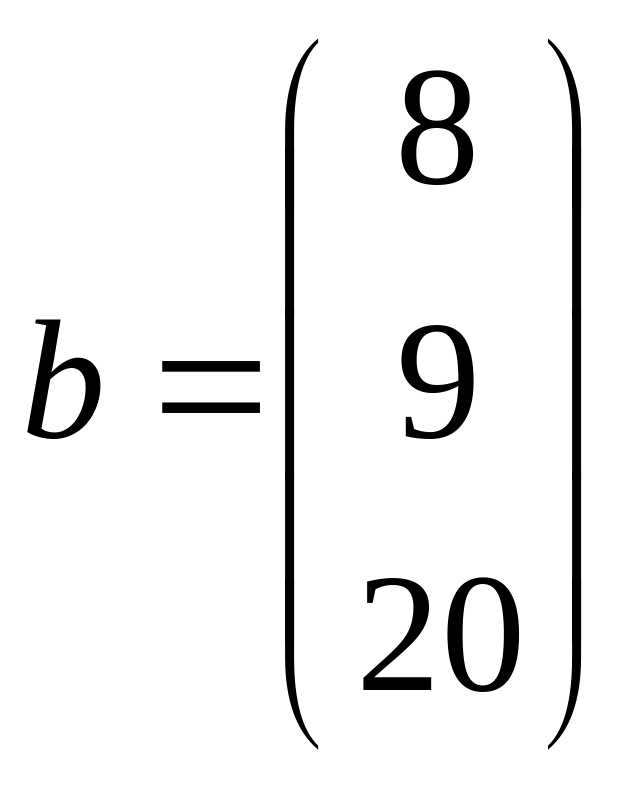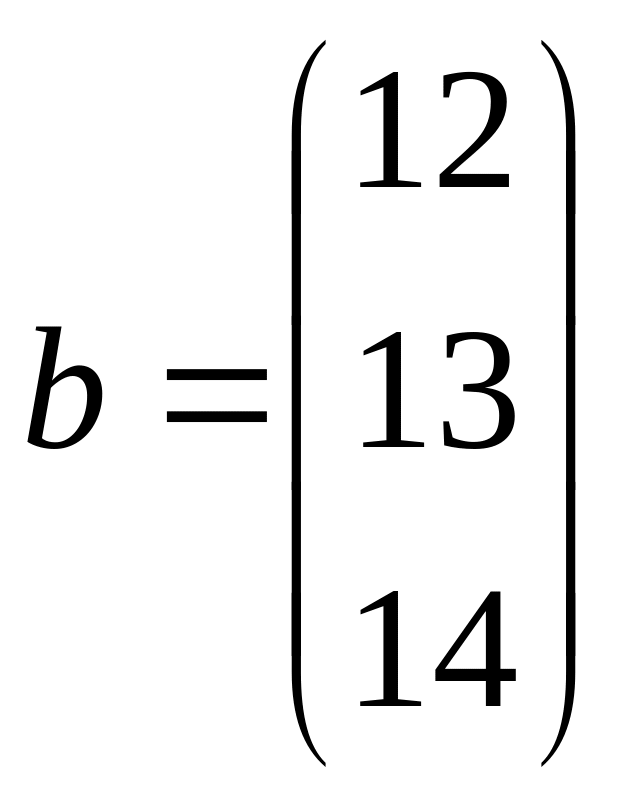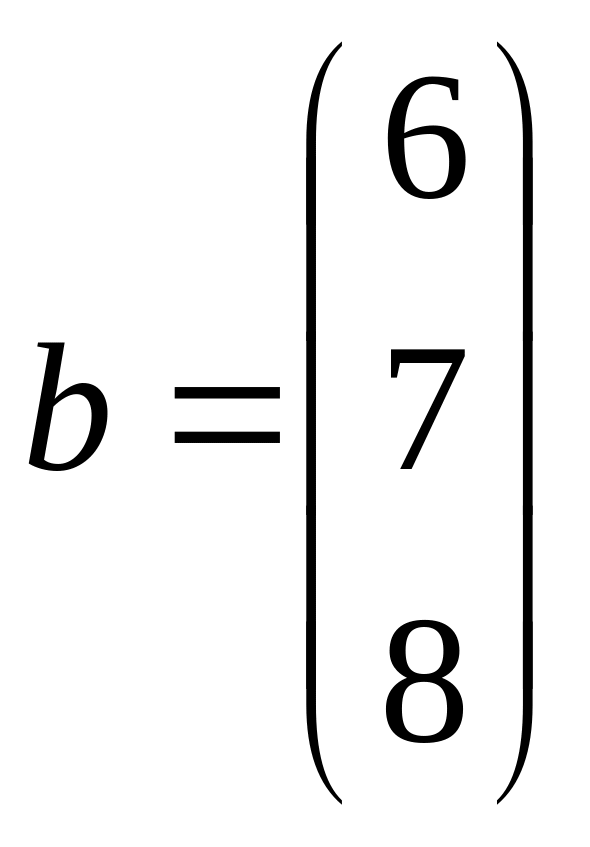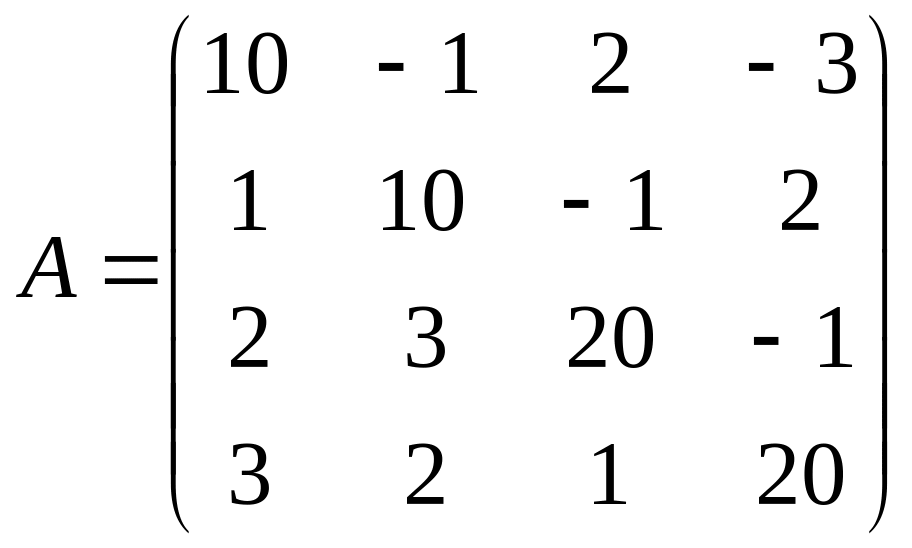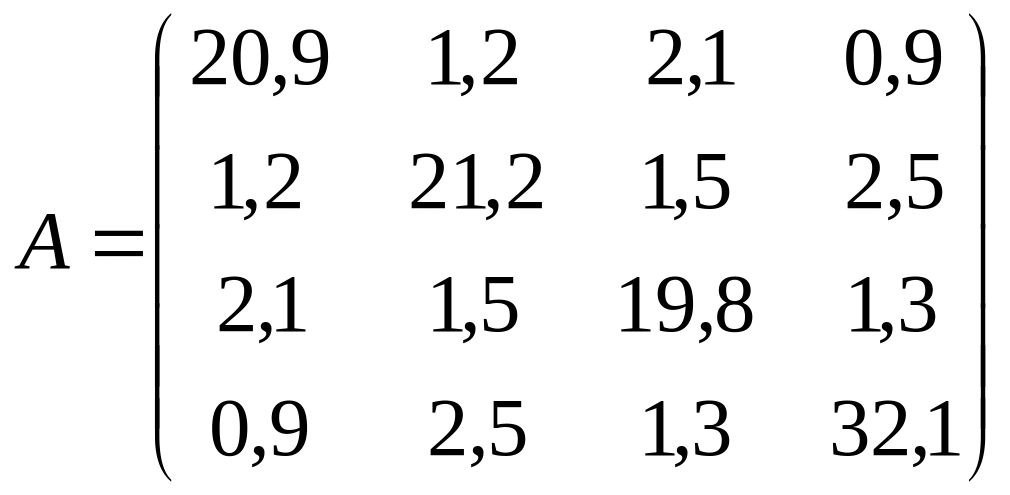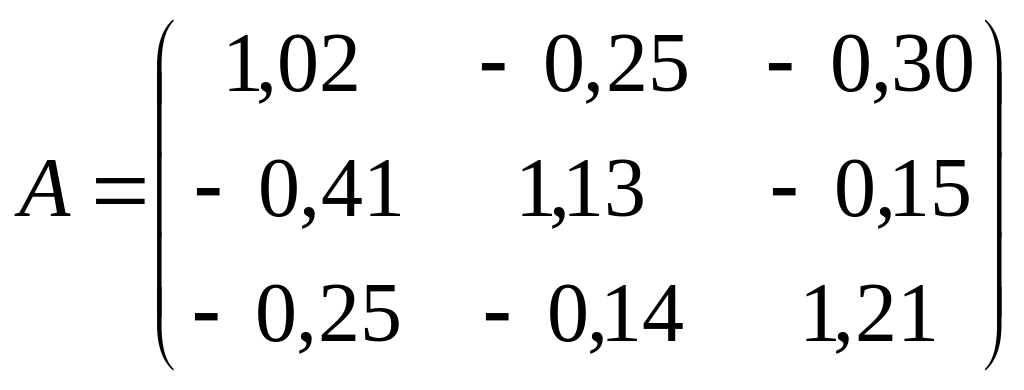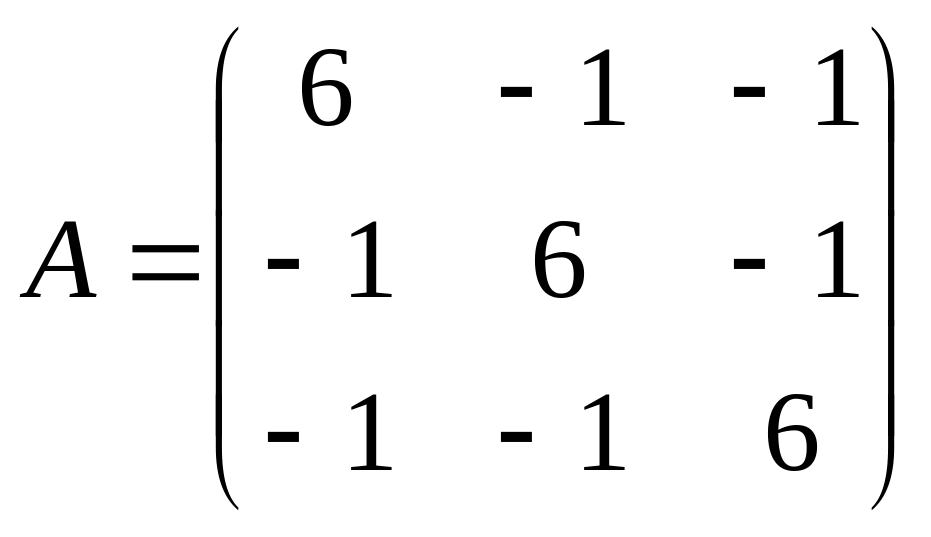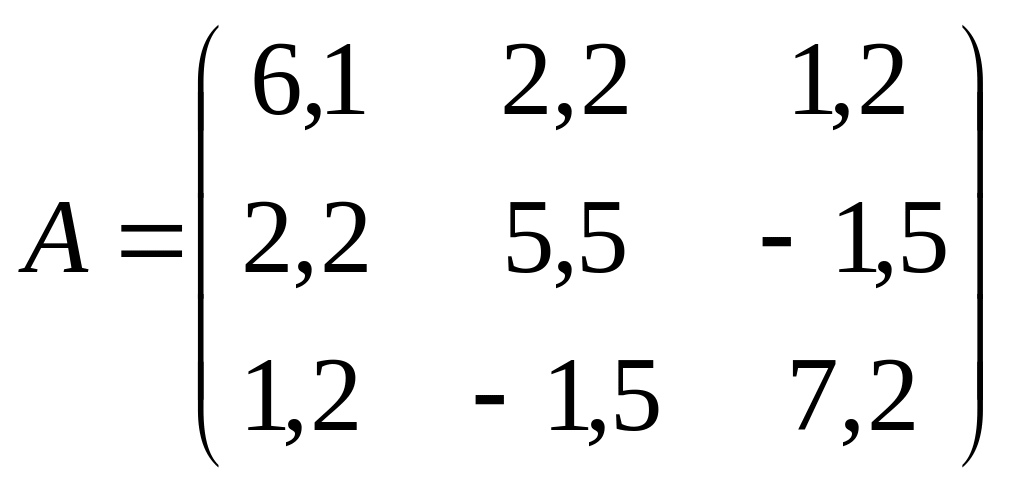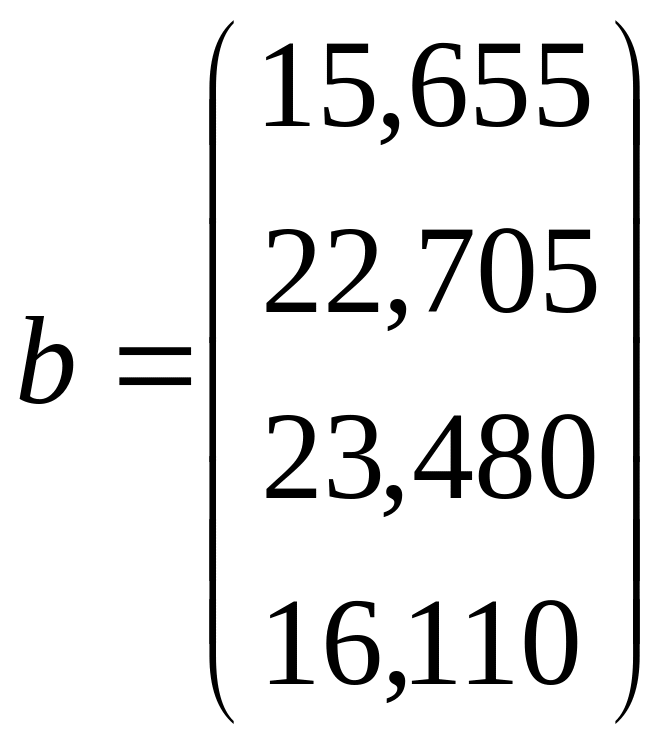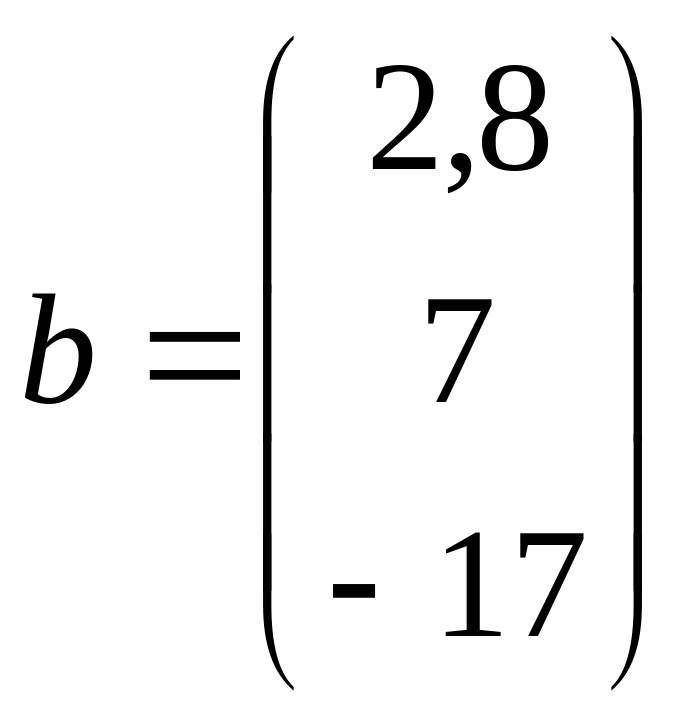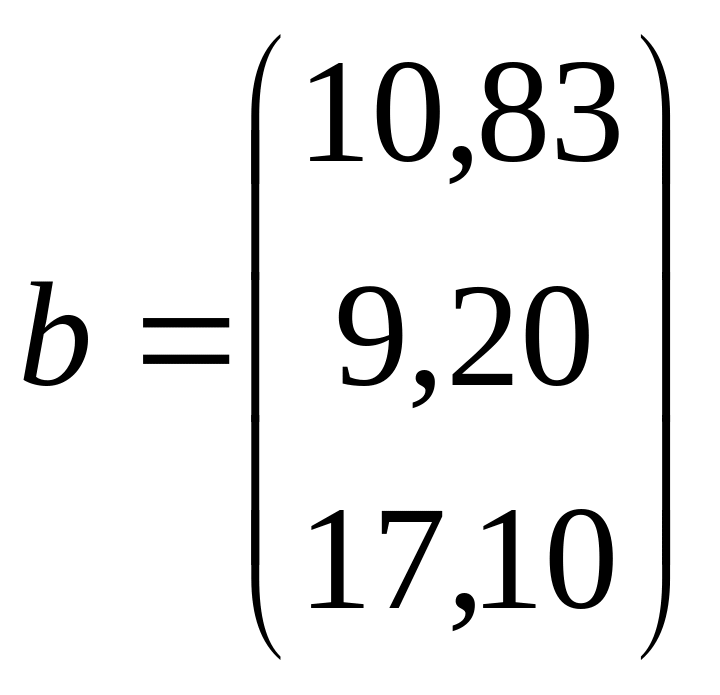6. Содержание отчета по лабораторной работе

В отчете по лабораторной работе должны быть представлены следующие разделы:

1. Постановка задачи.

2. Математическая модель.

3. Текст программы.

4. Результаты работы.

5. Выводы.

Лабораторная работа выполняется на любом языке высокого уровня.

Список литературы

1. Вержбицкий В.М. Основы численных методов. – М.: Высшая школа, 2002.

2. Демидович Б.П., Марон И.А. Основы вычислительной математики. – М.: Наука, 1970.

3. Копченова Н.В., Марон И.А. Вычислительная математика в примерах и задачах. – М.: Наука, 1972.

Пусть дана система n линейных уравнений с n неизвестными:

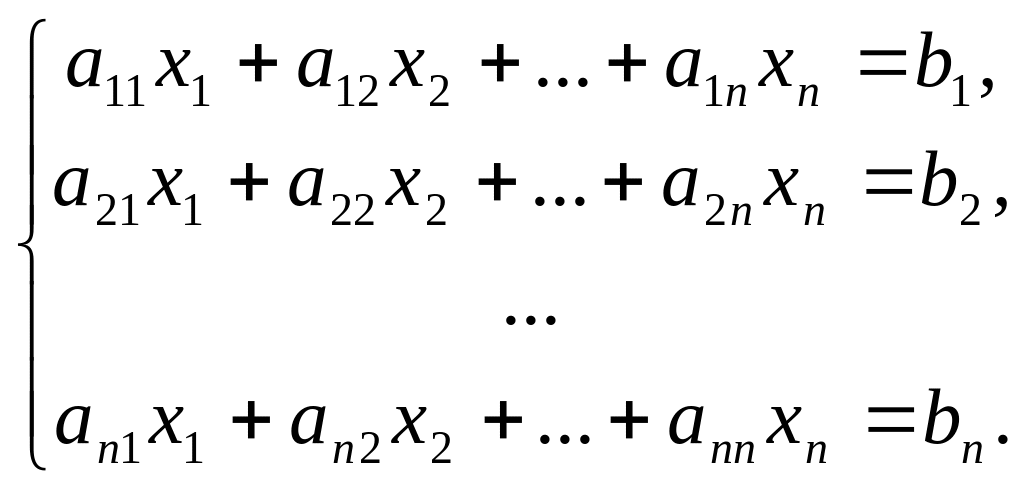(1)

Запишем систему (1) в матричном виде:

A x = b, (2)

Предполагая, что диагональные элементы а_ii  0 (I = 1, 2, …, n), выразим x₁ через первое уравнение системы, x₂ – через второе и т.д. В результате получим систему, эквивалентную системе (1):

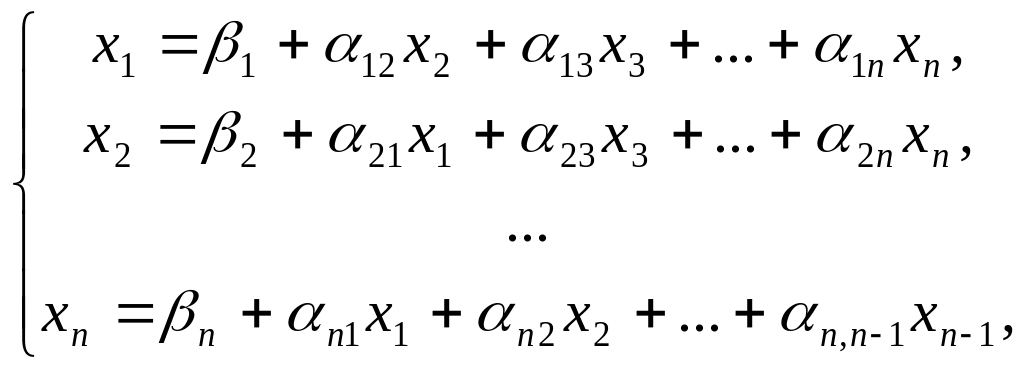(3)

где

; , i = 1, 2, …, n; j = 1, 2, …, n.

Эта система называется приведенной к нормальному виду. Систему (3) запишем в матричном виде:

x = x + . (4)

Решим систему (3) методом простых итераций. За нулевое приближение примем столбец свободных членов:

x⁽⁰⁾ = .

Далее строим приближения

x⁽¹⁾ = x⁽⁰⁾ + ,

x⁽²⁾ = x⁽¹⁾ +  и т.д.

Вообще, любое (k+1)-е приближение вычисляют по формуле:

x^(k+1) = x^(k) + , k = 0, 1, …, n (5)

Если последовательность приближений x⁽⁰⁾, x⁽¹⁾, …, x^(k) имеет предел , то этот предел является решением системы (3), поскольку в силу свойства предела , т.е. x = x + .

Заметим, что иногда выгоднее приводить систему (2) к виду (4) так, чтобы коэффициенты _ii не были равны нулю. Это еще один способ приведения исходной системы (2) к нормальному виду.

Например, уравнение

1,02x₁ – 0,15x₂ = 2,7

для применения метода простых итераций удобно записать в виде:

x₁ = 2,7 – 0,02x₁ + 0,15x₂

19