• методы нелинейного программирования, позволяющие решать задачи, в кото­рых цель описывается нелинейной гладкой функцией, а ограничения задачи - нелиней­ными неравенствами;

• методы стохастического программирования, которыми решаются задачи плани­рования, если все или хотя бы часть параметров являются случайными величинами;

• методы динамического программирования, с помощью которых решаются ли­нейные и нелинейные задачи, представленные в виде пошагового процесса;

• методы целочисленного программирования, с помощью которых решаются за­дачи с условием целочисленности переменных;

• методы выпуклого программирования;

• исследование операций;

• геометрическое программирование и др.

Выбор методов математического программирования для решения оптимизацион­ных задач определяется видом целевой функции f видом ограничений, определяющих область М, и специальными ограничениями на управляемые переменные (например, требованием их целочисленности, неотрицательности и т.д.).

Решением экономико-математической модели, или допустимым планом, называ­ется набор значений неизвестных, который удовлетворяет ее системе ограничений. Мо­дель имеет множество решений, или множество допустимых планов. Среди допустимых планов, удовлетворяющих целевой функции, как правило, имеется единственный план, называемый оптимальным, для которого целевая функция и критерий оптимальности имеют максимальное или минимальное значение. Если модель задачи имеет множество оптимальных планов, то для каждого из них значение целевой функции одинаково.

Если экономико-математическая модель задачи линейна, то оптимальный план достигается в крайней точке области изменения переменных величин системы ограни­чений. В случае нелинейной модели оптимальных планов и оптимальных значений це­левой функции может быть несколько. Поэтому необходимо определять экстремальные планы и экстремальные значения целевой функции. План, для которого целевая функ­ция модели имеет экстремальное значение, называют экстремальным планом, или экс­тремальным решением.

Таким образом, для принятия оптимального решения любой экономической зада­чи необходимо построить ее экономико-математическую модель, по структуре вклю­чающую в себе систему ограничений, целевую функцию, критерий оптимальности и решение (оптимальный план).

2. Методика построения оптимизационной модели

Методика построения оптимизационной модели состоит в том, чтобы экономи­ческую сущность задачи представить математически, используя различные символы, переменные и постоянные величины, индексы и другие обозначения.

Все условия задачи необходимо записать в виде уравнений или неравенств. По­этому, в первую очередь необходимо определить систему переменных величин, которые могут для конкретной задачи обозначить искомый объем производства продукции на предприятии, количество перевозимого груза поставщиками конкретным потребителям и т. д. Как правило, для обозначения переменных величин используются буквы: х, у, z, а также их модификации. Например, модификация переменной х: х, х, х^,х', х_(; и т. д. Ана­логичные модификации могут быть и для других переменных, используемых в модели. Переменные Xj, х₂, ..., х„ могут обозначать объемы производства или реализации про-

14

дукттии соответственно первого, второго и так далее и-го вида. Переменные х_и- могут обозначать объемы производства продукции /-го вида j-м технологическим способом. Для индексации, как правило, используются латинские буквы: /, j, s, I Количество пере­менных может обозначаться буквами п, к, т. По каждой переменной для конкретной за­дачи дается словесное пояснение.

Целевую функцию (цель задачи) чаще всего обозначают буквами f F, Z. Постоян­ные величины обычно обозначают буквами: а, Ь, с, d и т. д.

Ограничения модели должны отражать все условия, формирующие оптимальный план. Однако практически учесть все условия задачи для достижения цели невозможно, достаточно учесть основные условия. Естественно, полученная модель будет упрощен­ной по сравнению с реальной, которая отражала бы все условия поставленной задачи.

Итак, в упрощенном виде экономико-математическая модель представляет собой:

1. систему ограничений - равенства, неравенства вида больше или равно (>), меньше или равно (<);

2. условия неотрицательности переменных, исходя из экономической или физи­ческой сущности переменных (pcj > 0),и = Ъ»У,

3. целевую функцию.

Математически общую модель задачи можно представить в виде:

найти значения п переменных Xj, х₂, ..., х„, которые удовлетворяют системе огра­ничений

f (х_ь х₂, ..., х„) {< = >} b_t(i = 1, т) (2.2)

и максимизируют или минимизируют целевую функцию

Z =/(х /, Л'7, ..., х„) —> (т ах/т in). (2.3)

Если на переменные налагается условие неотрицательности, тогда в модель зада­чи вводится условие

(Xj >0), (j = U0- (2.4)

Иногда на переменные налагается условие целочисленности, тогда его можно за­писать в виде

Xj = 0, или 1, или 2, или 3 и т. д.

3. Основные типы линейных экономико-математических моделей

Среди линейных моделей математического программирования особое место за­нимают четыре типа моделей:

1. модель общей задачи линейного программирования;

2. модель транспортной задачи линейного программирования;

3. модель распределительной задачи линейного программирования;

4. модель ассортиментной задачи линейного программирования.

1. Модель общей задачи линейного программирования применяют для решения за­дач планирования в торговле, использования сырья, определения оптимального плана выпуска изделий и др.

15

В торговле планирование связано с поиском наиболее выгодного варианта рас- пределения различного вида ресурсов: финансовых, трудовых, товарных, материальных, технических и др. Модель общей задачи линейного программирования применяют для решения широкого круга задач торговой практики, таких как планирование товарообо- рота; организация рациональных закупок продуктов питания (задача о диете); замена торгового оборудования; определение ассортимента товаров для торговой базы в силу ограниченной площади хранения; установление рационального режима работы и т.д.

1. Модель оптимального планирования товарооборота. Торговое предприятие реализует товары нескольких групп: А, В, С. Для реализации единицы товара группы А затраты рабочего времени составляют а_п чел.-ч., товара группы В - а ₁₂ чел.-ч., товара группы С - a is чел.-ч. Площадь торгового зала, занимаемая единицей товара А, состав- ляет a₂i м², товара В - а₂₂ м², товара С - а₂₃ м². Расходы (издержки обращения) при про- даже единицы товара группы А составляют а₃₁ ден. ед., группы В - а₃₂ ден. ед., группы С - а_Зз ден. ед. Известны величины ресурсов: рабочее время - bj чел.-час., площадь тор- гового зала Ь₂ м², издержки обращения Ь₃ ден.ед. Доход при реализации единицы товара группы А равен с/ ден. ед., товара группы В - с₂ ден. ед., товара группы С - с₃ ден. ед.

Требуется составить экономико-математическую модель задачи, пользуясь кото- рой, можно найти план товарооборота по критерию максимума дохода/

Экономико-математическая постановка задачи. Известно, что величина дохода линейно связана с объемом продажи товаров Xj, х? и х₃. В связи с этим целевую функ- цию можно записать таким образом:

/= (cj X/ + с₂ х₂ + с₃ х₃) —> max. (2.5)

Очевидно, что объем продажи товаров не может быть отрицательной величиной. Поэтому Xj > 0, х? > 0, х₃ > 0. Учитывая нормы затрат рабочего времени и то, что общие затраты в целом не должны превышать имеющихся ресурсов, запишем следующее огра- ничение:

«11 А +^12^2 +ЯгА —^Г (2 6)

Исходя из торговой площади и общей площади запишем следующее ограничение:

ci_2l б₁ + й₂₂ б₂ + й_2Ъ о₃ < Ъ₂. ^2 7)

Поскольку известны ограничения по издержкам обращения, запишем последнее ограничение

а^х, +а^х^ +а„х, <Г

'31^Л1 ¹ “32^л2 ¹ “33^л3 — ^3-

(2.8)

2. Модель планирования рациональных покупок продуктов питания (задача о диете). Нередко возникают задачи, связанные с осуществлением рациональных покупок продовольственных товаров, обеспечивающих необходимый рацион питания. Задачи о рациональном питании решаются в условиях ограниченного ассортимента, товарных за­пасов, стоимости, суточных норм потребления питательных веществ и их содержания в продуктах. В любом случае из всех возможных вариантов необходимо выбрать самый экономичный.

16

Экономико-математическая постановка задачи. Допустим, имеется набор про­дуктов: мясо, рыба, молоко, сахар, яйца, картофель, овощи, фрукты, хлеб, мука по цене соответственно: c_h , с„, причем запасы этих продуктов ограничены: a_lt ..., а„.

Содержание питательных веществ - белков, жиров, углеводов, витаминов и ми­неральных солей - в 1 кг каждого продукта известно и составляет соответственно: qu, Я21, • ••> ^clih • ••> Яти- Кроме того, известны нормы суточной потребности человека в каж­дом питательном веществе: b_t, b₂, ..., Ь_т.

Перечисленные показатели можно записать в виде системы линейных ограниче­ний:

q_nx_x + q_l2x₂ +... + q_XjXj +... + q_lnx„ > b_u q_2lx_l+q₂₂x₂+... + q_2jx_j +... + q_2nx_n > b₂,

< ’ (2.9)

q_nx_x + q_n2x₂ +... + q_i]X] +... + q_mx_n > b,,

_ + ^Cl_m2*2 + - + Ящ-Xj +- + ^Clnm^Xn > ^Ьпг

Еще одно ограничение связано с тем, что количество каждого продукта в рационе, с одной стороны, не может быть величиной отрицательной, а с другой — его покупка ограничена запасами:

0<Xj<aj, 0 < х₂ < а₂,...,0 < Xj < ctj. (2.10)

В задаче необходимо определить такое количество закупаемых продуктов, кото­рое бы обеспечило потребность человека в питательных веществах при минимальной стоимости набора и описывалось бы линейной формой связи целевой функции:

у = [cjXj + с₂х₂ +... + CjXj +... + с_пх_пmin . (2.11)

3. Модели рационального распределения материальных ресурсов. В общем виде данная задача может быть сформулирована следующим образом:

а) имеется т видов исходных материальных ресурсов, объемы которых ограниче­ны определенной величиной ai = I, 2 т;

б) из этих ресурсов необходимо изготовить п видов продукции, при этом мини­мальный объем выпуска продукции каждого вида bj задан в производственном плане; j = I 2,..., п;

в) заданы нормы расхода ресурса /-го вида на выпуск единицы /-ой продукции а у, которые принимаются постоянными, не зависящими от объема выпуска продукции:

г) известна прибыль, получаемая при реализации единицы /-го вида продукции, с,- (или себестоимость изготовления этой единицы sj, эти величины также принимаются не зависящими от объемов выпуска.

Требуется составить такой план распределения исходных материальных ресурсов, чтобы сумма прибыли от реализации всей продукции была максимальной (или общая себестоимость изготовленной продукции была минимальной).

Экономико-математическая постановка задачи. Обозначим через х₇ количество продукции /-го вида, которое следует изготовить в целях удовлетворения выбранного критерия оптимальности. Требуется определить множество неотрицательных перемен­ных Ху _ 0, где j = 1,2,..., w, удовлетворяющих ограничениям по ресурсам

17

б, > Ъл / = 1,77.

(2.13)

При этом целевая функция имеет вид

• для прибыли

• для себестоимости

(2.14)

(2.15)

4. Модели оптимального составления смесей. В ряде производств готовая продукция получается путем смешивания различных исходных компонентов, при этом качество готовой продукции должно соответствовать определенным требованиям при достижении максимального экономического эффекта. Оптимизация состава исходных компонентов представляет собой экономико-математическую задачу, которая на­зывается задачей о смесях.

В общем виде задача о смесях может быть сформулирована следующим образом. Состав готовой продукции определяется содержанием в нем т видов элементов, содер­жание которых лимитируется величиной l_t (i = 1, 2 т). Для к элементов, ухудшаю­щих качество продукции, задана верхняя граница содержания того или иного элемента (/, < a_j), а для (т - к) элементов, улучшающих качество продукции, задана нижняя гра­ница содержания элемента в готовой продукции (1. > а₁). Для производства готовой про­дукции может быть использовано п видов компонентов, объемы которых ограничены величиной bj (j = 1,2 п). Известно содержание /-го элемента в /-ом компоненте, кото­рое обозначим как a_tj. Известна стоимость отдельных компонентов, включая расходы на их переработку, которую обозначим как с,-. Наконец, задано общее количество М гото­вой продукции, которое следует изготовить по плану. Требуется составить такую смесь из имеющихся компонентов, чтобы затраты на это составление были минимальными.

Экономико-математическая постановка задачи. Обозначим количество исполь­зуемого для составления смеси /-го компонента через Х/, вектор, координатами которого являются величины Xj, обозначим через X. Целевая функция задачи имеет вид

(2.16)

а ограничения формируются следующим образом:

п

(2.17)

п

(2.18)

18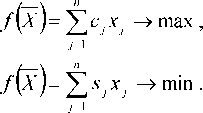

2>, =м-

(2.19)

(2.20)

Ограничения (2.17) относятся к элементам, ухудшающим качество; (2.18) - к эле­ментам, улучшающим качество; (2.19) - по плану производства; (2.20) - по ограничению ресурсов.

5. Задача о рангов (или о рюкзаке). Так называется задача о наилучшем выборе предметов из общего их количества таким образом, чтобы суммарный вес (или габариты) отобранных предметов не превышал заданной величины, а их суммарная полезность или иная общая оценка (количество калорий, общая стоимость и т. д.) была максимальной. Задача о ранце решается как задача целочисленного линейного программирования, мето­дами динамического программирования и другими методами. В частности, эта задача применяется при планировании оптимальной загрузки складов и др.

1. Модель транспортной задачи линейного программирования. Сущность транс­портной задачи линейного программирования состоит в наивыгоднейшем прикреплении поставщиков однородного продукта ко многим потребителям этого продукта. На прак­тике постоянно возникает необходимость решения таких задач, особенно когда количе­ство пунктов отправления и получения грузов увеличивается.

Модель транспортной задачи линейного программирования может использовать­ся для планирования ряда операций, не связанных с перевозкой грузов. Так, с ее помо­щью решаются задачи по оптимизации размещения производства, топливно- энергетического баланса, планов загрузки оборудования, распределения сельскохозяй­ственных культур по участкам различного плодородия и т.п.

В торговле модель транспортной задачи линейного программирования применя­ется для решения следующих задач: планирование товароснабжения города, района; прикрепление торговых предприятий к поставщикам; организация рациональных пере­возок товаров из пунктов отправления (баз, станций, фабрик, совхозов, заводов) в пунк­ты назначения (магазины, склады); распределение работников торговли по должностям (задача о назначении); планирование капиталовложений; оптимизация межотраслевых связей торговли; размещение розничной торговой сети города и т.д.

Условие транспортной задачи обычно записывается в виде матрицы, в которой потребители однородного груза размещаются по столбцам, а поставщики - по строкам. В последнем столбце матрицы проставляют запас груза, имеющийся у каждого постав­щика, а в последней строке - потребность в нем потребителей. На пересечении строк со столбцами (в клетках матрицы) записывают размер поставки, а также расстояние пробе­га по всем возможным маршрутам, время доставки груза или затраты на перевозку еди­ницы груза по этим маршрутам.

Математически транспортная задача по критерию стоимости формируется сле­дующим образом.

2. 1 Статическая модель оптимизации прикрепления потребителей к поставщи­кам. В т пунктах отправления А /, А₂ А_т, которые в дальнейшем будем называть по-

19

ставщиками, сосредоточено определенное количество единиц некоторого однородного продукта, которое обозначим a_t (i = 1, 2 т).

Данный продукт потребляется в п пунктах В/, В₂ В„, которые будем называть

потребителями; объем потребления обозначим bj(j = 1,2, , п).

Известны расходы на перевозку единицы продукта из пункта А, в пункт Bj, кото­рые равны Су и приведены в матрице транспортных расходов С = (с у).

Требуется составить такой план прикрепления потребителей к поставщикам, дру­гими словами, план перевозок, при котором весь продукт вывозится из пунктов А, в пункты Bj в соответствии с потребностью и общая величина транспортных издержек минимальна.

Экономико-математическая постановка задачи. Обозначим количество продук­та, перевозимого из пункта А, в пункт Bj через х,_г Совокупность всех переменных Ху для краткости обозначим символом X, тогда целевая функция задачи приобретет вид

/ \ т п

/(^Л ) ZZ^{r х min} ’ (²-²¹)

'■=1 У=1

а ограничения выглядят следующим образом:

т

Z^{v h}'-i ^L"^; (²-²²)

i=l

=a_i-,i = l,m; (2.23)

^xv - 0 • (2.24)

Условия (2.22) означают полное удовлетворение спроса во всех пунктах потреб­ления; условия (2.23) определяют полный вывоз продукции от всех поставщиков.

Необходимым и достаточным условием разрешимости задачи (2.21-2.24) является условие баланса

т п

(2.25)

'=1 У=1

Транспортная задача, в которой имеет место равенство (2.25), называется закры­той и может быть решена как задача линейного программирования.

2. Модель оптимизации загрузки производственных мощностей. В общем виде эту задачу можно сформулировать следующим образом.

Имеется т предприятий (например, филиалов фирмы), которые могут произво­дить п видов продукции. Известны:

а) а, - фонд рабочего времени (например, в сменах) каждого /-го предприятия; / = 1, 2 т;

б) bj - величина потребности в продукции /-го вида; j = 1, 2 п;

в) ау - мощность, или количество продукции /-го вида, вырабатываемой (в смену) на /-ом предприятии;

г) с у - себестоимость производства единицы /-ой продукции на /-ом предприятии.

Требуется составить такой план распределения заказов на продукцию по всем

предприятиям, при котором суммарные затраты по изготовлению продукции в заданной

20

номенклатуре будут минимальными при полной загрузке производственных мощностей предприятий.

Экономико-математическая постановка задачи. Пусть Ху - планируемый объем выпуска /-ой продукции на /-ом предприятии; совокупность таких величин обозначим

О . Тогда целевая функция рассматриваемой задачи имеет вид

/ \ т п

f\^x)= ZZ^{r х} ->^min (²-²⁶)

'■=1 у=1

при ограничениях

• —= а;/ = 1, да; (2.27)

;=1 “а

т

Z" ^b'-i ^L"^; (²-²⁸)

i=1

^ху - 0 • (2.29)

Если снять условие полной загрузки производственных мощностей предприятий, то ограничения (2.27) примут вид неравенств

(2.30)

если условие точного выполнения плана в заданной номенклатуре заменить требовани­ем «не меньше», то условия (2.28) превратятся в неравенства

Очевидно, задачу (2.26) - (2.29) можно решить как задачу линейного программи­рования. Однако если привести определенными приемами коэффициент ау к единице, то данная модель не будет отличаться от модели транспортной задачи.

2. Модель рационального распределения работников по должностям (задача о назначении). В сфере торговли и общественного питания часто возникают задачи, свя­занные с рациональным распределением работников или механизмов по отдельным ви­дам работ. Известно, что один и тот же работник может выполнить различные функции с разной производительностью в зависимости от опыта работы, квалификации, индиви­дуальных особенностей. Поэтому возникает задача о назначениях, предполагающая та­кое распределение работников, при котором производительность труда в коллективе была бы максимальной.

Приведем следующий пример. В универмаге имеется п работников: А /, А₂ A_t,

, А,„ каждый из которых может выполнять одну Bj из имеющихся п видов работ: В/, В₂ Bj, ..., В„.

Для каждого работника A_t на любом рабочем месте Bj известна производитель­ность труда а у. Полагаем, что если работник назначен на работу Bj, то переменная на­значения Ху = 1, или Ху = 0, если он на эту работу не назначен, что можно записать так

21