
- •Экономико-математические методы и модели
- •Содержание
- •Объекты изучения и методы исследования курса «Экономико-математические методы и модели».
- •Понятие экономико-математической модели и моделирования
- •Классификация экономико-математических моделей
- •Основные этапы экономико-математического моделирования
- •Программное обеспечение экономико-математического моделирования
- •Методика построения оптимизационной модели
- •Основные типы линейных экономико-математических моделей
- •1, Апеё а 'шдоддд адШёо iddddga ёс didiad I a didid j,
- •Основные инструменты анализа экономических данных1
- •Применение корреляционного анализа для решения экономических задач1
- •Применение регрессионного анализа для решения экономических задач1
- •Трендовые модели прогнозирования экономических процессов
- •Модели управления однономенклатурными запасами.
- •Модели управления многономенклатурными запасами.
- •Основные понятия экономико-математических моделей управления запасами
- •Модели управления однономенклатурными запасами1
- •Модели управления многономенклатурными запасами1
- •Основные характеристики смо1
- •Классификация смо
- •Смешанного типа
- •С параллельными каналами
- •Экономико-математическая постановка задач массового обслуживания
- •Основные понятия, определения и графические обозначения спу
- •Правила построения сетевых графиков
- •Основные параметры сетевых моделей и методы их расчета
- •Постановка задач для решения методами спу
- •Виды и сущность оптимизации сетевых моделей
- •Матричные игры с нулевой суммой
- •Решение матричных игр в чистых стратегиях
- •Решение матричных игр в смешанных стратегиях
- •Решение статистических игр по различным критериям
- •Общие понятия балансового метода.
- •Экономико-математическая модель межотраслевого баланса.
- •Общие понятия балансового метода
- •Принципиальная схема межотраслевого баланса
- •Экономико-математическая модель межотраслевого баланса
Рисунок
6.2 - Различие событий по признакам
входящих и выходящих работ
Если
в событие а
входит и выходит из него только одна
работа, то такое событие является
простым.
Если в событие б
входят две или более работы, то такое
событие называется сложным
событием на входе.
Если из события в
выходят две или более работы, то
такое событие является сложным
событием на выходе.
Событие г, в которое входят и из которого
выходят по две и более работы, считается
сложным.
Приведенные
выше характеристики событий являются
существенными при расчете их
параметров.
В
отличие от работы событие не является
процессом и не имеет продолжительности
во времени. Оно означает момент времени,
к которому завершено выполнение
последней из входящих в него работ,
и возможность приступить к выполнению
непосредственно следующих за ним
работ. Событие не может свершиться,
пока не будут выполнены все
непосредственно предшествующие ему
работы, т. е. свершается в логической
последовательности, обусловленной
технологией процесса.
Таким
образом, событие имеет двойственное
значение: с одной стороны, оно означает
факт состоявшегося выполнения
непосредственно входящих в него работ,
и с другой — свидетельствует о возможности
приступить к выполнению непосредственно
следующих за ним работ. Двойственное
значение события состоит также и в том,
что для всех непосредственно предшествующих
ему работ оно является конечным,
а для всех непосредственно следующих
за ним — начальным.
Так, событие 6
на рисунке 6.1 для работы (6,7) является
начальным, а для работы (5,6) конечным.
Кроме
событий, имеющих двойственное значение,
в сетевой график всегда входят особые
события: исходное и завершающее.
Исходное
событие
означает наличие условий для начала
выполнения всего комплекса работ.
Оно не имеет в рамках рассматриваемой
сети предшествующих работ, так как не
является результатом ни одной из работ
данной сети. Исходное событие определяет
совокупность условий, необходимых для
того, чтобы головной исполнитель мог
приступить к выполнению комплекса
работ.
Завершающее
событие
означает факт, свидетельствующий о
том, что конечная цель всего комплекса
операций достигнута. Завершающее
событие не имеет следующих за ним работ,
включенных в рассматриваемый комплекс
операций, поскольку оно не является
условием начала ни для одной из работ,
входящих в данную сеть.
Любая
работа сетевой модели соединяет два
события: начальное событие работы и
конечное событие работы. Для однозначного
обозначения работ используют
идентификаторы (i,
j),
где / — номер начального события работы,
у — номер конечного события работы.
Обычно на сетевых графиках события
упорядочены, то есть / < j.
55
Правила построения сетевых графиков
Каждая
работа должна иметь определение,
означающее ее содержание (например,
составление сметы, подбор кадров, монтаж
оборудования, выкладка товаров и т.
д.). Наименование (содержание) работы
указывают под стрелкой, а продолжительность
— над стрелкой. Всем стрелкам сетевого
графика задают общее направление слева
направо. События нумеруют последовательно
слева направо и сверху вниз.
При
построении сетевых графиков соблюдают
следующие правила:
между
каждыми двумя событиями может быть
изображена только одна работа.
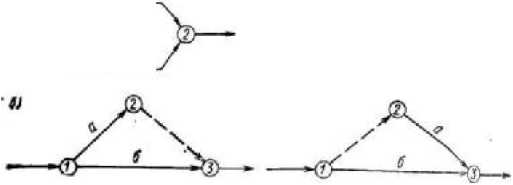
Параллельно выполняемые работы нельзя
изображать через их общее начальное
и конечное событие. Для их правильного
изображения вводят дополнительные
события и зависимости (рисунок 6.3);
Рисунок
6.3 - Построение параллельно выполняемых
работ: а — неправильно; б — правильно
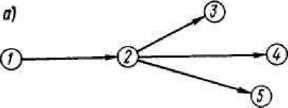
если
какие-либо работы в сети, например,
работы (2,3) и (2,4) (рисунок 6.4), могут быть
начаты до полного окончания непосредственно
предшествующей им работы
,
то последняя (работа (1,2))
может быть выражена как сумма отдельных
ее частей (1,2а)
и (2а,
26), выполнение которых необходимо и
достаточно для начала следующих за
ними работ. После выполнения работы
(1,2а) можно начать работу (2а, 3), после
(2а, 26) - работу (26, 4) и т.д.;
Рисунок
6.4 - Разделение работы (1,2) на части,
необходимые и достаточные для начала
работ
(2а, 3); (26, 4); (26, 5): а
— работы (2,3), (2,4), (2,5) ждут полного
окончания работы (1,2); б
— работы (2,3), (2,4) могут быть начаты, не
ожидая окончания всей работы (1,2)
в
сетевом графике для отражения
взаимосвязей между работами применяют
зависимости (фиктивные работы). Так,
например, фиктивная работа (6,7) (см
рисунок 6.1) означает, что возможность
начала работ (7,8) зависит не только от
выполнения работы (6,7), но и от работы
(5,6);
в
сетевом графике нельзя допускать
«замкнутых контуров» (циклов), т. е.
путей, состоящих из работ, направление
стрелок которых создает замкнутую
цепь, как это показано на рисунке 6.5.
Наличие замкнутых контуров свидетельствует
об ошибках или при построении сетевого
графика, или при составлении исходных
данных и исключает возможность правильно
выполнять расчет параметров сетевого
графика;
56

Рисунок
6.5 - Примеры недопустимых замкнутых
контуров: а
— замкнутые контуры 4-5-6-7-4; 4-5-7-4; б
— замкнутый контур 5-6-7-5.
в
сетевом графике нельзя допускать
«тупиков» т. е. событий, кроме
завершающего, из которых не выходит
ни одной работы, например событие 4
(рисунок 6.6).
Наличие «тупиков» показывает, что
не выявлены полностью взаимосвязи или
в графике показаны излишние работы,
которые фактически не влияют на
достижение конечной цели;
в
сети не должно быть событий, за
исключением исходного, в которые не
входит ни одна работа, например
событие 6
(рисунок 6.6).
Разработка
сети всегда проводится без учета
масштаба времени составляющих его
работ. Поэтому длина стрелки-работы в
каждом отдельном случае зависит только
от необходимости обеспечить простую
и четкую структуру сетевого графика и
разместить соответствующие показатели
на каждой работе. Как правило, за основу
построения сети берут технологическую
взаимосвязь и последовательность
составляющих ее работ. Ресурсные
ограничения на этой стадии разработки
в основном не учитывают.
После
того как построен первый вариант сети,
проверяют правильность и точность
ее построения. Для этого всю сеть
просматривают от исходного события к
завершающему и обратно. У каждого
события проверяют, все ли предшествующие
работы необходимы для того, чтобы начать
следующие за ними работы. Детально
проверяют все сложные события.
Если
в процессе проверки выявляют те или
иные неточности в топологии сети, то
ошибки направляют включением
дополнительных событий и зависимостей,
с помощью которых устраняют неверные
связи и зависимости и восстанавливают
логику сетевого графика.
Первоначальный
вариант сети в большинстве случаев
необходимо графически упорядочить.
График перестраивают таким образом,
чтобы уменьшить количество взаимно
пересекающихся работ и зависимостей
и расположить работы и события
соответственно последовательности
протекаемого процесса.
Рисунок
6.6
- Пример неправильного построения
участка сети с недопустимыми тупиками
(событие 4) и хвостами (событие 6)
57

