2.4.2 Быстроходная ступень
а) Межосевое расстояние.
,
где знак «+» ( в скобках) относят к внешнему зацеплению, «–» – к внутреннему;
Т1 – вращающий момент на шестерне (наибольший из длительно действующий); Т1 = Т2 = 92,6 Н·м
U – передаточное число для быстроходной ступени.
Коэффициент К в зависимости от поверхностной твердости Н1 и Н2 зубьев шестерни и колеса соответственно выбираем К = 6.
мм
Окружную скорость υ, м/с, вычисляют по формуле
м/с
Степень точности зубчатой передачи по [1, т. 2.5 с. 17], выбираем nст = 9
Уточняем предварительно найденное межосевое расстояние
,
где Ка = 410 – для косозубых колес, МПа1/3;
[σ]Н – 1185 МПа.
Ψba – коэффициент ширины принимают в зависимости от положения колес относительно опор. При симметричном расположении Ψba = 0,315…0,5 → Ψba = 0,4
Коэффициент нагрузки в расчетах на контактную прочность
Коэффициент КНυ учитывает внутреннюю динамику нагружения. Принимаем по [1, т. 2.6 с. 17] КНυ = 1,01
Коэффициент КНβ учитывает неравномерность распределения нагрузки по длине контактных линий.
Ψbd = 1,2 → по [1, т. 2.7 стр. 19] = 1,48
,
где КНω – коэффициент, учитывающий приработку зубьев.
По [1, т. 2.8 стр. 19] КНω = 0,8
Коэффициент КНα определяют по формуле
мм
При крупносерийном производстве редукторов аω округляют до ближайшего стандартного значения: аω = 100 мм.
б) Предварительные основные размеры колеса.
Делительный
диаметр:
мм
Ширина:
мм
Ширину колеса после вычисления округляют в ближайшую сторону до стандартного числа: b2 = 40 → b2 = 40 мм.
в) Модуль передачи.
мм
,
где Кm = 2,8·103
Коэффициент нагрузки при расчете по напряжениям изгиба
Коэффициент KFυ учитывает внутреннюю динамику нагружения. Значение KFυ принимаем по [1, т. 2.9 стр. 20], выбираем KFυ = 1,01
KFβ – коэффициент, учитывающий неравномерность распределения напряжений у основания зубьев по ширине зубчатого венца
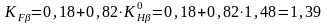
KFα – коэффициент, учитывающий влияние погрешностей изготовления шестерни и колеса на распределение нагрузки между зубьями.
мм
m = 1,5 мм
д) Суммарное число зубьев и угол наклона.
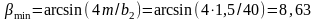
е) Число зубьев шестерни и колеса.
Число зубьев шестерни
, z1MIN = 17
→
z1
= 21
Число зубьев колеса
ж) Фактическое передаточное число.
Фактическое значение отличается от номинального не более чем на 4% (0,38%)
з) Диаметры колес.
Делительные диаметры d:
Шестерни………………………..
мм
Колеса
внешнего зацепления…..
мм
Диаметры da и df окружностей вершин и впадин зубьев колес внешнего зацепления:
,
где х1 и х2 – коэффициенты смещения у шестерни и колеса
х1 = х2 = 0;
= 0 - коэффициент воспринимаемого смещения;
мм
мм
мм
мм
и) Размеры заготовок
Dзаг=da1+6=34,82+6=40,82
Dзаг<Dпр
40,82<200
Sзаг=b2+4=40+4=44
Sзаг<Sпр
44<125
к) Проверка зубьев по контактным напряжениям.
,
где Zσ = 8400, [σ]Н =1185 МПа
МПа (не более 5%)
л) Силы в зацеплении
Окружная
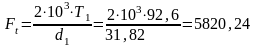H
Радиальная
Н
Осевая
Fa
=
м) Проверка зубьев колес по напряжениям изгиба.
Расчетное напряжение изгиба:
в зубьях колеса
, [σ]F2 = 619,35 МПа
в зубьях шестерни
, [σ]F1 = 619,35 МПа
Значения коэффициента YFS, учитывающего форму зуба и концентрацию напряжений, в зависимости от приведенного числа зубьев и коэффициента смещения для внешнего зацепления принимают по [1, т. 2.10, с. 24]: zυ = 111/0,97=114,43, берем YFS2 = 3,59; zυ = 21/0,97=21,65, берем YFS1 = 4,08
Значение коэффициента Yβ = 1 – β/100= 0,919
Значение коэффициента Yε = 0,65 (для косозубых передач)
МПа
МПа
н) Проверочный расчет на прочность зубьев при действии пиковой нагрузки
Кпер=2,2
