6.Логические основы устройства компьютера. Логические схемы.
Логические схемы.
Удобным способом представления логических выражении являются логические схемы. Вот как изображаются на таких схемах три основные логические операции:
Схематическое изображение логических операции
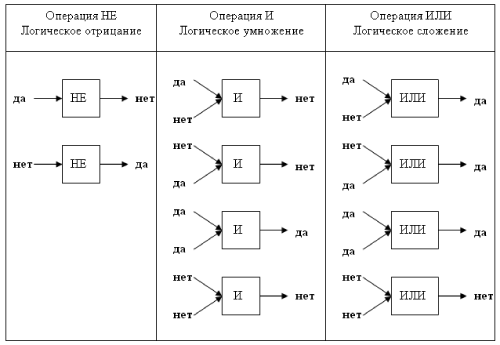
В этой использованы следующие обозначения: 1-истина; 0-ложь;
И, ИЛИ ,НЕ-логические операции(логические элементы).
Цифры в начале входящих стрелок-результаты операнды; цифры в конце выходящих стрелок- результаты операции.
Данная таблица-та же таблица истинности, только представленная в форме логических схем. В такой форме удобно изображать цепочки логических операции и производить их вычисления.
Пример 1. Для вычисления логического выражения: 1 или 0 и 1 нарисовать схему, отражающую последовательность выполнения логических операции. По схеме вычислить значение логического выражения.
Решение.
1
И
ИЛИ
0
1
Здесь наглядно отражено то, что первый выполняется операция и, затем или. Теперь в порядке слева-направо выполняется операция к выходящим стрелкам результаты операции:
1
И
ИЛИ
0
1
В результате получилась 1, т.е. истина
Пример 2. Дано выражение: не (1и(0 или 1)и 1).
Вычислить значение выражения с помощью логической схемы.
Решение. Логическая схема с результатами вычислений выглядит так:
1
И
ИЛИ
И
не
0 0
1
1
6.1. Базовые логические элементы
Базовые логические элементы реализуют рассмотренные выше нами три основные логические операции:
Логический элемент «И»- логическое умножение;
Логический элемент «ИЛИ»- логическое сложение;
Логический элемент «НЕ»- логическое отрицание.
Поскольку любая логическая операция может быть представлена в виде комбинации трех основных, любые устройства компьютера, производящие обработку или хранение информации, могут быть собраны из базовых логических элементов, как из «кирпичиков».
Логические элементы компьютера оперируют с сигналами, представляющими собой электрические импульсы. Есть импульс-логический смысл сигнала -1, нет импульса-0.
Логический элемент «И».
На выходы А и В логического элемента подаются два сигнала (00,01,10 или 11). На выходе получается сигнал 0 или 1 в соответствии с таблицей истинности операции логического умножения.
Логический элемент «И»
A
И
(0,0,1,1)
F(0,0,0,1)
B (0,0,0,1)
Логический элемент «ИЛИ»
A
ИЛИ
F(0,1,1,1)
B (0,0,0,1)
Логический элемент «НЕ»
И
A
(0,1) F(1,0)
6.2 Сумматор двоичных чисел
Полусумматор.
При сложении двоичных чисел в каждом разряде образуется сумма и при этом возможен перенос в старший разряд. Введем обозначения слагаемых(А,В) и суммы (S). Таблица сложения одноразрядных двоичных чисел с учетом переноса в старший разряд выглядит следующим образом:
Слагаемые |
Перенос |
Сумма |
|
А |
В |
Р |
С |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
Из этой таблицы видно, что перенос можно реализовать с помощью операции логического умножения:
P=A&B
Для определения суммы можно применить следующее логическое выражение:
S=(AVB)&(
Таблица
истинности логической функции
S=(AVB)&(
А |
В |
AVB |
A&B |
|
(AVB)&( |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
На основе полученных логических выражений можно построить из базовых логических элементов схему сложения одноразрядных двоичных чисел.
Полусумматор двоичных чисел
A
И
A&B
B
НЕ
И
ИЛИ
A&B
(AVB)&(
AVB
Данная схема называется полусумматором, так как реализует суммирование одноразрядных двоичных чисел без учета переноса из младшего разряда.
Полный одноразрядный сумматор.
Полный
одноразрядный сумматор имеет три входа
А,В-слагаемое и 
-перенос
из младшего разряда и два выхода: сумму
S и перенос Р. Таблица
сложения в этом случае будет иметь вид:
Слагаемые |
Перенос из младшего разряда |
Перенос |
Сумма |
|
А |
В |
Р0 |
Р |
С |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
Идея построения полного сумматора точно такая же, как и полусумматора.
Логическое выражение для вычисления суммы в полном сумматоре принимает вид:
S=(AVBV
)&
V(A&B&
)
Многоразрядный сумматор.
Многоразрядный сумматор процессора состоит из полных одноразрядных сумматоров. На каждый разряд ставится одноразрядный сумматор, причем выход (перенос) сумматора младшего разряда подключается ко входу старшего разряда.