3. Основные модели источников ошибок

3.1. Описание источника ошибок на основе цепей Маркова

Схема М. Рассмотрим представление последовательности {Е_i}.

Пусть k-ичный процесс состояний {С_i}, с_i=0,1,…,k-1 есть простая цепь Маркова. Вероятность того или иного из двух возможных значений e_i на данной (i-й) позиции определится значением состояния c_i на этой позиции, т.е. P(e₀/c₀)=P(e/c)=_ce, где _ce=1-_e для e=0 и _ce=_e для e=1. Таким образом, статистика полностью определяется матрицей переходных вероятностей Pc_-1c₀ порядка k

.

Если _с - вероятность ошибки в с-м состоянии, то вероятность ошибки в канале , где Р_с - финальная вероятность с-го состояния, определяемая по формуле , .

Обычно состояния канала могут быть разделены на две группы, в одной из которых вероятности ошибок значительно ниже, чем во второй группе. Состояния первой группы называют хорошими, а состояния второй группы – плохими состояниями. Хорошие состояния имеют номера с=0,1,…,r-1, а плохие состояния – с=r,…, k-1. Матрица переходных вероятностей примет вид

, , , , .

3.2. Описание источника ошибок на основе процессов восстановления

Схема В. Последовательность ошибок {Е_i} разбивается на отрезки (серии символов) двух видов, пакеты ошибок и промежутки между ними. В каждом из отрезков возникают независимые ошибки с вероятностями ₁ и ₀, причем ₁₀. Длины промежутков  (=1,2,…) и длины пакетов l независимы в совокупности. Поэтому статистика {Е_i} полностью определяется одномерным распределением Р() и Р(l), а также вероятностями ₁ и ₀. Таким образом, канал имеет два состояния – хорошее и плохое (k=2), последовательность состояний {C_i}={D_i} является процессом восстановления с конечным временем. Если ₁=0,5, ₀=0, то {C_i} совпадает с последовательностью элементарных состояний {S_i}. Если ₁=1, ₀=0 – с последовательностью ошибок {Е_i}. Если ₁=₀, то имеем канал с независимыми ошибками.

Вероятность попадания символа в пакет ошибок определится формулой

.

Вероятность того, что данная позиция является началом пакета ошибок и равная ей вероятность того, что данный символ является началом промежутка между пакетами, равна

,

поэтому вероятность ошибки определится формулой

.

Вероятность P_n(t) того, что блок символов длины n содержит t ошибок, при условии независимости ошибок в пакете и в промежутке между ними, определится формулой

.

Если ошибки возможны только в пакетах (₀=0, ₁=), то

.

3.3. Описание источника ошибок на основе процессов накопления

Схема Н. В данной схеме модель источника ошибок отличается от ранее рассмотренных схем допустимостью перекрытия пакетов. Любая позиция последовательности {Е_i} может стать началом пакета ошибок, причем длины интервалов между началами пакетов _Н (_Н=0,1,…) являются случайными независимыми величинами. Поэтому процесс {D_i}, где D_i=1 для позиций, являющихся началами пакетов, и D_i=0 для позиций, не являющихся началами пакетов, представляет собой процесс с мгновенным восстановлением. Статистика этого процесса полностью определяется распределением вероятностей Р(_Н) длин между пакетами.

Длины пакетов l_Н (l_Н=1,2,…) являются значениями независимых случайных величин и определяются распределениями Р(l_Н). В пределах каждого отдельного пакета (не перекрывающегося с другими пакетами) ошибки независимы и имеют вероятность возникновения ошибки . Таким образом, статистика {Е_i} по схеме Н полностью определяется двумя одномерными распределениями вероятностей – длин пакетов Р(l_Н) и интервалов между началами пакетов Р(_Н), т.е. статистикой последовательности пар независимых чисел {_Н, l_Н} и вероятностью ошибки в пакете .

На рис..1.7 приведен пример построения последовательности {2,3},{3,4},{1,5},{6,8},{0,2} для схемы Н.

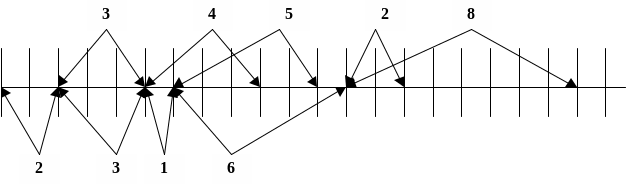
Рис.1.7

Для данной модели, в отличие от схемы В, независимы не промежутки между пакетами, а интервалы между пакетами. Это обуславливает возможность перекрытия и примыкания пакетов (возможно перекрытие нескольких пакетов).

Последовательность ошибок {Е_i} для данной модели может быть представлена последовательностью состояний {С_i}, в пределах которых ошибки независимы и имеют одинаковые вероятности. Число состояний – более двух и может быть сколь угодно большим, т.к. на участке наложения пакетов вероятность ошибки может превышать вероятность ошибки  в каждом отдельном пакете. Действительно, в пределах каждого пакета позиции поражаются с вероятностью 2 (см. рис. 1.7), следовательно, вероятность поражения позиции на участке наложения n пакетов равна (1-(1-2)ⁿ), а вероятность ошибки равна 0,5[1-(1-2)ⁿ]. С ростом числа наложений пакетов вероятность поражения стремится к единице, а вероятность ошибки - к 0,5. При =0,5 последовательность {Е_i} может быть представлена двоичной последовательностью элементарных состояний {C_i}={S_i}, не являющейся процессом восстановления.

Перекрытие пакетов усложняет подсчеты. Просто определить вероятность того, что данная случайная величина является началом пакета:

.

Сложность определяется тем, что сумма длин пакетов на некотором участке не дает возможность непосредственно найти распределение вероятностей числа пораженных символов и ошибок.

Если взять пакеты длиной в один символ, т.е. Р(l_Н=1)=1 и Р(l_Н>1)=0, то процесс состояний {C_i} вырождается в процессе с мгновенным восстановлением (перекрытие пакетов невозможно). Если распределение Р(l_Н) геометрично, то канал не будет обладать памятью, а вероятность ошибки определится формулой

.