14. Графическое изображение рядов распределения (полигон, гистограмма, кумулята).

Статистические ряды распределения представляют собой упорядоченное расположение единиц изучаемой совокупности на группы по группировочному признаку.

Различают атрибутивные и вариационные ряды распределения.

Атрибутивный – это ряд распределения, построенный по качественным признакам. Он характеризует состав совокупности по различным существенным признакам. По количественному признаку строится вариационный ряд распределения. Он состоит из частоты (численности) отдельных вариантов или каждой группы вариационного ряда. Данные числа показывают, насколько часто встречаются различные варианты (значения признака) в ряду распределения.

Особым видом графиков являются диаграммы распределения величин, представленных вариационным рядом. Это гистограмма, полигон, кумулята.

Гистограмма - это представление данных в столбиковой форме. Каждый столбик представляет величину отдельного уровня исследуемого статистического ряда. Гистограмма используется для изображения только интервальных рядов. У всех столбиков, составляющих диаграмму, переменной величиной является только одно измерение.

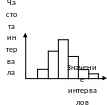
Рис. 1 Гистограмма

П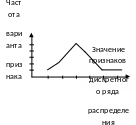 олигон - это вид диаграммы в которой при помощи отрезков соединяются точки середин координат сторон прямоугольника. Полигон обязательно пересекает ось Х по краям в точках принятых в масштабе на величину интервалов от середины крайних прямоугольников, половины крайних координат. Если с лева отрезок должен уйти за край оси Y, то есть приобрести отрицательный характер, то начало левого отрезка будет совпадать с началом координат на диаграмме. Полигон применяется для изображения как дискретных, так и интервальных рядов.

Рис. 2 Полигон распределения

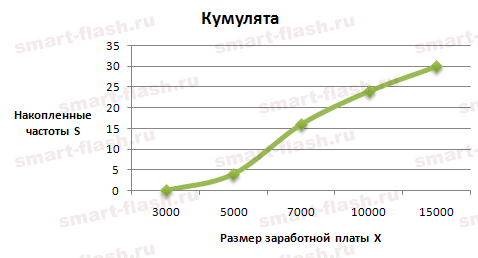
Кумулята - ломаная кривая, строящаяся на основе прямоугольной системы координат, когда по оси Х откладываются значения признака, а по оси У – накопленные частоты. Для дискретных рядов на оси откладываются сами значения признака, а для интервальных – середины интервалов. это линейное построения диаграммы по накопленным частотам, которые определяются последовательным суммированием частот. Накопление частоты показывают сколько единиц совокупности имеют значения признака не больше чем рассматриваемое значение.

При построении кумуляты накопленная частота (частость) соответствующего интервала присваивается его верхней границе:

15. Средняя величина статистики, ее сущность и условия применения

В качестве одной из важнейших характеристик вариационного ряда является средняя величина, представляющая обобщенную коли­чественную характеристику признака в статистической совокупности однотипных явлений по одному из варьирующих признаков в кон­кретных условиях места и времени. Важнейшим свойством средней является то, что она отражает то общее, что присуще всем единицам исследуемой совокупности. Сущность средней и заключается в том, что в ней взаимопогашаются отклонения значений признака отдельных единиц совокупности, обусловленные действием случайных факторов, и учитываются изменения, вызванные действием основных факторов. Это позволяет средней отражать типичный уровень признака и абстра­гироваться от индивидуальных особенностей, присущих отдельным единицам. Типичность средней связана с однородностью статистиче­ской совокупности. Если совокупность неоднородна, то метод средних должен использоваться в сочетании с методом группировок, т.е. общие средние должны быть заменены или дополнены групповыми средними.

Средние величины - это обобщающие показатели, в которых на­ходят выражение действие общих условий, закономерность изучаемо­го явления. Средняя должна ориентироваться на определенную величину, связанную со всеми единицами этой совокупности. Ее можно пред­ставить в виде функции:

f(x1,x₂,...,x_n) = f(x,x,...,x).

Для характеристики неоднородной совокупности ее необходимо расчленить на группы и находить среднюю по каждой из них. В отли­чие от средней, абсолютная величина, характеризующая уровень при­знака отдельной единицы совокупности, не позволяет сравнивать зна­чения признака из единиц, относящихся к разным совокупностям.

К некоторым общим принципам применения средних величин относятся следующие:

1. при определении средних величин нужно исходить из качест­венного содержания усредняемого признака, учитывать взаимосвязь изучаемых признаков, все имеющиеся для расчета данные;

2. рассчитывается, прежде всего, по однородной совокупности;

3. общие средние подкрепляются групповыми средними;

4) необходим обоснованный выбор единицы совокупности.