25. Понятие выборочного наблюдения.

Под выборочным наблюдением (сокращенно выборка) понимается не сплошное наблюдение, при котором статистическому обследованию (наблюдению) подвергается не всё, а отдельные единицы, отобранные с соблюдением определенных условий.

26. Генеральная и выборочная совокупности

Данные термины используются в выборочном наблюдении.

Выборочное наблюдение – вид несплошного наблюдения, при котором из общей (генеральной совокупности) отбирается посредством метода случайного отбора некоторая часть, называемая выборочной совокупностью; обобщающие показатели, характеризующие эту часть совокупности, распространяются на всю совокупность.

Применение выборочного метода связано с возникновением ошибок репрезентативности, которые представляют собой разность между обобщающими показателями генеральной выборочной совокупностей.

Выборочная совокупность может формироваться разными методами. Может иметь место индивидуальный отбор (когда отбирается каждый раз одна единица совокупности) или серийный (отбор производится сериями, гнездами, упаковками и т.п., и в них обследуются все единицы).

После обследования отобранные единицы могут быть возвращены в генеральную совокупность, где имеют одинаковую со всеми единицами вероятность вновь попасть в выборку – повторный отбор либо могут не участвовать в дальнейшем отборе – бесповторный отбор.

27. Средняя и предельная ошибки выборки.

Выборочное наблюдение относится к разновидности несплошного наблюдения. Оно охватывает отобранную часть единиц генеральной совокупности. Цель выборочного наблюдения - по отобранной части единиц дать характеристику всей совокупности единиц. Чтобы отобранная часть была репрезентативна (т.е. представляла всю совокупность единиц), выборочное наблюдение должно быть специально организовано. Следовательно, в отличие от генеральной совокупности, представляющей всю совокупность исследуемых единиц, выборочная совокупность представляет ту часть единиц генеральной совокупности, которая является объектом непосредственного наблюдения.

Следует сразу же иметь в виду, что при сопоставлении показателей по результатам выборочного исследования с характеристиками для всей генеральной совокупности могут иметь место отклонения. Величина этих отклонений называется ошибкой наблюдения, которая может быть или ошибкой регистрации (несовершенство технических условий), или ошибкой репрезентативности (случайное или систематическое нарушение правил при отборе единиц).

п - объем выборочной совокупности;

S² - выборочная дисперсия;

Расчет средней ошибки случайной выборки производится следующим образом:

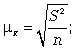
Расчет предельной ошибки    случайной выборки:

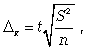
При этом t как коэффициент кратности средней ошибки выборки зависит от вероятности, с которой гарантируется величина предельной ошибки выборки.

Среднее квадратическое отклонение S и среднее квадратическое отклонение в квадрате S², которое называют дисперсией. Дисперсия есть не что иное, как средний квадрат отклонений индивидуальных значений признака от его средней величины.