Неравномерность товара (материала) по различным признакам

Равномерность материалов и изделий по их строению и свойствам является важной товароведной характеристикой, так как от нее зависят практически все этапы производственного цикла, а также потребительские свойства.

Неравномерность может проявляться в видимой и скрытой формах. Это разграничение условно, оно обусловливается в основном применяемыми методами оценки неравномерности.

Неравномерность "видимая" устанавливается непосредственным наблюдением или путем сравнения объекта с нормальным образцом (эталоном). Так определяется, например, равномерность окраски материала, однородность лаковых покрытий, чистота поверхности металла, дерева, дефекты нити (утолщения, узлы) и т. д. Аналогичный принцип наиболее часто используют при оценке неравномерности свойств товара.

Если неравномерность проявляется в завуалированной форме (причем ее влияние на качество материала может быть даже большим), то ее определение основывается на результатах лабораторных испытаний.

При повторных определениях какого-либо признака наблюдается, что результаты определения не совпадают, отклоняясь один от другого в большей или меньшей мере.

Наблюдаемые колебания могут быть вызваны неточностью определения, неравномерностью материала или тем и другим одновременно.

Точность показаний приборов и результатов механических или иных определений должна быть известной, и, таким} образом, колебания результатов, превосходящие точность лабораторных определений, должны быть отнесены за счет неравномерности испытуемого материала. Если колебания в результатах не превосходят точности лабораторных определений, то судить по этим колебаниям о неравномерности материала не представляется возможным. При данной точности лабораторных определений, когда колебания в отдель

ных результатах переходят границы точности определений, можно оценить неравномерность материала по изучаемому признаку.

При проведении товароведных испытаний возникают следующие вопросы, связанные с оценкой неравномерности: какова величина неравномерности, если судить о ней по полученным результатам испытаний; какова точность среднего результата, полученного из п испытаний при неравномерности Н; какое количество повторных испытаний п. должно быть проведено при неравномерности материала Н для получения результата с заданной точностью. Оценка неравномерности производится различными методами, которые ниже кратко описаны.

Способы вычисления неровноты

В товароведных исследованиях равномерность материала принято во многих случаях характеризовать показателем его неровноты. Для оценки нербвноты по данному признаку (тонине, прочности и т. д.) необходимо путем лабораторных испытаний получить ряд значений этого признака и вычислить среднеарифметическое его значение — М_ср. По величине М_ср все значения ряда делят на две группы: меньшие М_ср и большие М_ср. Далее вычисляют среднеарифметическое значение из меньших М_м и среднеарифметическое значение из больших — М₆.

Имея три величины М_ср, М_м и М₆, неровноту по данному признаку в процентах вычисляют по одной из следующих формул:

Из приведенных формул видно, что при всех расчетах неровнотой называется отклонение от среднеарифметического значения, отнесенное к средней арифметической, выраженное в процентах.

В зависимости от того, интересует ли нас при исследовании признака полный диапазон колебаний, отклонения в сторону больших или меньших значений, применяют ту или другую формулу.

В большинстве случаев наибольшее практическое значение имеет величина отклонений в сторону меньших значений, при этом важно и количество меньших значений в общем числе значений п. Последнее обстоятельство учитывается в следующей формуле неровноты, получившей наибольшее применение:

где: а — абсолютная величина отклонения очередного значения признака от М_ср, п — число всех испытаний; при числе испытаний п < 50 величина п уменьшается на 1.

С достаточным приближением коэффициент вариации может быть подсчитан, если известна неровнота, расчет ведется по формуле:

С = А-Н

где: С — коэффициент вариации в процентах;

Н — неровнота по формуле (см. выше);

А — коэффициент, зависящий от числа испытаний.

Штапельная диаграмма. Наглядный метод оценки неравномерности состоит в построении так называемой штапельной диаграммы (рис. 5.1). При ее построении количественные характеристики исследуемого признака располагаются в убывающем порядке и откладываются в диаграмме, в которой по вертикали откладывается величина признака, а по горизонтали порядковый номер результата. Штапельная диаграмма применяется, в частности, для характеристики длины волокон в пучке волокон, называемом штапелем, откуда она и получила свое название.

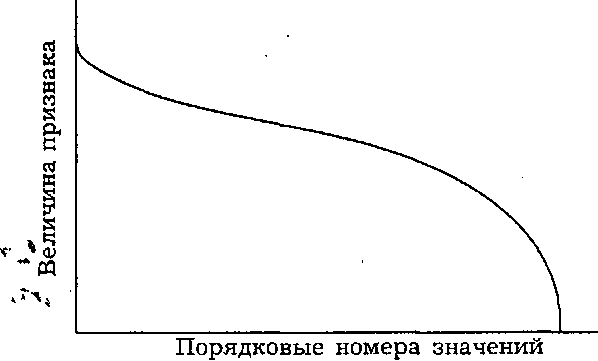
Рис. 5.1. Штапельная диаграмма

Кривая распределения. На рис. 5.2 представлена кривая распределения показателей прочности, полученных при проведении 200 обрывов швейных ниток.

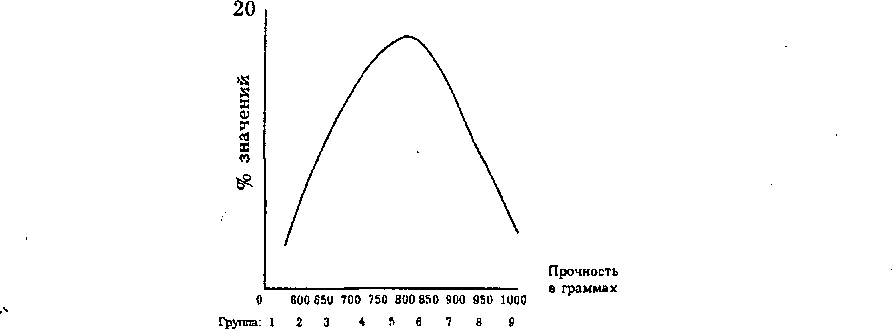
К ак видно из диаграммы, по горизонтали откладываются значения признака, а по вертикали — количество значений признака в процентах. Проведя через полученные точки плавную кривую, мы получим кривую распределения. Из диаграммы видно, что вершина кривой характеризует те значения признака, которые наблюдались в наибольшем количестве (обладали наибольшей частотой); значение признака, соответствующее вершине кривой, называется модальной средней, или модой распределения.

Эта вершина соответствует среднему значению прочности для группы значений № 5, причем в данном случае средняя модальная почти совпадает со средней арифметической.