3.4 Определение уравновешивающей силы методом рычага жуковского

3.4.1 Раскладываем моменты пар сил инерции, действующие на звенья, на пары сил:

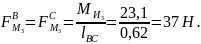
3.4.2 Взяв план скоростей из кинематического анализа механизма (чертеж…), чертим его, повернув на 90°.

3.4.3 Используя теорему о подобии для планов скоростей, в соответствующие точки на планах прикладываем приложенные к ним силы. Получили рычаг Жуковского.

3.4.4 Составляем уравнение моментов относительно полюса и находим из него уравновешивающую силу. Плечи сил измеряем на чертеже в миллиметрах.

3.4.5 Вычисляем относительную погрешность определения разными способами

где – величины уравновешивающей силы, определённые методами рычага Жуковского и планов сил соответственно.

Расхождение не превышает 5%. Следовательно, можно считать, что силовой расчёт выполнен правильно обоими методами.

4 Синтез зубчатого зацепления

4.1 Исходные данные

4.1.1 Число зубьев колес z₁ = 13 и z₂ = 25.

4.1.2 Модуль зацепления m = 8 мм .

4.1.3 Критерии качества

– Коэффициент торцевого перекрытия ε 

– Коэффициент удельного скольжения зубьев колеса и шестерни должны быть равны

– Подрез зубьев шестерни и колеса не разрешается

4.2 Определение коэффициентов смещения

4.2.1 Исходя из заданных чисел зубьев z₁ = 13 и z₂ = 25 по ближайшему бло­кирующему контуру для z₁ = 13 и z₂ = 25 выбираем коэффициенты смещения таким образом, чтобы обеспечить равенство удельных скольжений λ₁ = λ₂, величину коэф­фициента перекрытия ε ≥ 1,2 и толщину зуба шестерни на окружности вершин S_a ≥ 0,25 m. Принимаем предварительно x₁´= 0,5 ; x₂´= 0,2 .

4.2.2 Инволюта угла зацепления:

Угол зацепления α _w ≈ 24º 33´.

4.2.3 Предварительное межосевое расстояние:

4.2.4 Округляем межосевое расстояние до ближайшего значение из ряда нормальных линейных размеров 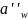= 160 мм .

4.2.5 Уточняем угол зацепления:

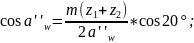
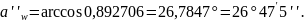
4.2.6 Сумма коэффициентов смещения:

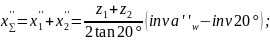
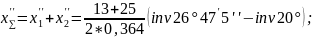
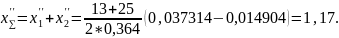
4.2.7 По блокирующему контору с учетом п.4.3 распределяем 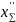по колесам. Принимаем 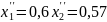. Эта точка лежит на прямой λ₁ = λ₂ выше кривой ε 

4.2.8 Исследуем возможность увеличения ε путем уменьшения x_Σ. C этой целью принимаем межосевое расстояние из ряда нормальных линейных размеров ближайшее меньшее вычисленному в п.5.3 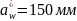и повторяем расчеты по п.п. 5.5 и 5.6.

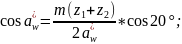
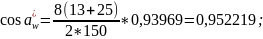
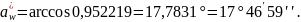
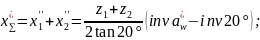
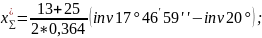
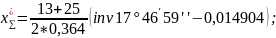
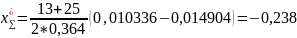
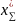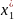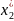4.2.9 Пытаемся распределить по колесам. Устанавливаем, что при любых значениях и точка с такими координатами лежит вне блокирующего контура что не допустимо.

4.2.10 Принимаем промежуточное значение межосевого расстояния a_w = 155 и вновь повторяем вычисления.

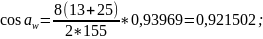
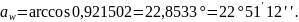
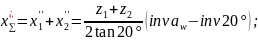
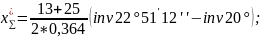
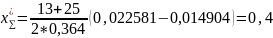
4.2.11 С учетом п. 1.4 по блокирующему контуру окончательно принимаем

x₁´= 0,45 ; x₂´= – 0,05. При этом видим, что толщина зуба шестерни по окружности вершин больше минимально допустимого значения S_a1 = 0,25m, а других ограничений не задано.

4.3 Рачсеты размеров

4.3.1 Радиусы начальных окружностей:

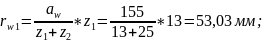
Проверка:

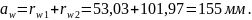
4.3.2 Радиусы делительных окружностей:

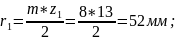
4.3.3 Радиусы основных окружностей:

4.3.4 Радиусы окружностей впадин:

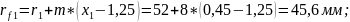
4.3.5 Радиусы окружностей вершин:

4.3.6 Шаг по делительной окружности:

4.3.7 Угловые шаги:

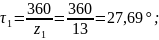
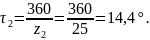
4.3.8 Вычисляем размеры зубьев :

- высоты головок

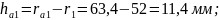
- высоты ножек

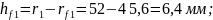
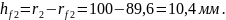
- высоты зубьев

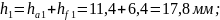
Проверка

h₁ = h₂

- толщины зубьев по делительным окружностям

4.3.9 Проверяем правильность расчетов радиальных размеров через высоту зубьев:

-коэффициент воспринимаемого смещения

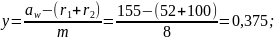
-коэффициент уравнительного смещения

-высоты зубьев

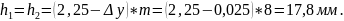
Результат совпал с п. 6.8. Расчеты выполнены верно.

4.3.10 Толщина зубьев шестерни по окружности вершин:

где

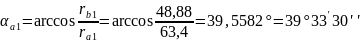
4.3.11 Проверяем отсутствие заострения зубьев шестерни:

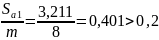
4.3.12 Длина теоретической линии зацепления:

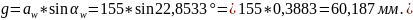
4.3.13 Размеры общих нормалей.

где

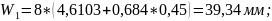
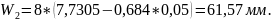
4.3.14 Вычисленные размеры сводим в таблицу

Таблица П.1.1

Параметры зацепления
	Обозн.	Ед. изм.	Колеса
			1	2
Модуль	m	мм	8
Число зубьев	z	–	13	25
Коэффициент смещения	x	–	0,45	- 0,05
Окружной шаг по длительной окружности	p	мм	25,12
Угловой шаг	τ	…°	27,69	14,4
Межосевое расстояние	aw	мм	155
Угол зацепления	αw	…°
Длина теоретической линии зацепления	g	мм	60,187
Радиус делительной окружности	r	мм	52	100
Радиус основной окружности	rb	мм	48,88	94
Радиус начальной окружности	rw	мм	53,03	101,97
Радиус окружности вершин	ra	мм	63,4	107,4
Радиус окружности впадин	rf	мм	45,6	89,6
Высота головки зуба	ha	мм	11,4	7,4
Высота ножки зуба	hf	мм	6,4	10,4
Высота зуба	h	мм	17,8	17,8
Толщина зуба по делительной окружности	S	мм	15,1808	12,2688
Длина общей нормали	W	мм	39,34	61,57
Угол перекрытия*	φα	…°
Коэффициент перекрытия	ε	–	1,41