1.4 Побудова планів прискорень

Визначимо прискорення точки А. Через те, що кривошип обертається рівномірно, точка А має тільки нормальне прискорення, яке напрямлене вздовж ланки АО до центра обертання. Значення цього прискорення

м/с².

Таблиця 1.2 Визначення швидкостей різних ланок і точок механізму

Позначення	Положення механізму
	0	2
pb, мм	0	67
, м/c	0	0,67
, мм	63	6
. м/с	0,63	006
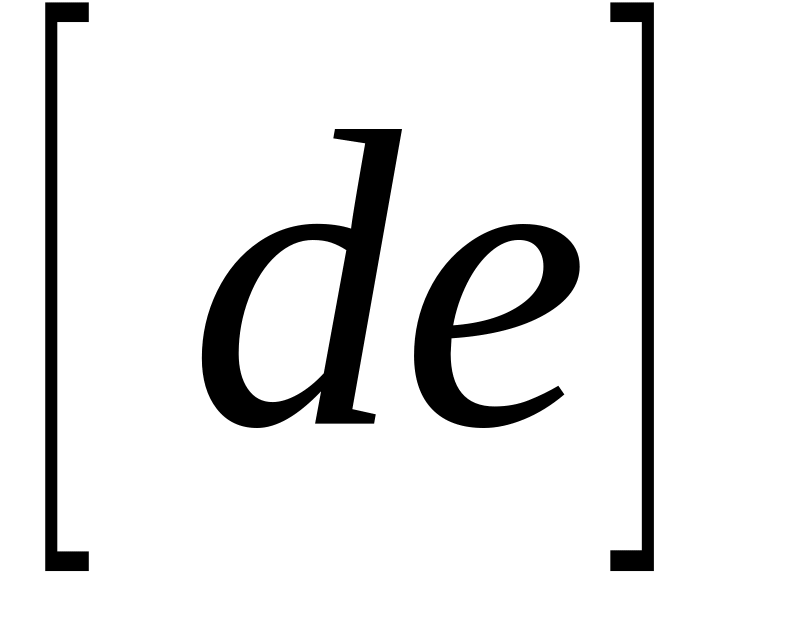, мм	0	39
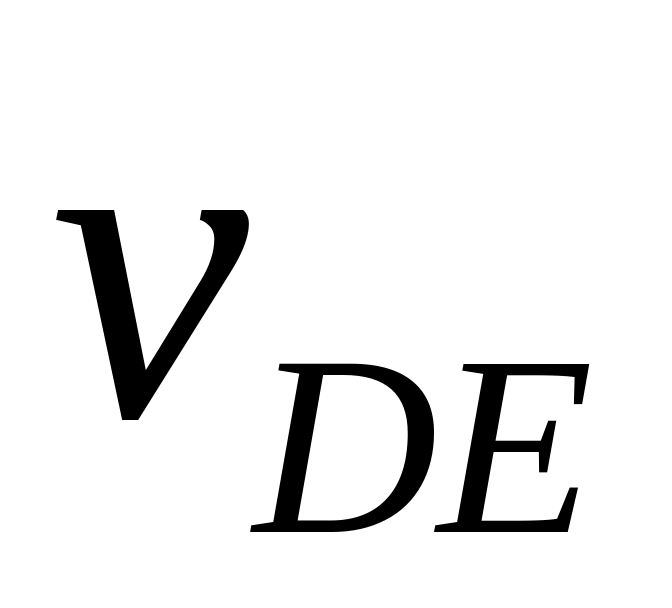, м/с	0	0,39
, мм	0	112
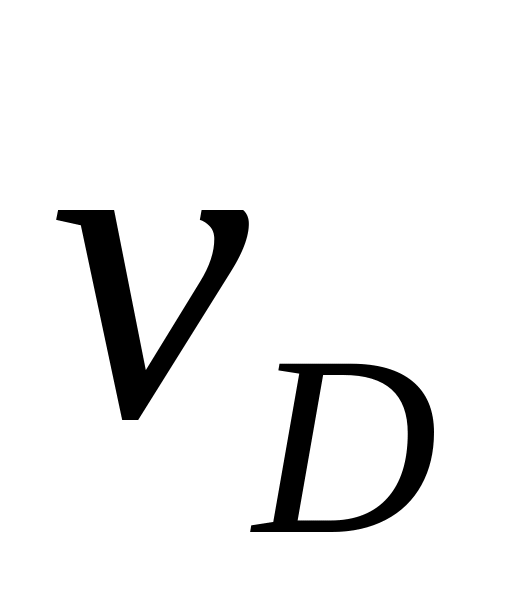, м/с	0	1,12
pе, мм	0	102
, м/c	0	1,02
, мм	31,5	66
, м/c	0,32	0,66
, мм	0	106
, м/c	0	1,06
, с-1	0,7	0,1
, с-1	0	2,2
, с-1	0	0,8

Приймемо довжину відрізка , який зображає вектор прискорення точки А таким, що дорівнює 78,8 мм.

Тоді масштаб плану прискорень

м/(с²мм).

З довільної точки , яка прийнята за полюс плану прискорень, відкладаємо паралельно ланці ОА відрізок .

Прискорення точки С дорівнює нулю, отже, точка с збігається з полюсом плану прискорень.

Прискорення точки В знаходимо, використовуючи наступні векторні рівняння:

де - вектор нормального прискорення точки В при обертанні ланки 2 відносно точки А, має напрям уздовж ланки до умовного центру обертання; - вектор дотичного прискорення точки В при обертанні ланки 2 відносно точки А; - вектор нормального прискорення точки В при обертанні ланки 3 відносно точки С, має напрям уздовж ланки до центру обертання С; - вектор дотичного прискорення точки В при обертанні ланки 3 відносно точки С.

Визначаємо значення нормальних прискорень:

м/(с²мм),

м/(с²мм).

Тоді відрізки, що зображають їх на плані прискорень:

мм (цим відрізком нехтуємо),

мм.

Будуємо план прискорень і знаходимо прискорення точки В , а також невідомі складові і :

м/(с²мм),

м/(с²мм),

м/(с²мм).

Прискорення точки D, яка належить коромислу 3, визначаємо за теоремою подібності планів прискорень, склавши пропорцію:

,

звідки мм.

Відкладаємо відрізок на продовженні відрізка .

Визначаємо прискорення точки D:

м/с².

Аналогічно визначаємо прискорення точки Е з рівнянь:

де - вектор нормального прискорення точки Е при обертанні ланки 4 відносно точки D, має напрям уздовж ланки до умовного центра обертання D; - вектор дотичного прискорення точки Е при обертанні ланки 4 відносно точки D; = 0; - вектор відносного прискорення точки відносно точки , що направлений вздовж вертикальної направляючої.

Величину нормального прискорення за формулою:

м/с².

Тоді відрізок, що зображає його на плані прискорень дорівнює:

мм (цим відрізком нехтуємо).

Будуємо план прискорень і визначаємо прискорення:

м/с²,

м/с².

Знаючи положення центрів мас S₁, S₂, S₄, за аналогією з планом швидкостей, знаходимо за правилом подібності положення точок s₁, s₂, s₄ на плані прискорень, з’єднуємо ці точки з полюсом плану прискорень, і визначаємо прискорення центрів мас:

м/с²,

м/с²,

м/с².

Значення кутових прискорень ланок 2 і 3:

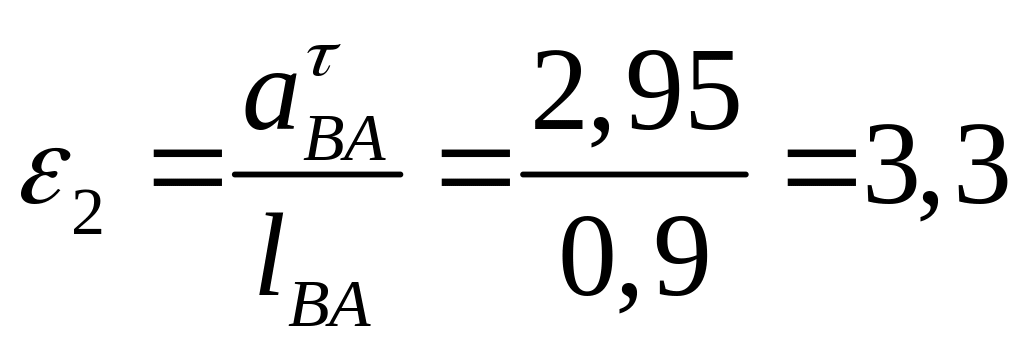с^-2,

с^-2, с^-2.

Для визначення напряму вектора переносимо вектор в точку В. Розглядаємо рух ланки 2 відносно точки А. У нашому випадку напрямок проти годинникової стрілки. Аналогічно визначаємо, що і направлені, відповідно, проти і за годинниковою стрілкою

План прискорення в нульовому положенні механізму будується аналогічно. Отримані значення відрізків, які зображають вектори прискорень, і їх значення наведено у табл. 1.3.