5. Проектный расчет валов

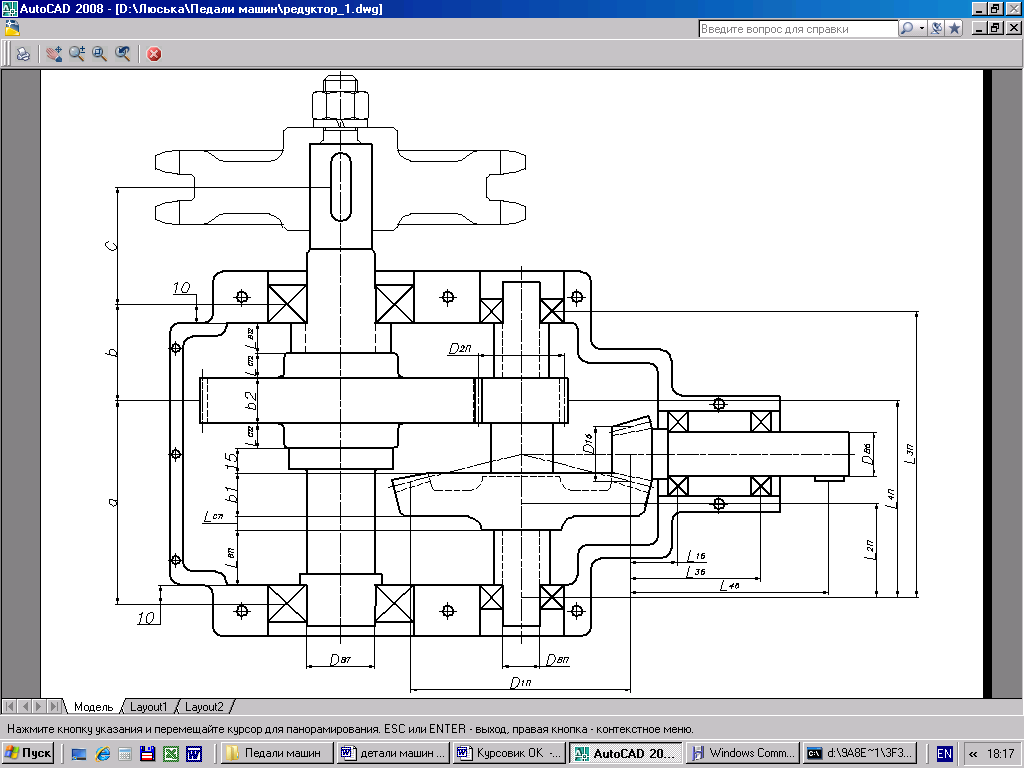
Рисунок 4.1 Расчетная схема редуктора.

1. Расчет среднего диаметра вала

Средний диаметр вала определим по формуле:

1. Расчет быстроходного вала

• вращающий момент на валу Т_б = 29,4 Нм;

• частота вращения вала n_б = 955 об/мин;

• материал вала (т.о улучшение) Сталь 40ХН,

_В = 850 МПа; _Т = 600 МПа.

20,1 мм.

По ГОСТ 6636-69 для ряда Ra20 принимаем d_б = 20 мм.

2. Расчет промежуточного вала

• вращающий момент на валу Т_П = 112,9 Нм;

• частота вращения вала n_П = 238,8 об/мин;

• материал вала (т.о цементация и закалка) Сталь 20Х,

_В = 650 МПа; _Т = 400 МПа.

28,5 мм.

По ГОСТ 6636-69 для ряда Ra20 принимаем d_П = 28 мм.

3. Расчет тихоходного вала

• вращающий момент на валу Т_Т = 338,2 Нм;

• частота вращения вала n_Т = 75,8 об/мин;

• материал вала (т.о. нормализация) Сталь 45,

_В = 600 МПа; _Т = 340 МПа.

36,5 мм.

По ГОСТ 6636-69 для ряда Ra20 принимаем d_T = 36 мм.

2. Выбор подшипника

Выбор подшипника производим по среднему диаметру вала из серии роликовые конические однорядные подшипники повышенной грузоподъемности ГОСТ 27365–87. Для диаметра d_T = 36 мм принимаем подшипник 2007108А, серия диаметров 1, серия ширин 2. с размерами: D = 68 мм; d = 40 мм; B = 19 мм; r_1Smin = 1,0 мм; r_2Smin = 1,0 мм.

3. Длинновые размеры вала

Определение размеров производим по формулам из таблицы 13.

a = 10 + L_вт1 + L_ст1 + b₁ + 15 + L_ст2 + b_W2/2;

a = 10 + 32 + 8 + 25 + 15 + 16,5 + 13,5 = 120 мм.

b = b_W2/2 + L_ст2 + L_вт2 + 10;

b = 13,5 + 16,5 + 15 + 10 = 55 мм.

;

70 мм.

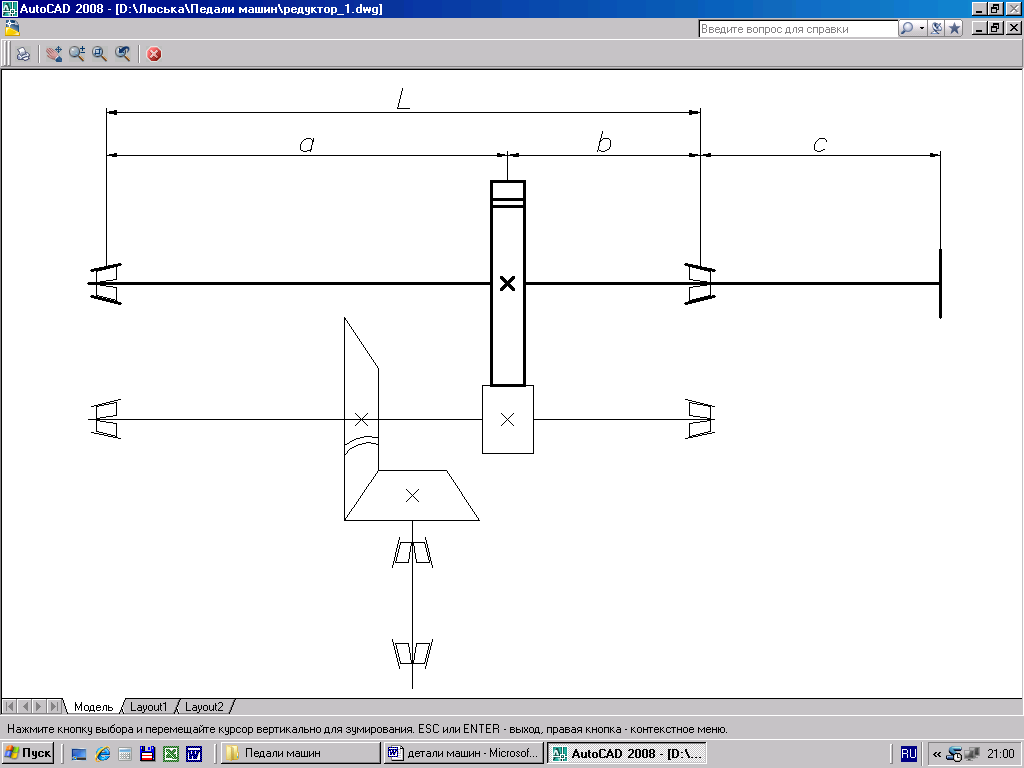
Рисунок 4.2 Расчетная схема вала.

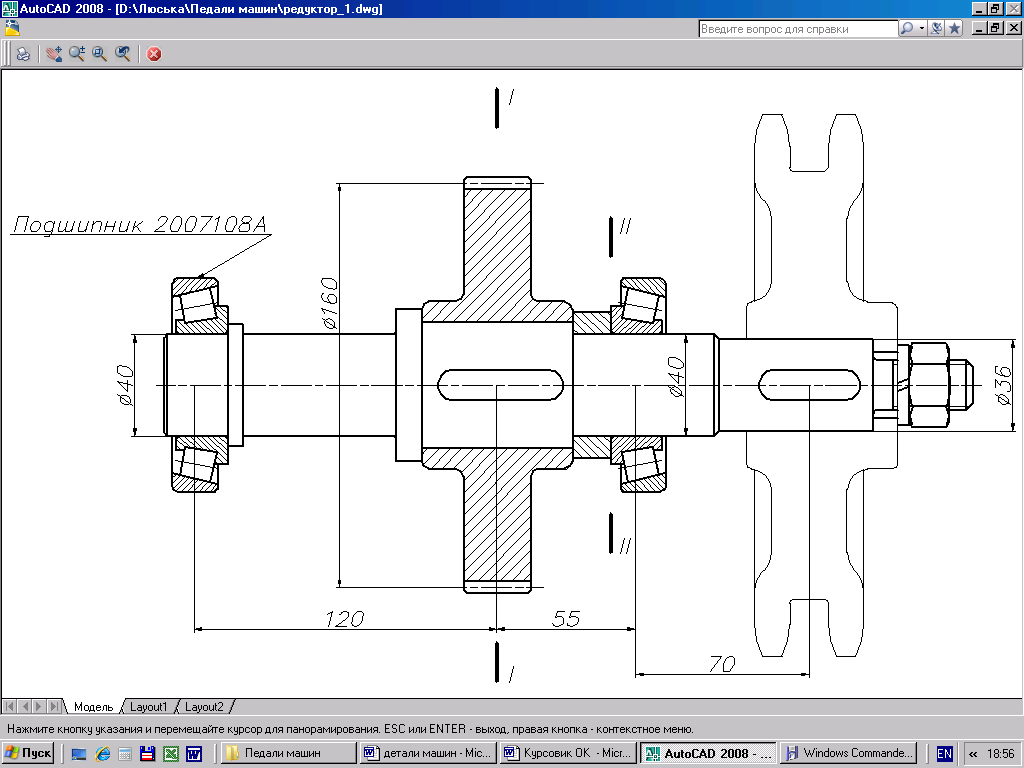
Рисунок 4.2 Эскиз выходного вала редуктора.

4. Расчет сил, приложенных к валу

   1. Силы в зацеплении

Окружное усилие F_t = 2T₁/d_2Т = 2  112,9/0,160  4516 Н.

Осевая сила F_a = F_t  tg = 0 Н, так как  = 0

Радиальная сила F_r = F_t  tg_W/cos  4516  tg20/cos0  1644 Н.

2. Нагрузка на консоли вала

Из расчета на ЭВМ передач роликовой цепью по ГОСТ 13568-75, для двухрядной цепи получено: F_M = 3838 Н.

По результатам выполненных расчетов составляем расчетную схему вала.

Р исунок 4.3 Расчетная схема вала в виде на двух опорах.

5. Построение эпюр

Вначале производим схематизацию конструкции вала. Получаем балку на двух опорах, как показано на рисунке 4.3.

Силы, действующие на вал, приложены в двух плоскостях. Согласно схеме на рисунке 4.3, радиальная сила действует в горизонтальной плоскости, а окружная и сила на консоль вала – в вертикальной плоскости. В нашем случае рационально построить эпюры для каждой плоскости отдельно, а затем, их геометрически сложить. Индексами 1 будем отмечать реакции опор вала от сил, действующих в вертикальной плоскости, а индексами 2 – реакции опор вала от сил, действующих в горизонтальной плоскости.

Вертикальная плоскость. Находим реакции опор А₁ и В₁ по схеме нагружения, как показано на рисунке 4.4.

Реакции опор определяются из системы двух уравнений для изгибающих моментов:

(М_и)_А = 0; В₁  (a + b) – F_r  a = 0

(М_и)_В = 0; –A₁  (a + b) + F_r  b = 0

М_а – изгибающий момент от осевой силы:

= 0 Нм, так как F_a = 0 Н.

Отсюда находим

В₁ = F_r  a/(a + b) = 1644  120/(120 + 55)  1127 Н;

A₁ = F_r  b/(a + b) = 1644  55/(120 + 55)  517 Н.

Для проверки правильности найденных значений воспользуемся уравнением

–F_r + A₁ + В₁ = 0; –1644+ 517 + 1127 = 0;

Изгибающий момент в сечении (под ступицей колеса) составит:

A₁  a = 517  0,12 = 62 Нм;

В₁  b = 1127  0,055 = 62 Нм.

Горизонтальная плоскость. Находим реакции опор А₂ и В₂ по схеме нагружения, как показано на рисунке 4.4.

Реакции опор определяются из системы двух уравнений для изгибающих моментов:

(М_и)_А = 0; F_t  a +В₂  (a + b) – F_M  (a + b + с) = 0

(М_и)_В = 0; –A₂  (a + b) – F_t  b – F_M  с = 0

Отсюда находим

В₂ = [F_M  (a + b + с) – F_t  a] / (a + b) = [3838  245 – 4516  120] / 175  2276,5 Н;

A₂ = – (F_t  b + F_M  с) /(a + b) = – (4516  55 + 3838  70) /(120 + 55)  –2954,5 Н.

Для проверки правильности найденных значений воспользуемся уравнением:

F_t + A₂ + В₂ – F_M = 0; 4516 – 2954,5 + 2276,5 – 3838 = 0;

A₂  a = –2276  0,12 = –354,5 Нм;

F_M  с = 3838  0,07 = 268,7 Нм.

Суммарная эпюра изгибающих моментов М_и. Эпюра получается последовательным геометрическим суммированием ординат эпюр М_и1 и М_и2. На суммарной эпюре отмечаем опасные сечения I–I и II–II, как сечения, в которых действуют наибольшие по величине изгибающие моменты, а именно:

(М_и) = = 359,9 Нм;

(М_и) = = 268,7 Нм.

Суммарные реакции опор (A_) и (B_) получаются геометрическим суммированием их проекций на вертикальную (A₁ и B₁) и горизонтальную (A₂ и B₂) плоскости:

(A_) =  3000 Н;

(B_) =  2540 Н.

Рисунок 4.4 Эпюры изгибающих и крутящего моментов вала.