Содержание

Введение 4

1 Кинематический расчет привода 6

2 Расчет цилиндрической зубчатой передачи 9

3 Расчет конической зубчатой передачи 17

4 Расчет цепной передачи на ЭВМ 27

5 Проектный расчет валов 29

6 Определение запасов сопртивления усталости 35

7 Проверка статистической прочности вала 38

8 Выбор подшипников 46

9 Выбор шпонок 50

10 Выбор муфты для быстроходного вала 54

11 Выбор корпусных деталей 54

12 Выбор смазки 55

13 Вывод 55

Список использованных источников 56

Введение

Машиностроению принадлежит ведущая роль среди других отраслей экономики, так как основные производственные процессы выполняют машины. Поэтому и технический уровень многих отраслей в значительной мере определяет уровень развития машиностроения.

«Детали машин» являются первым из расчетно–конструкторских курсов, в котором изучают основы проектирования машин и механизмов.

Любая машина (механизм) состоит из деталей.

Деталь – такая часть машины, которую изготовляют без сборочных операций. Детали бывают простыми (гайка, шпонка и т.п.) или сложными (коленчатый вал, корпус редуктора, станина станка и т.п.) Детали (частично или полностью) объединяют в узлы.

Узел представляет собой сборочную единицу, состоящую из ряда деталей, имеющих общее функциональное назначение (подшипник качения, муфта, редуктор и т.п.).

Среди большого разнообразия деталей и узлов машин выделяют такие, которые применяют почти во всех машинах (болты, валы, муфты, механические передачи и т.п.). Эти детали (узлы) называют деталями общего назначения и изучают в курсе «Детали машин».

Редукторы коническо цилиндрические (КЦ) двухступенчатые, предназначены для использования в изделиях подъемно-транспортного оборудования, таких как тали Болгарии и тельферы, а также для ремонтно-эксплуатационных нужд действующего оборудования.

Редуктором коническо цилиндрическим называют механизм, служащий для передачи мощности от электродвигателя к рабочему органу исполнительного устройства. С помощью редукторов осуществляют уменьшение угловой скорости, а также увеличение выходного момента. В зависимости от требуемого расположения геометрических осей валов, между которыми передаётся вращение, и необходимого передаточного числа в редукторах используют цилиндрические, конические, коническо цилиндрические, а также червячные передачи.

Зубчатые коническо цилиндрические редукторы типа КЦ и червячные редукторы характеризуются высокой надежностью, долговечностью, постоянством передаточного числа и простотой в эксплуатации. Такие коническо цилиндрические редукторы имеют малый вес и небольшие габариты при обеспечении больших передаточных чисел.

Для передачи вращательного движения широко используют зубчатые и червячные механизмы. Если геометрические параллельны, то в редукторах коническо цилиндрических применяют цилиндрические зубчатые колеса, если оси валов пересекаются, то конические зубчатые колеса, а при перекрещивающихся осях валов ведущим звеном является червяк, ведомым – червячное колесо. Каждую передачу, состоящую из двух колес, независимо от ее типа называют ступенью.

Для поддержания вращающихся деталей редукторов и передачи крутящих моментов между ними служат валы. От прочности и жесткости валов во многом зависит работоспособность механизмов.

Чтобы уменьшить габариты редуктора в целом, электродвигатель часто устанавливают непосредственно в его корпусе. При этом ведущее колесо первой ступени насаживают непосредственно на вал электродвигателя, поэтому вал электродвигателя одновременно является входным валом редуктора коническо цилиндрического. Такие конструкции принято называть мотор редукторами.

1. Кинематический расчет привода

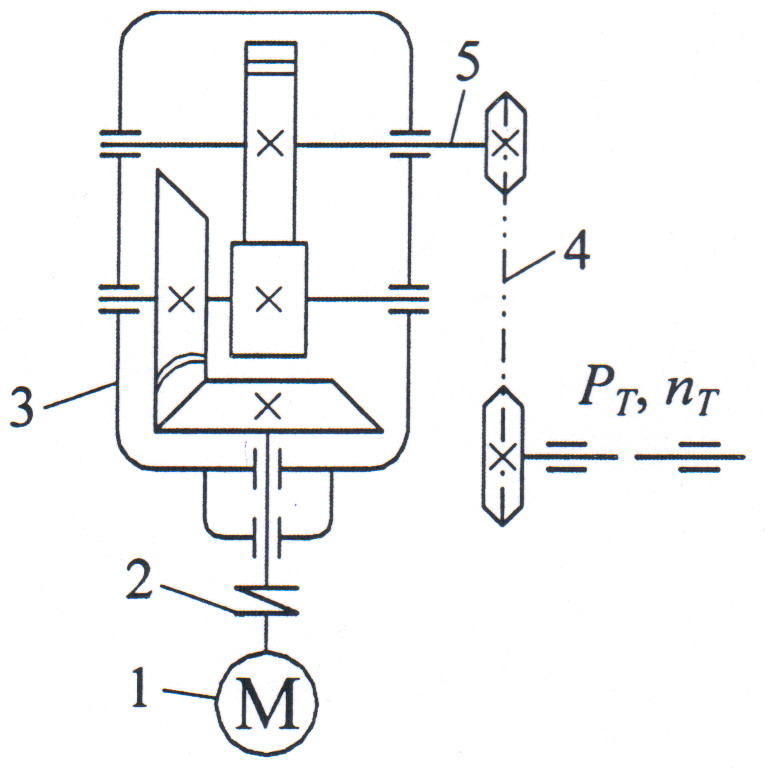
Рисунок 1.1 Кинематический расчет привода.

1 – Электродвигатель;

2 – Муфта упругая;

3 – Редуктор;

4 – Цепная передача;

5 – Выходной вал редуктора.

1. Определяем общий КПД привода по формуле:

_общ = ₁  ₂  ₃  _I

КПД отдельных звеньев кинематической цепи назначаем по таблице П.1 1

_общ = _м  _б  _т  _ц = 0,98  0,96  0,951  0,93 = 0,832,

где _м = 0,98 – КПД упругой муфты; _б = 0,96 – КПД зубчатой передачи быстроходной ступени редуктора; _т = 0,951 – КПД зубчатой передачи тихоходной ступени редуктора;

_ц = 0,93 – КПД цепной передачи.

2. Находим потребную мощность электродвигателя по формуле:

P_эд.р = P_Т/_общ = 2,6/0,832 = 3,125 кВт.

3. Определяем частоту вращения вала электродвигателя по формуле:

n_эд.р = n_Т  u_пр = 40  25 = 1000 мин^-1

4. По таблице П.8 1 выбираем электродвигатель единой серии АИР:

Тип АИР 112МА6У3; P_эд = 3 кВт; n_эд = 955 мин^-1; Т_пуск/Т_ном = 2,0; m_эд = 35 кг.

5. Определяем расчетное значение общего передаточного числа привода по формуле:

u_общ = n_эд./n_Т = 955/40 = 23,875

6. Принимаем передаточное число цепной передачи по таблице П.3 1:

u_ц = 2

Передаточное число редуктора определяем по формуле:

u_ред = u_общ/u_ц = 23,875/2 = 11,9375

7. Разбиваем u_ред по ступеням (таблица П.13, схема 6 1) u_б = 4;

u_Т = u_ц/ u_б = 11,9375/4 = 2,984375

По таблице П.2 1 округляем полученное значение и_Т до стандартного ближайшего значения: u_Т = 3,15.

Определяем передаточное число быстроходной ступени

u_б = u_ред/ u_Т = 11,9375/3,15  3,79

По таблице П.2 1 округляем полученное значение u_б до стандартного ближайшего значения: u_б = 4.

8. Определяем частоты вращения на валах привода.

Быстроходный вал редуктора:

n_б = n_эд = 955 мин^-1

Промежуточный вал редуктора:

n_П = n_б/u_б = 955/4 = 238,75 мин^-1

Тихоходный вал редуктора:

n_{Т Р} = n_П /u_Т = 238,75/3,15  75,79 мин^-1

Тихоходный вал привода:

n_{Т пр} = n_{Т Р}/u_ц = 75,8/2  37,9 мин^-1

Отклонение фактической частоты вращения тихоходного вала привода n_{Т пр} от заданного значения n_Т:

n = ( n_Т – n_{Т пр})/ n_Т100% = ( 40 – 37,9)/ 40100% = 5,26%.

9. Определяем вращающие моменты на валах привода по формуле:

Т_i = 9550P_i/n_i

Быстроходный вал редуктора:

Т_б = 9550P_б/n_б = 9550  2,94/955 = 29,4 Нм,

где P_б = P_эд.р  _м = 3  0,98 = 2,94 кВт; n_б = 955 мин^-1

Промежуточный вал редуктора:

Т_П = 9550P_П/n_П = 9550  2,822/238,75 = 112,9 Нм,

где P_П = P_б  _б = 2,94  0,96 = 2,822 кВт; n_П = 238,75 мин^-1

Тихоходный вал редуктора:

Т_Т= 9550P_Т/n_Т = 9550  2,684/75,79 = 338,2 Нм,

где P_Т = P_П _Т = 2,85  0,951 = 2,684 кВт; n_{Т Р}  75,79 мин^-1

Тихоходный вал привода:

Т_{Т пр}= 9550P_Тпр /n_Тпр = 9550  2,496/37,9 = 629 Нм,

где P_Тпр = P_Т _ц = 2,684  0,93 = 2,496 кВт; n_Тпр = 37,9 мин^-1

2. Расчет цилиндрической зубчатой передачи

1. Исходные данные

Шестерня – Z1	Колесо – Z2
n1 = 238,8 мин-1 Т1 = 112,9 Нм	n2 = 75,8 мин-1 Т2 = 338,2 Нм
(uТ = 3,15)

–передача закрытая, реверсивная;

–срок службы L = 5 лет, коэффициенты использования: К_сут = 0,67, К_год = 0,67;

–режим нагружения: типовой 3 – средний нормальный;

–производство передачи – крупносерийное.

Z₂

Z₁

Рисунок 3.1 Расчетная схема зубчатой передачи.

2. Выбор материалов и расчет допускаемых напряжений

Из таблицы П.1 2 выбираем марку стали, вид термообработки и допускаемые напряжения.

Шестерня – Z1	Колесо – Z2
сталь 20Х т.о цементация и закалка = 59 HRC, Dпред = 120 мм Т = 400 МПа	сталь 40Х т.о закалка ТВЧ (m3 мм) = 48 HRC, Dпред = 200 мм Т = 750 МПа

Необходимо обеспечить:  + (10…15)НВ;

t_ = L  365  К_год  24  К_сут;

N = 60  n  c  t_,

где t_ – суммарное время работы передачи в часах;

n – частота вращения зубчатого колеса, мин^-1;

c – число зацеплений за один оборот, c = 1;

N – число циклов нагружения.

t_ = 5  365  0,67  24  0,67 = 19662 часов

Шестерня – Z1	Колесо – Z2
N1 = 60  238,8  1  19662 = 2,817108 циклов	N2 = 60  75,8  1  19662 = 8,941107 циклов

N_НЕ = K_НЕ  N,

где N_НЕ – эквивалентное число циклов нагружения;

K_НЕ – коэффициент, выбираемый по таблице П.2 2 K_НЕ = 0,18

Шестерня – Z1	Колесо – Z2
NНЕ1 = 0,18  2,817108 = 5,07107 циклов	NНЕ2 = 0,18 8,941107 = 1,609107 циклов

Базовое число циклов N_НО зависит от твердости поверхности зуба:

т.о. цементация и закалка N_НО = 1,210⁸–const при  57 HRC; т.о. закалка ТВЧ N_НО = 2500 ( =35…56 HRC).

Шестерня – Z1	Колесо – Z2
NНО1 = 1,2108 циклов	NНО2 = 2500  482,65 = 7,132107 циклов

,

где K_HL – коэффициент долговечности, причем: 1 K_HL 2,4

Шестерня – Z1	Колесо – Z2
1,154	1,282

_Н = _Н₀  K_HL,

где _Н – допускаемое контактное напряжение с учетом K_HL  1, МПа;

_Н₀ – допускаемое контактное напряжение для K_HL = 1, МПа, определяется из таблицы П.1 2.

Шестерня – Z1	Колесо – Z2
Н1 = Н01  KHL1 = 1131  1,154 = = 1305,7 МПа	Н2 = Н02  KHL2 = 847  1,282 = = 1085,5 МПа

В качестве допускаемого напряжения _Н выбирается меньшее из двух значений (согласно стандарту) _Н = 1085 МПа.

N_FE = K_FE  N,

где N_FE – эквивалентное число циклов нагружения (по изгибу);

K_FE – коэффициент, выбранный по таблице П.2 2 и рисунке П.1 2.

K_FE = 0,04.

Шестерня – Z1	Колесо – Z2
NFЕ1 = 0,04  2,817108 = 1,127107 циклов	NFЕ2 = 0,04  8,941107 = 3,577106 циклов

Базовое число циклов N_F0 = 0,4  10⁷ для всех сталей.

,

где K_FL – коэффициент долговечности (по изгибу);

m_F = 6 – для зубчатых колес со шлифованной переходной поверхностью.

Шестерня – Z1	Колесо – Z2
1

_F = _F₀  K_FL  K_FC.

где _F – допускаемое напряжение изгиба, МПа;

_F₀ – допускаемое напряжение изгиба, МПа, при K_FL = 1 и K_FC = 1 определяется из таблицы П.1 2;

K_FC – коэффициент, равный 0,75 для реверсивной передачи.

K_FC = 0,75

Шестерня – Z1	Колесо – Z2
F1 = F01  KFL1  KFC = 500  1  0,75 = =375 МПа	F2 = F02  KFL2  KFC = 371  1  0,75 = 278 МПа

Предельные допустимые напряжения для кратковременной (пиковой) перегрузки (таблица П.1 2):

Шестерня – Z1	Колесо – Z2
H1max = 2360 МПа F1max = 1200 МПа	H2max = 1920 МПа F2max = 1260 МПа

3. Проектный расчет зубчатой передачи.

,

где а_W – межосевое расстояние, мм;

E_пр – приведенный модуль упругости, E_пр = 2,110⁵ МПа;

T₂ – вращающий момент на колесе, Нм;

K_H – коэффициент, учитывающий концентрацию нагрузки;

u – передаточное число;

_ba – коэффициент ширины зуба относительно межосевого расстояния: _ba = b_W/а_W.

Согласно таблице П.3 выбираем _ba = 0,2.

Для схемы 4 (рисунок П.3 2) из ряда чисел (таблица П.4 2) несимметричное расположение и  350 HB 2–я ступень: _ba  0,21,25 = 0,25,

_bd = 0,50,25(3,15+1)  0,519.

Согласно таблице П.5 2 находим K_H:

,

(_bd)_пред = 1,4.

_bd = 0,519  (_bd)_пред = 1,4.

1,106.

Подставляя _bа, K_H и другие значения в формулу для расчета а_W, находим:

105,7 мм,

принимаем а_W = 105 мм (из ряда R_a 40 таблица П.4 2)

b_W = _ba а_W,

где b_W – рабочая ширина зубчатого венца шестерни, мм;

b_W = 0,25105 = 26,25 мм.

Принимаем b_W = 27 мм

Выбор модуля (рисунок П.2 2): – для и  350 HB

3,281…1,667,

принимаем m = 2,5 мм.

Выбираем такое число из стандартного ряда (таблица П.4 2), при котором Z_ = Z₁ + Z₂:

.

=84;

.

= 20,241.

Округляем: Z₁ = 20  Z_min = 17,

Z₁ = 20 зубьев.

Для внешнего зацепления: Z₂ = Z_ – Z₁ u_ф = Z₂/Z₁; d₁ = mZ₁; d₂ = mZ₂.

Z₂ = 84 – 20 = 64 зуб,

u_ф = 64/20 = 3,2.

Расхождение: =1,587%.

d₁ = 2,520 = 50 мм,

d₂ = 2,564 = 160 мм.

Найденные значения сопоставляем с предельными диаметрами заготовок D_пред из таблицы П.1 2. Необходимо обеспечить:

d  D_пред:

d₁ = 50 мм  D_пред = 120 мм,

d₂ = 160 мм  D_пред = 200 мм.

4. Проверка выполнения условий прочности

   1. Условие прочности по контактным напряжениям

,

где – контактное напряжение, МПа;

T_l = 112,9 Нм – вращающий момент на шестерне;

d_Wl – начальный диаметр шестерни, мм. Для передач без смещения и с x_ = 0, d_Wl = d_l = 50 мм;

_W – угол зацепления, для передач X_ = 0, _W = 20;

K_H – коэффициент расчетной нагрузки, причем: K_H = K_H K_HV;

K_HV – коэффициент динамичной нагрузки, определяемый по формулам из таблицы П.7 2.

K_HV = 1+0,035 – для и  350 HB и  = 0,

где  – окружная скорость колеса, м/с:

.

По таблице П6 2 определяем степень точности передачи:

 0,635 м/с.

Степень точности – девятая.

K_HV = 1+0,035 = 1+0,0350,635  1,022,

K_H = K_H  K_HV = 1,106  1,022  1,131.

Находим величину контактного напряжения:

1063 МПа.

Так как 1063 МПа < 1085 МПа, то производить коррекцию не требуется.

2. Условие прочности по напряжениям изгиба

,

где Y_F = 3,75 – коэффициент формы зуба, определяем по формуле из таблицы П.8 2;

– окружная сила на колесе, Н.

 4227 Н.

K_F – коэффициент расчетной нагрузки, причем:

K_F = K_F  K_FV.

Формулы для расчета K_F и K_FV находим из таблиц П.9 и П.7 2.

K_F = 1+0,39  = 1+0,39  0,519^1,59  1,137,

K_FV = 1+0,035   = 1+0,035  0,635  1,022.

Тогда

K_F = 1,137  1,022 = 1,163.

Находим отношение _F / Y_F:

Шестерня – Z1	Колесо – Z2
375 / 3,75 = 100	278 / 3,75 = 74,2

Так как 74,2  100 то, расчет ведем по «колесу».

Действующее напряжение изгиба:

 273 МПа.

3. Расчет на заданную (пиковую) перегрузку

_{H max} = _H   _H _max,

_{F max} = _F  K _O  _F _max,

где 2,126,

Т_пуск, Т_ном – пусковой и номинальный вращающие моменты электродвигателя привода,

P_эд, P_П – мощность двигателя по каталогу и мощность на промежуточном валу редуктора.

_{H max} = 1063  = 1549 МПа < _H _max = 1920 МПа,

_{F max} = 273  2,126 = 580 МПа  _F _max = 1260 МПа.