7.4. Задания и ответы

Сфера производства некоторой экономической системы состоит из двух отраслей. Найти оптимальный режим работы этих отраслей, обеспечивающих структуру прибавочного продукта, заданного столбцом с, при условии, что матрица материальных затрат А и строка рабочей силы 1 имеют следующий вид:

1. 

и известно, что мощность первой отрасли не превосходит 24, мощность второй отрасли не превосходит 12, а общее число рабочих L равно 120;

2. 

и известно, что мощность первой отрасли не превосходит 6, мощность второй отрасли не превосходит 12, а общее число рабочих L равно 90;

3. 

и известно, что мощность первой отрасли не превосходит 20, мощность второй отрасли не превосходит 11, а общее число рабочих L равно 72;

b₂x₁ = b₁x₂.

Полученное равенство на плоскости (x₁, x₂) описывает прямую, проходящую через начальную точку 0(0,0).

В свою очередь, неравенства (2) можно проиллюстрировать так, как показано на рис. 2.

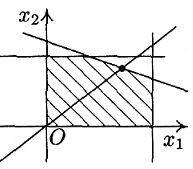
Рис. 2

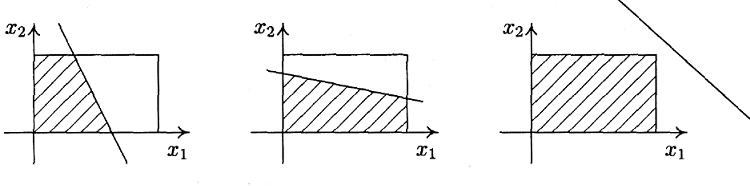
Рис. 3

На рис. 3 представлены все возможные случаи.

Замечание. На рис. 2 жирная точка отвечает α_max.

4. 

и известно, что мощность первой отрасли не превосходит 12, мощность второй отрасли не превосходит 8, а общее число рабочих L равно 96;

Ответы:

1) х₁ = 14, х₂ = 12, α_max = 1/2;

2) х₁ = 8, х₂ = 8, α_max = 1/3;

3) х₁ = 20, х₂ = 10, α_max = 3/12;

4) х₁ = 12, х₂ = 8, α_max = 2/3.

Глава 8 многокритериальные задачи

В рассматриваемой выше задаче линейного программирования мы сталкивались с ситуацией, когда при известных условиях на числовые параметры требовались найти наибольшее (или наименьшее) значение некоторое заданной целевой функции, которую часто называют критерием. И тогда среди всех возможных наборов неизвестных мы выбрали тот, который обеспечивал бы это искомое экстремальное значение критерия. Однако при решении практических задач нередко приходиться иметь дело с ситуациями, когда необходимо одновременное выполнение нескольких условий (критериев), зачастую противоречивых. Например, в стремлении приобрести товар получше и подешевле покупатель сталкивается с тем, что товар, вполне подходящий по цене, не удовлетворяет по качеству, а высокое качество товара принимает и цену.

Пример 1. Из железного листа, имеющего форму квадрата со стороной l, требуется скроить коробку максимально возможного обьема при минимальном расходе материала.

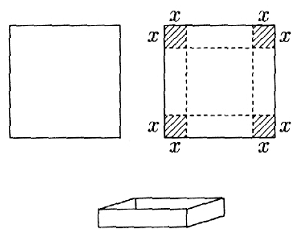
Рис. 1